5.8.4. Расчёт электрической цепи методом контурных токов

При расчёте электрической цепи методом контурных токов в схему вводятся условные токи, протекающие по контуру неизменными. Они обозначены на рис. 5.8.5 символами İ₁₁, İ₂₂ и İ₃₃.

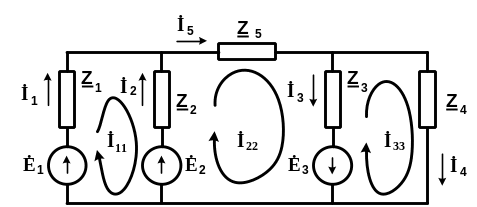
Рис. 5.3.5. Схема электрической цепи для расчёта методом контурных токов

Для контурных токов первый закон Кирхгофа выполняется автоматически. Действительно, для первого узла контурный ток İ₁₁ входит в узел и выходит из него. Аналогично и ток İ₂₂. То есть

– İ₁₁+ İ₁₁ – İ₂₂ + İ₂₂ = 0

Поэтому для контурных токов уравнения составляются только по второму закону Кирхгофа.

В первом контуре ток İ₁₁ протекает по пассивным элементам Z₁ и Z₂. В то же время по Z₂ навстречу току İ₁₁ протекает ток İ₂₂. Следовательно, второй закон Кирхгофа для первого контура имеет вид.

(Z₁ + Z₂) İ₁₁ – Z₂ İ₂₂ = Ė₁ – Ė₂.

По аналогии второй и третий контуры описываются с помощью контурных токов следующими уравнениями.

– Z₂ İ₁₁ + (Z₂ + Z₅ + Z₃)İ₂₂ – Z₃ İ₃₃= Ė₂ + Ė₃,

– Z₃ İ₂₂ + (Z₃ + Z₄)İ₃₃ = – Ė₃.

В результате решения системы из трёх уравнений для всех контуров имеем контурные токи İ₁₁, İ₂₂ и İ₃₃. Действительные токи İ₁, İ₂, İ₃, İ₄ и İ₅ определяются через контурные, с помощью схемы рис. 5.3.5. По первой ветви протекает действительный ток İ₁ и в том же направлении только один контурный ток İ₁₁. Следовательно,

İ₁ = İ₁₁.

По второй ветви согласно с действительным током İ₂ протекает контурный ток İ₂₂ и навстречу контурный ток İ₁₁. Следовательно,

İ₂ = İ₂₂ – İ₁₁.

По аналогии действительные токи в других ветвях определяются через контурные по выражениям.

İ₃ = İ₂₂ – İ₃₃,

İ₄ = İ₃₃,

İ₅ = İ₂₂.

5.8.5. Расчёт электрической цепи методом узловых потенциалов

При расчёте электрической цепи методом узловых потенциалов уравнения составляются для потенциалов узлов электрической цепи. Уравнения получаются из первого закона Кирхгофа. Поэтому количество уравнений при расчёте электрических цепей этим методом равно m –1. Однако, поскольку для расчёта токов необходимы потенциалы всех узлов, потенциал одного из узлов должен быть задан. Чаще всего потенциал одного из узлов принимается равным нулю (узел заземляется).

В электрической цепи рис. 5.3.6 узел 3 заземлён.

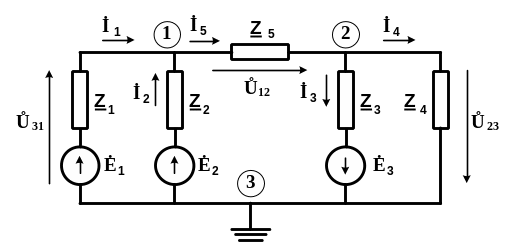
Рис. 5.3.6. Схема электрической цепи для расчёта методом узловых

потенциалов

Для узлов 1 и 2 уравнения имеют вид.

,

.

В результате решения этих уравнений имеем потенциалы узлов и .

Искомые токи определяем по закону Ома. В первой ветви ток протекает от узла 3 к узлу 1. Согласно с током İ₁ действует напряжение Ů₃₁ , равное разности потенциалов и , и ЭДС источника Ė₁. Поэтому, с учётом того, что

İ₁= .

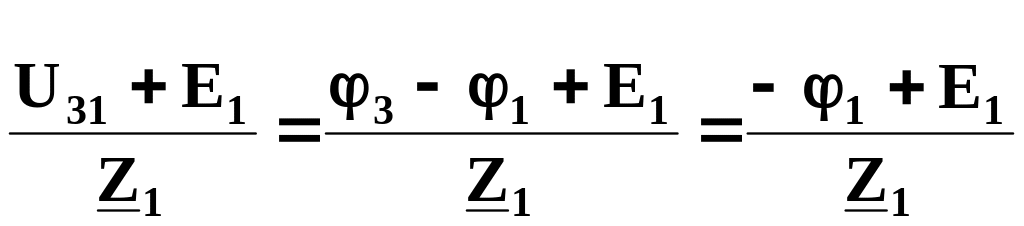По аналогии остальные токи определяются выражениями

İ₂ = ,

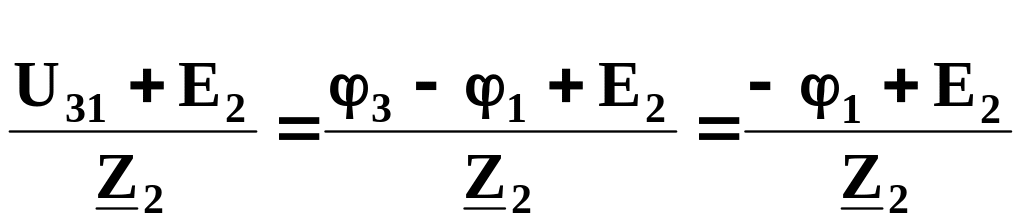İ₃ = ,

İ₄ = ,

İ₅ = .

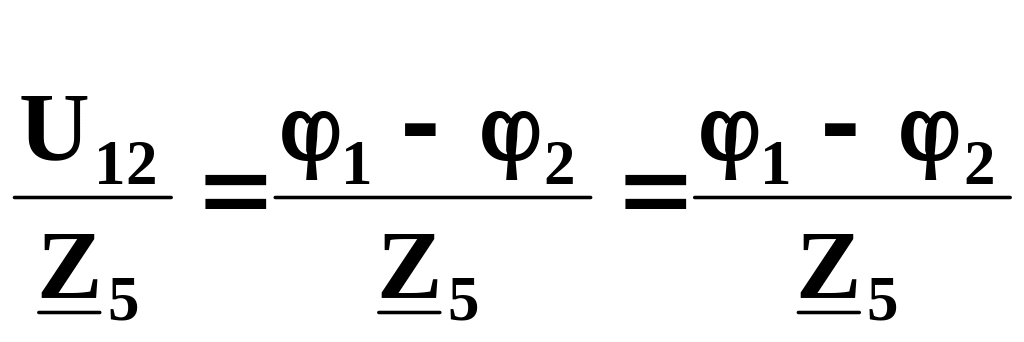Таким образом, расчёт токов электрической цепи можно выполнять различными методами. При этом важно выбирать оптимальный, исходя из постановки задачи расчёта, структуры рассчитываемой цепи, известных данных и других особенностей. В дальнейшем, на основе рассчитанных токов, можно определить напряжения на элементах электрической цепи, потребляемые ими мощности и другие интересующие величины.