Тема 3: Моменты распределения. Асимметрия и эксцесс.

Моментом распределения называется средняя ве­личина отклонений определенной степени от какого-либо числа. Если это число - средняя арифметическая, то моменты называются цент­ральными. Если отклонения отсчитываются от произвольно выб­ранного начала, то они называются условными. Если же это число равно нулю, то моменты распределения называются начальными.

Формула момента распределения имеет вид:

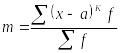
На основе момента третьего порядка можно построить показа­тель, характеризующий степень асимметричности распределения, который называют коэффициентом асимметрии As.

Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений п и рассчитывается по формуле:

Если отношение , асимметрия существенна, а если , несущественна, ее наличие может быть объяснено влиянием раз­личных обстоятельств.

Английский статистик К. Пирсон на основе разности между средней величиной и модой предложил другой показатель – коэффициент асимметрии Пирсона:

При симметричном (нормальном) распределении , сле­довательно, коэффициент асимметрии равен нулю. Если Аs > 0, то имеется правосторонняя асиммет­рия. Если As < 0, то - ле­восторонняя асимметрия.

С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом.

Часто эксцесс интерпретируется как «крутизна» или «островершинность» распределения. При симметричном распределении Ех = 0. Если Ех > 0, рас­пределение является островершинным; если Eх < 0 - плосковер­шинным.

Задача 36.

По приведенному ниже ряду распределения требуется выполнить следующие задания:

1. Рассчитать среднее значение признака, моду, медиану;

2. Вычислить показатели асимметрии и эксцесса.

Сформулировать выводы.

Распределение автомобилей по величине межремонтного пробега

Величина межремонтного пробега, тыс.км	Число автомобилей
80 – 100	10
100 – 120	60
120 – 140	100
140 – 160	26
160 – 180	14
Итого	210

Тема 5: Выравнивание вариационных рядов (построение теоретических распределений).

Наиболее часто используются законы распределения нормальный и Пуассона.

График нормального распределения имеет форму колоколообразной кривой, симметричной относительно , концы которой асимптотически приближаются к оси абсцисс. Она имеет точки перегиба, абсциссы которых находятся на расстоянии  от центра симметрии. Эта кривая выражается уравнением:

где у – ордината кривой нормального распределения;

- нормированные отклонения.

При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяются по формуле

где N= f – сумма всех частот вариационного ряда;

h – величина интервала в группах (классах);

 - среднее квадратическое отклонение;

- нормированное отклонение вариантов от средней арифметической.

Значение ординат кривой нормального распределения будет соответствовать величине , которая табулирована и определяется по таблицам значений данной функции (t) (приложение 1).

Распределение Пуассона. В целом ряде случаев, если вариационный ряд представляет собой распределение по дискретному признаку, где по мере увеличения значений признака х частоты резко уменьшаются и где средняя арифметическая ряда равна или близка по значению к дисперсии, т.е. =², то такой ряд можно выровнять по кривой Пуассона, аналитическое выражение которой

где Р_х – вероятность наступления отдельных значений х;

а = – средняя арифметическая ряда.

Теоретические частоты при выравнивании эмпирических данных определяются по формуле:

f’ =N P_x ,

где f ^’- теоретические частоты;

N – общее число единиц ряда.

После выравнивания ряда, т.е. нахождения теоретических частот, возникает необходимость проверить, случайны или существенны расхождения между эмпирическими и теоретическими частотами, и тем самым проверить правильность выдвинутой при выравнивании ряда гипотезы о наличии того или иного характера распределения в эмпирическом ряду.

Для оценки близости эмпирических (f) и теоретических (f ^’ ) частот можно применить один из критериев согласия: критерий Пирсона (² – «хи-квадрат»), критерий Романовского, критерий Колмогорова ( - «лямбда»).

Критерий Пирсона (²) представляет собой сумму отношений квадратов расхождений между f и f ^‘ к теоретическим частотам:

.

Фактическое значение ² сравнивают с критическим, определяемым по специальным таблицам (приложение 2) в зависимости от принимаемого уровня значимости и числа степеней свободы.

Уровень значимости () – вероятность допуска ошибки в утверждении гипотетического закона (характера) распределения – обычно принимается равным 5 % (=0,05).

Число степеней свободы (k) рассчитывается: k = m – 1 – b

Где m – число групп в ряду распределения; b - число параметров эмпирического распределения, использованных для нахождения теоретических частот. Так, при выравнивании по кривой нормального распределения число степеней свободы k = m – 1 – 2, поскольку при расчете теоретических частот используется два параметра эмпирического распределения (b=2: и ), т.е. k = m –3. для закона Пуассона b = 1 (а = )

Если фактическое ² оказывается меньше табличного (критического), то расхождения между эмпирическими и теоретическими частотами можно считать случайными.

Критерием Романовского:

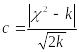
Если указанное отношение меньше 3, то расхождения считают случайными, если больше 3, то они существенны.

Критерий Колмогорова () основан на определении максимального расхождения между накопленными частотами эмпирического и теоретического распределений:

где D – максимальная разность между накопленными частотами ;

N – сумма всех частот.

Далее по таблицам находится Р(λ) (приложение 3). Чем вероятность ближе к 1, тем увереннее мы можем утверждать, что расхождения между частотами случайны.

На основании полученных значений критериев согласия делаются выводы о близости эмпирических и теоретических частот, таким образом, подтверждается или опровергается гипотеза о наличии того или иного характера распределения в эмпирическом ряду.