Экспериментальная часть
I) Анализ рентгенограмм полученных до и после прогрева образца.
Расчет шел по двум направлениям:
а) Исследование углового положения – дает возможность определять межплоскостные расстояния d и параметры элементарной ячейки. Так же фиксировать изменение геометрических размеров от различных условий.
1) Определение межплоскостных расстояний.
До прогрева:
№ |
2ϴ |
ϴрадиан |
d |
l1 |
l2 |
l3 |
λ =1,54178 |
3 |
0,026167 |
29,46413 |
29,46413 |
|
|
|
4,4 |
0,038378 |
20,09182 |
|
20,09182 |
|
|
8,8 |
0,076756 |
10,05331 |
3,0 |
2,0 |
10,05331 |
|
13,05 |
0,113825 |
6,787236 |
4,0 |
3,0 |
|
|
17,7 |
0,154383 |
5,013241 |
6,0 |
4,0 |
2,0 |
|
22,21 |
0,193721 |
4,004391 |
|
5,0 |
|
λ1=1,54051 |
26,68 |
0,232709 |
3,340015 |
9,0 |
6,0 |
3,0 |
|
31,38 |
0,273703 |
2,849643 |
10,0 |
7,0 |
|
|
35,77 |
0,311994 |
2,509326 |
12,0 |
8,0 |
4,0 |
|
45,13 |
0,393634 |
2,008242 |
15,0 |
10,0 |
5,0 |
|
54,88 |
0,478676 |
1,672272 |
18,0 |
12,0 |
6,0 |
|
65,01 |
0,567032 |
1,434018 |
21,0 |
14,0 |
7,0 |
|
75,73 |
0,660534 |
1,255431 |
24,0 |
16,0 |
8,0 |
|
87,37 |
0,762061 |
1,115643 |
27,0 |
18,0 |
9,0 |
|
100,22 |
0,874141 |
1,004253 |
30,0 |
20,0 |
10,0 |
|
115,61 |
1,008376 |
0,910502 |
33,0 |
22,0 |
11,0 |
|
134,12 |
1,169824 |
0,836613 |
36,0 |
24,0 |
12,0 |
Зная из рентгенограммы углы, соответствующие пикам интенсивности, находили d из уравнения Вульфа-Брэгга (λ-длинна волны излучения):
d = λ/(2sinθ)
Определили кратные отражения ln (выбрали только те, где ln принимает целочисленные значения)
l1=d1/ d2, l1=d1/ d3, … l1=d1/ d17;
l2=d2/ d3, l2=d2/ d4, … l2=d2/ d17;
l3=d3/ d4, l3=d3/ d5, … l3=d3/ d17;
Установлено, что в образце присутствуют 3 отражения разных фаз (30-ти, 20-ти и 10-тиангстремник). 10-тиангстремник является основной фазой, входящей в остальные отражения.
После прогрева:
№ |
2ϴ |
ϴрадиан |
d |
l1 |
l2 |
l3 |
Прогрев |
4,52 |
0,039424 |
19,55867 |
|
1,0 |
|
λ |
8,9 |
0,077628 |
9,940575 |
3,0 |
2,0 |
1,0 |
|
13,36 |
0,116529 |
6,630437 |
|
3,0 |
|
|
17,7 |
0,154383 |
5,013241 |
|
4,0 |
2,0 |
|
21,25 |
0,185347 |
4,183076 |
7,0 |
|
|
|
26,72 |
0,233058 |
3,337855 |
|
6,0 |
3,0 |
λ 1 |
35,86 |
0,312779 |
2,503235 |
|
8,0 |
4,0 |
|
44,5 |
0,388139 |
2,0352 |
|
|
|
|
45,25 |
0,394681 |
2,003195 |
|
10,0 |
5,0 |
|
54,98 |
0,479548 |
1,669466 |
|
12,0 |
6,0 |
|
64,85 |
0,565636 |
1,437169 |
|
14,0 |
7,0 |
|
65,15 |
0,568253 |
1,431274 |
|
14,0 |
7,0 |
|
75,93 |
0,662278 |
1,25262 |
|
16,0 |
8,0 |
|
81,9 |
0,71435 |
1,175735 |
|
17,1 |
8,6 |
|
87,58 |
0,763892 |
1,113508 |
|
18,0 |
9,0 |
|
98,4 |
0,858267 |
1,017899 |
29,0 |
|
|
|
100,51 |
0,876671 |
1,002136 |
|
20,0 |
10,0 |
|
115,47 |
1,007155 |
0,911204 |
|
22,0 |
11,0 |
|
134,55 |
1,173575 |
0,835291 |
|
|
12,0 |
Из данных после прогрева видно, что 30-тиангстремник полностью исчез (нет первого отражения), 20-тиангстремник потерял некоторые отражения, следственно эти 2 фазы являлись примесными. Полностью сохранил все свои кратные отражения 10-тиангстремник, который является основной фазой. Следовательно, далее в работе будет рассматриваться только эта фаза.
Проведем анализ погрешности определения межплоскостных расстояний.
∆d |
0,176394 |
0,087857 |
0,058185 |
0,043220 |
0,034127 |
0,027958 |
0,023445 |
0,019952 |
θ |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
∆θ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
d |
8,842156 |
4,437948735 |
2,977512 |
2,25317 |
1,823444 |
1,541219 |
1,343493 |
1,19881 |
θрад |
0,087222 |
0,174444444 |
0,261667 |
0,348889 |
0,436111 |
0,523333 |
0,610556 |
0,697778 |
∆θрад |
0,001744 |
0,003488889 |
0,005233 |
0,006978 |
0,008722 |
0,010467 |
0,012211 |
0,013956 |
∆d |
0,017123 |
0,014736783 |
0,012652 |
0,010766 |
0,009003 |
0,007302 |
0,005607 |
0,003866 |
θ |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
∆θ |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
d |
1,089739 |
1,00586999 |
0,940628 |
0,889687 |
0,85011 |
0,819873 |
0,797569 |
0,782235 |
θрад |
0,785 |
0,872222222 |
0,959444 |
1,046667 |
1,133889 |
1,221111 |
1,308333 |
1,395556 |
∆θрад |
0,0157 |
0,017444444 |
0,019189 |
0,020933 |
0,022678 |
0,024422 |
0,026167 |
0,027911 |
∆d |
0,002024 |
0,000019 |
|
|
|
|
|
|
θ |
85 |
90 |
|
|
|
|
|
|
∆θ |
1,7 |
1,8 |
|
|
|
|
|
|
d |
0,773248 |
0,770255244 |
|
|
|
|
|
|
θрад |
1,482778 |
1,57 |
|
|
|
|
|
|
∆θрад |
0,029656 |
0,0314 |
|
|
|
|
|
|
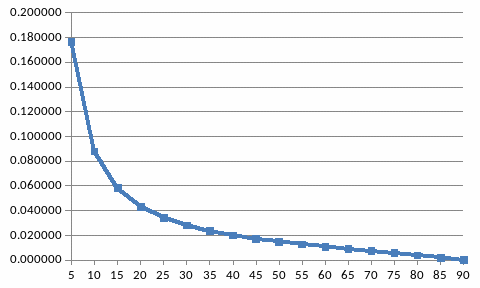
И з графика видно, что минимальная погрешность у нас будет при θ=900
3) Определение параметров элементарной ячейки.
Для определения параметров элементарной ячейки необходимо провести экстраполяцию экспериментальных данных С, полученных по рентгенограмме на угле θ=900
Для 30-тиангстремника С1=d*l1, f(exp)=0,5*(Ctg2(θ)+cos2(θ)/θ)
d1 |
L1 |
C1 |
θ |
f(exp) |
1,0 |
29,46413 |
29,46413 |
0,026167 |
749,01464 |
3,0 |
10,05331 |
30,15993 |
0,076756 |
91,01200 |
4,0 |
6,787236 |
27,14894 |
0,113825 |
42,59491 |
6,0 |
5,013241 |
30,07944 |
0,154383 |
23,80782 |
9,0 |
3,340015 |
30,06013 |
0,232709 |
10,93585 |
10,0 |
2,849643 |
28,49643 |
0,273703 |
8,03688 |
12,0 |
2,509326 |
30,11192 |
0,311994 |
6,25818 |
15,0 |
2,008242 |
30,12363 |
0,393634 |
3,98221 |
18,0 |
1,672272 |
30,10089 |
0,478676 |
2,67970 |
21,0 |
1,434018 |
30,11438 |
0,567032 |
1,86043 |
24,0 |
1,255431 |
30,13033 |
0,660534 |
1,30029 |
27,0 |
1,115643 |
30,12236 |
0,762061 |
0,89231 |
30,0 |
1,004253 |
30,1276 |
0,874141 |
0,58544 |
33,0 |
0,910502 |
30,04658 |
1,008376 |
0,33964 |
36,0 |
0,836613 |
30,11808 |
1,169824 |
0,15498 |
|
|
30,11808 |
1,221111 |
0,11455 |
|
|
30,11808 |
1,395556 |
0,02656 |
|
|
30,11808 |
1,57 |
0,00000 |
Для точного определения график был продлен до угла θ=900 (угол был переведен в радианы) т.к. там будет минимальная погрешность. Из графика находим параметр элементарной ячейки С1=30,11808
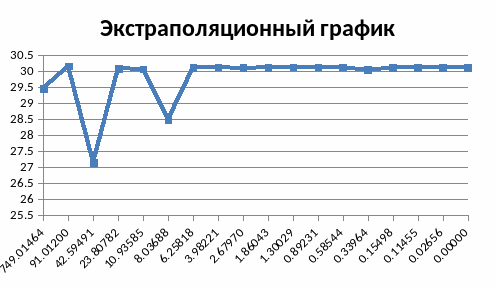
Для 20-тиангстремника С2=d*l2=20,09182 (предпоследнюю точку можно считать выпавшей).
d2 |
L2 |
C2 |
θ |
f(exp) |
1,0 |
20,09182 |
20,09182 |
0,038378 |
352,1529 |
2,0 |
10,05331 |
20,09182 |
0,076756 |
91,012 |
3,0 |
6,787236 |
20,09182 |
0,113825 |
42,59491 |
4,0 |
5,013241 |
20,09182 |
0,154383 |
23,80782 |
5,0 |
4,004391 |
20,09182 |
0,193721 |
15,47682 |
6,0 |
3,340015 |
20,09182 |
0,232709 |
10,93585 |
7,0 |
2,849643 |
19,9475 |
0,273703 |
8,036884 |
8,0 |
2,509326 |
20,09182 |
0,311994 |
6,258182 |
10,0 |
2,008242 |
20,09182 |
0,393634 |
3,982215 |
12,0 |
1,672272 |
20,09182 |
0,478676 |
2,679697 |
14,0 |
1,434018 |
20,09182 |
0,567032 |
1,860428 |
16,0 |
1,255431 |
20,09182 |
0,660534 |
1,30029 |
18,0 |
1,115643 |
20,09182 |
0,762061 |
0,892306 |
20,0 |
1,004253 |
20,09182 |
0,874141 |
0,58544 |
22,0 |
0,910502 |
20,03105 |
1,008376 |
0,339644 |
24,0 |
0,836613 |
20,09182 |
1,169824 |
0,154977 |
Для 10-тиангстремника С3=d*l3= 10,05331
d3 |
L3 |
C3 |
θ |
f(exp) |
1,0 |
10,05331 |
10,05331 |
0,076756 |
91,011997 |
2,0 |
5,013241 |
10,05331 |
0,154383 |
23,807822 |
3,0 |
3,340015 |
10,05331 |
0,232709 |
10,935851 |
4,0 |
2,509326 |
10,05331 |
0,311994 |
6,258182 |
5,0 |
2,008242 |
10,05331 |
0,393634 |
3,982215 |
6,0 |
1,672272 |
10,05331 |
0,478676 |
2,679697 |
7,0 |
1,434018 |
10,05331 |
0,567032 |
1,860428 |
8,0 |
1,255431 |
10,05331 |
0,660534 |
1,300290 |
9,0 |
1,115643 |
10,05331 |
0,762061 |
0,892306 |
10,0 |
1,004253 |
10,05331 |
0,874141 |
0,585440 |
11,0 |
0,910502 |
10,05331 |
1,008376 |
0,339644 |
12,0 |
0,836613 |
10,05331 |
1,169824 |
0,154977 |
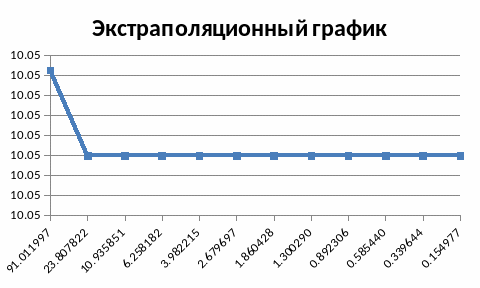
После прогрева
d3 |
L3 |
C3 |
θ |
f(exp) |
1,0 |
9,940575 |
9,940575 |
0,077628 |
89,041916 |
2,0 |
5,013241 |
10,05331 |
0,154383 |
23,807822 |
3,0 |
3,337855 |
10,04681 |
0,233058 |
10,904852 |
4,0 |
2,503235 |
10,0289 |
0,312779 |
6,228070 |
5,0 |
2,003195 |
10,02804 |
0,394681 |
3,961338 |
6,0 |
1,669466 |
10,03644 |
0,479548 |
2,669556 |
7,0 |
1,431274 |
10,03408 |
0,568253 |
1,851481 |
8,0 |
1,25262 |
10,0308 |
0,662278 |
1,291829 |
9,0 |
1,113508 |
10,03407 |
0,763892 |
0,886274 |
10,0 |
1,002136 |
10,03211 |
0,876671 |
0,579761 |
11,0 |
0,911204 |
10,06106 |
1,007155 |
0,341440 |
12,0 |
0,835291 |
10,03742 |
1,173575 |
0,151761 |
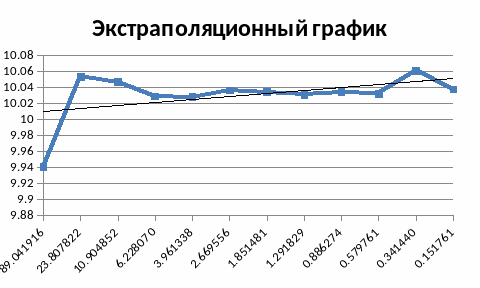
После прогрева наблюдается уменьшение параметра С3, следовательно образовалась фаза отличная от исходной.
б) Исследование интенсивностей - дает возможность построить проекции электронной плотности, определив значения структурных амплитуд из экспериментальных интенсивностей дифракционных отражений. Следовательно, можно определить координаты атомов, а также отследить изменение структуры после нагрева.
По методу Стьюдента оценим погрешность определения минимальной и максимальной интенсивностей. Это необходимо сделать, т.к. для расчета электронной плотности нам необходимо будет найти структурные амплитуды, зависящие от интенсивности.
Ii |
Icp |
Ii-Icp. |
(Ii –Iср )2 |
∑(Ii –Iср )2 |
Slср |
Погрешн.= |
max |
|
|
|
|
|
(Slср/ Icp)*100 |
91246 |
90945 |
301 |
90601 |
170486 |
291,964 |
0,321034 |
90926 |
|
-19 |
361 |
|
|
|
90663 |
|
-282 |
79524 |
|
|
|
min |
|
|
|
|
|
|
3719 |
3705 |
14 |
196 |
302 |
12,28821 |
0,331665 |
3700 |
|
-5 |
25 |
|
|
|
3696 |
|
-9 |
81 |
|
|
|
Slср =(∑(Ii –Iср )2/2)^0,5
Из приведенных расчетов видно, что погрешность в определении экспериментальных интенсивностей мала. Следовательно, при расчете электронных плотностей мы получим достоверные значения.
До нагрева
№ |
2ϴ |
ϴрадиан |
plg |
F |
λ=1,54178 |
3 |
0,026167 |
19,10392 |
1,815972 |
|
4,4 |
0,038378 |
13,02198 |
7,774078 |
|
8,8 |
0,076756 |
6,501389 |
118,4688 |
|
13,05 |
0,113825 |
4,373721 |
11,73202 |
|
17,7 |
0,154383 |
3,21292 |
47,31568 |
|
22,21 |
0,193721 |
2,54867 |
9,703957 |
λ1=1,54051 |
26,68 |
0,232709 |
2,109682 |
58,67452 |
|
31,38 |
0,273703 |
1,780949 |
4,495992 |
|
35,77 |
0,311994 |
1,550256 |
174,2546 |
|
45,13 |
0,393634 |
1,203922 |
250,4645 |
|
54,88 |
0,478676 |
0,963524 |
148,6262 |
|
65,01 |
0,567032 |
0,78519 |
178,5574 |
|
75,73 |
0,660534 |
0,643533 |
216,0623 |
|
87,37 |
0,762061 |
0,5239 |
84,25371 |
|
100,22 |
0,874141 |
0,418293 |
182,4163 |
|
115,61 |
1,008376 |
0,315163 |
231,7514 |
|
134,12 |
1,169824 |
0,21197 |
199,5302 |
Находим структурные амплитуды по формуле:
F=
,
где
Находим проекцию электронной плотности:
ρ=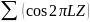
,
где L – индекс Миллера (смена знака у кратных отражений 2 и 5), Z – координаты атомов (0, 0,01, 0,02,…0,51).
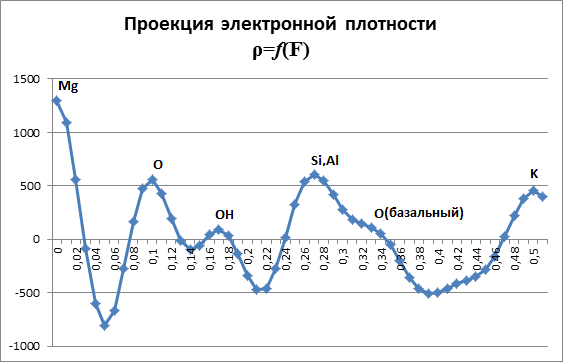
Каждый пик соответствует определенному элементу, или иону, находящемуся в элементарной ячейке.
После прогрева
№ |
2ϴ |
ϴрадиан |
plg |
F |
Прогрев |
4,52 |
0,039424 |
12,67592 |
4,278133 |
λ=1,54178 |
8,9 |
0,077628 |
6,42805 |
168,0614 |
|
13,36 |
0,116529 |
4,271342 |
5,725083 |
|
17,7 |
0,154383 |
3,21292 |
35,93967 |
|
21,25 |
0,185347 |
2,666677 |
7,960826 |
|
26,72 |
0,233058 |
2,106406 |
290,6469 |
λ1=1,54051 |
35,86 |
0,312779 |
1,5461 |
110,4582 |
|
44,5 |
0,388139 |
1,22285 |
18,01809 |
|
45,25 |
0,394681 |
1,200374 |
200,0751 |
|
54,98 |
0,479548 |
0,961472 |
64,3631 |
|
64,85 |
0,565636 |
0,787614 |
13,14053 |
|
65,15 |
0,568253 |
0,783078 |
69,20113 |
|
75,93 |
0,662278 |
0,641221 |
77,0931 |
|
81,9 |
0,71435 |
0,576621 |
13,16906 |
|
87,58 |
0,763892 |
0,521982 |
24,25166 |
|
98,4 |
0,858267 |
0,431968 |
8,333638 |
|
100,51 |
0,876671 |
0,416148 |
48,22961 |
|
115,47 |
1,007155 |
0,316017 |
60,48167 |
|
134,55 |
1,173575 |
0,209761 |
40,8481 |
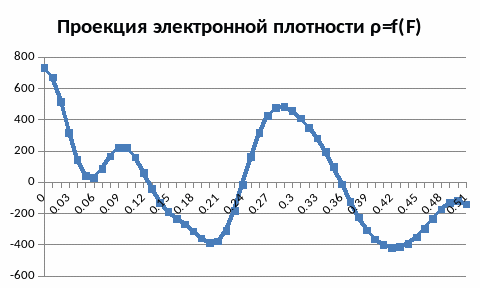
Сравним проекции «до» и «после» прогрева:
После прогрева в октаэдрическом слое структуры произошли изменения обусловленные термической деструкцией групп ОН. Кроме этого наблюдается смещение пиков Si,Al. Механизм этого процесса требует дополнительного исследования.
Соотношение ρ(K)/ρ(Si,Al) уменьшилось в 2,25раза (ρ(K)/ρ(Si,Al) =0,9 «до» прогрева ρ(K)/ρ(Si,Al)=0,4 «после» прогрева). Т.к. из-за отсутствия OH произошли изменения в кристаллической решетке (искажение структуры) в результате чего пик О сгладился.