Температурная рентгенография

Задачей рентгеновской дилатометрии является измерение теплового расширения кристаллов методами температурной рентгенографии.

Процессы, происходящие в кристаллах при нагревании, приводят к существенным термическим деформациям и вызывают тепловое расширение объектов.

Тепловое расширение большинства кристаллов анизотропно и описывается с помощью тензора теплового расширения . При однородном нагревании или охлаждении кристалла тензор термических деформаций связан с тензором теплового расширения следующим соотношением

.

Число независимых компонент тензора теплового расширения определяется сингонией кристалла и равно единице для кубических кристаллов, двум – для одноосных (тетрагональных и гексагональных) и трем – для ромбических кристаллов. Для определения тензора теплового расширения кроме трех главных КТР необходимо задать ориентацию главных осей. В общем случае принято представлять тензор теплового расширения характеристической поверхностью второго порядка 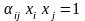, радиусы-векторы которой равны абсолютным значениям КТР по соответствующим направлениям.

В обычных дилатометрических измерениях коэффициент теплового расширения определяется по формуле

, (1)

где – длина кристалла при температуре , – изменение размера кристалла при изменении его температуры на .

Метрической величиной, определяемой из рентгенограмм, являются межплоскостные расстояния , для расчета которых применяется формула Вульфа-Брэгга

. (2)

Дифференцируя (1) по температуре и преобразуя, можно получить выражение для расчета КТР кристалла по выбранному направлению, обозначим его , при определении его рентгеновским методом:

, (3)

где 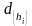− межплоскостное расстояние, − дифракционный угол, − длина волны рентгеновского излучения. Учитывая, что не зависит от температуры, получим для КТР выражение

. (4)

Из выражения (4) следует, что рентгеновский метод позволяет определять КТР кристаллов непосредственно по температурной зависимости дифракционного угла θ без предварительного вычисления межплоскостных расстояний или параметров элементарной ячейки кристаллов для каждой температуры .

Определение размеров кристаллитов и величины микродеформаций

При размерах кристаллитов порядка используется метод измерения уширения интерференционных линий. Метод позволяет определить не только размеры КР, но и оценить величину микродеформаций решетки.

В общем случае ширина и форма линий определяется двумя группами факторов: физических и геометрических. Уширение линий, обусловленное размером кристаллитов и их дроблением на мелкие, разориентированные относительно друг друга блоки, микродеформациями кристаллитов, наличием дефектов упаковки в кристаллитах, называют физическим уширением и обозначают . Геометрические условия регистрации рентгенограммы – сходимость и расходимость первичного пучка, размеры и расположение щелей, собственная ширина спектральной линии характеристического излучения определяют геометрическое или инструментальное уширение. Свой вклад в уширение интерференционного максимума вносят также физические свойства исследуемого образца (поглощение в образце), наложение или неполное разрешение дублета.

Обычно экспериментальная ширина линий обусловлена влиянием всех факторов. Так при наличии в кристалле неоднородной упругой деформации наблюдается закономерное неоднородное изменение межплоскостных расстояний. Вместо строго определенного межплоскостного расстояния d каждая система атомных плоскостей с одинаковыми индексами будет иметь межплоскостные расстояния, лежащие в пределах . Величина микродеформации оценивается по значению относительной деформации 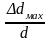. В случае кристаллов кубической сингонии выполняется соотношение .

В результате такого отклонения межплоскостных расстояний от идеальных на величину , для каждой из систем атомных плоскостей углы будут лежать в интервалах значений 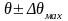. Это приводит к расширению линий на рентгенограмме. Оно тем больше, чем больше будут максимальные значения и .

Чтобы определить размеры кристаллитов, необходимо измерить величину , которую называют истинной шириной интерференционной линии или физическим уширением, исключив влияние геометрических условий. Для этого одновременно с исследуемым образцом получают рентгенограмму эталонного образца, ширина линий которого определяется только геометрическими факторами. Размеры блоков в кристаллитах эталонного образца должны быть больше 1500 , блоки не должны содержать микродеформаций и дефектов упаковки.

Обычно используют обозначения: _– экспериментальная общая ширина линии исследуемого образца; _– то же, для эталона; –истинная общая ширина линии исследуемого образца; – то же, для эталона (истинное геометрическое уширение); – истинное физическое уширение линии исследуемого образца; п – вклад микронапряжений в истинное физическое уширение линии; т – доля истинного физического уширения линии, за которую отвечают размеры блоков мозаики, – относительная микродеформация решетки; – величина блоков мозаики. За величины , , обычно принимают ширину кривой распределения интенсивности на половине высоты, называемую полушириной, или отношение площади интерференционной линии к максимальной высоте. Эти приемы определения ширины идентичны в случае, если профиль имеет треугольника. В этом случае истинное физическое уширение может быть определено как разность между шириной линии исследуемого образца и эталона

. (1)

Применять выражение (1) возможно лишь для случая, когда < .

Если заведомо известно, что истинное физическое уширение линии (hkl) вызвано или исключительно микродеформациями, или только измельчением блоков мозаики до величины, меньшей, чем 1000 , то величина микродеформаций решетки 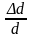в направлении, перпендикулярном плоскости отражения (hkl) и размер блока в направлении, нормальном к (hkl) может быть вычислена по простым формулам (2,3):

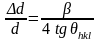, (2)

. (3)