Приклад 12. Оцінка рівня сезонності часового ряду
Знайти
оцінки рівня сезонності часового ряду,
представленого в табл. 12.6, через індекси
сезонності, проводячи обчислення
за формулою (12.44).
Розв’язання
Скористаємося
табл. 12.9, 12.12, в яких приведені значення
тренду
і сезонної компоненти
.
В результаті отримаємо табл. 12.13, що
складається з коефіцієнтів
.
У
передостанньому рядку табл. 12.13 приведені
суми
по стовпчиках, в останньому рядку –
індекси сезонності
.
Таблиця 12.13. Коефіцієнти
Рік |
Місяць |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
2 |
0,55 |
0,48 |
1,88 |
1,02 |
1,23 |
1,26 |
1,28 |
1,29 |
1Д7 |
1,11 |
0,89 |
0,81 |
3 |
0,68 |
0,62 |
0,91 |
1,02 |
1,17 |
1,19 |
1,21 |
1,23 |
1,13 |
1,09 |
0,19 |
0,85 |
4 |
0,68 |
0,63 |
0,91 |
1,02 |
1,16 |
1,19 |
1,20 |
1,22 |
1,12 |
1,08 |
0,92 |
0,85 |
5 |
0,73 |
0,68 |
0,92 |
1,01 |
1,14 |
1,16 |
1,17 |
1,18 |
1,10 |
1,07 |
0,94 |
0,89 |
6 |
0,71 |
0,66 |
0,92 |
1,01 |
1Д5 |
1Д7 |
1,18 |
1,20 |
1,12 |
1,08 |
0,93 |
0,87 |
7 |
0,72 |
0,67 |
0,92 |
1,01 |
1,14 |
1,16 |
1,18 |
1,19 |
1,10 |
1,07 |
0,93 |
0,88 |
8 |
0,74 |
0,70 |
0,93 |
1,01 |
1,14 |
1,15 |
1,16 |
1,18 |
1,10 |
1,06 |
0,94 |
0,89 |
9 |
0,79 |
0,75 |
0,94 |
1,01 |
1,11 |
1,12 |
1,14 |
1,05 |
1,08 |
1,06 |
0,95 |
0,90 |
10 |
0,77 |
0,73 |
0,94 |
1,01 |
1,12 |
1,14 |
1,15 |
1,16 |
1,09 |
1,06 |
0,94 |
0,90 |
11 |
0,80 |
0,77 |
0,95 |
1,01 |
1,10 |
1,12 |
1,13 |
1,13 |
1,08 |
1,05 |
0,95 |
0,91 |
12 |
0,84 |
0,82 |
0,96 |
1,01 |
1,08 |
1,09 |
1Д0 |
1,11 |
1,06 |
1,04 |
0,96 |
0,94 |
|
8,01 |
7,51 |
10,18 |
11,14 |
12,54 |
12,75 |
12,90 |
13,04 |
12,15 |
11,77 |
10,26 |
9,69 |
|
72,80 |
68,30 |
92,50 |
101,3 |
114,0 |
115,9 |
117,3 |
118,5 |
110,5 |
107,0 |
93,3 |
88,1 |
,
%
В 1-му, 2-му, 3-му і 11-му, 12-му місяцях рівень часового ряду менше значень тренду, а в 4-му - 10-м цей рівень більше значень тренду.
Таким
чином, в економічному явищі (обсяг
перевезень морським транспортом) явно
присутня сезонна складова з піком в
літні місяці. Кількісну характеристику
цієї сезонності дає сезонна хвиля у
вигляді сукупності індексів сезонності,
представлених в останньому рядку
табл.12.13. Якщо відмітити отримані значення
(%) на координатній площині, то можна
отримати графічне зображення досліджуваної
сезонної хвилі (рис. 12.3), яка досить
адекватно відтворює фактичну зміну
процесу впродовж року, відображеного
на рис. 12.2.
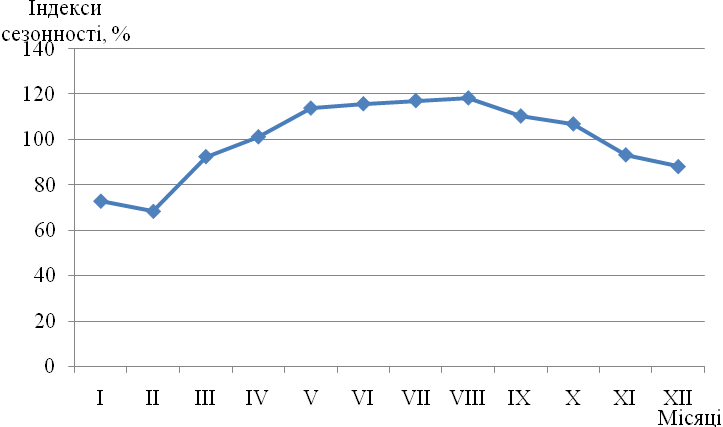
Рис. 12.3. Сезонна хвиля обсягів перевезень вантажів морським транспортом