12.5. Ітераційні методи фільтрації

При виділенні (фільтрації) компонент часового ряду за допомогою тих або інших методів неминуче встає питання про «чистоту» фільтрації, тобто питання про міру близькості оцінок і їх істинним значенням , . Слід зазначити, що досі жоден з відомих методів не забезпечує необхідної міри чистоти фільтрації для часових рядів різної структури.

Ітераційні методи фільтрації складових часового ряду з’явилися свого часу як результат визнання неможливості виділення компонент ряду прямими методами. Основна ідея ітераційних процедур полягає у багатократному застосуванні плинної середньої:

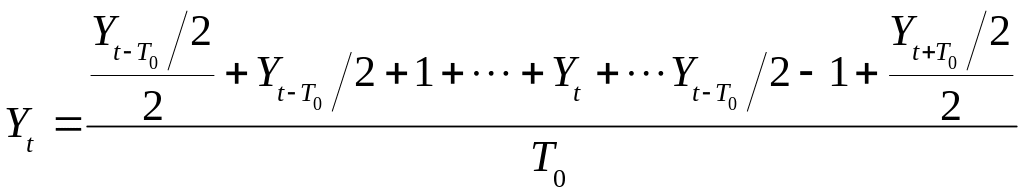(12.19)

і одночасній оцінці сезонної компоненти в кожному циклі. При цьому перехід від одного кроку ітераційної процедури до іншого може супроводжуватися зміною параметрів плинної середньої. Якщо формулу для плинної середньої записати у вигляді:

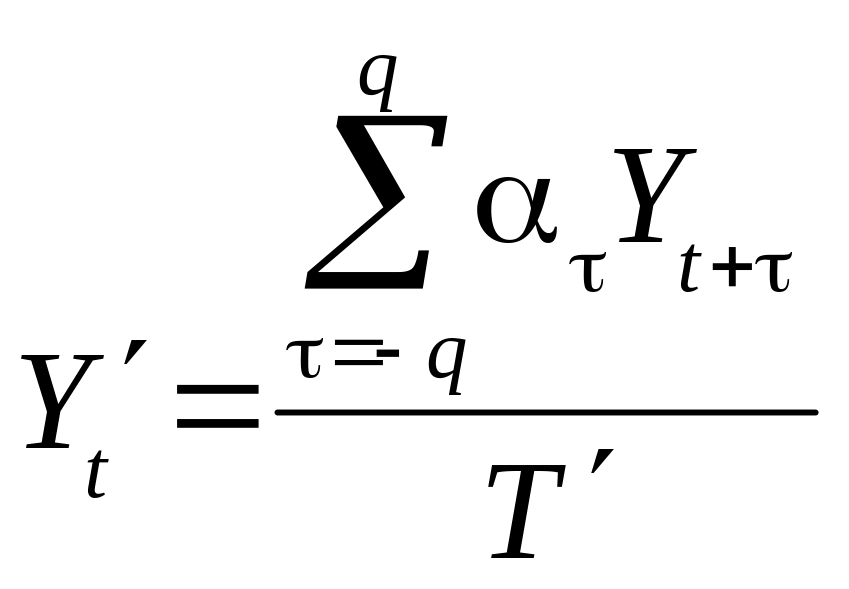(12.20)

то при переході від однієї ітерації до іншої може відбуватися зміна довжини відрізку плинності і закону зміни вагових коефіцієнтів . У деяких ітераційних методах, крім того, використовується регресія (як правило, лінійна) початкового ряду на перетворений в першому кроці ряд .

Ітераційні методи відрізняє простота і задовільна «чистота» фільтрації компонент ряду. Проте усім їм властивий і істотний недолік. Застосування плинної середньої (12.19) і (12.20) призводить до втрати частини інформації на кінцях часового ряду.

Розглянемо два ітераційні методи: Четверикова і Шіскіна-Ейзенпресса.

Метод Четверикова.1. Емпіричний ряд вирівнюється плинною середньою (12.19) з періодом , тобто береться членів початкового ряду, з яких перший і останній береться з половинною вагою: . членів ряду, які випадають з обох його кінців, або відновлюються екстраполяцією ряду, що вирівнюється, або не враховуються при подальшому аналізі.

Попередня оцінка тренду – і відхилення емпіричного ряду від того, що вирівнюється – , чи ,

2. Для кожного року обчислюється – середньоквадратичне відхилення, на яке діляться окремі місячні (квартальні) відхилення відповідного року:

(12.21)

де

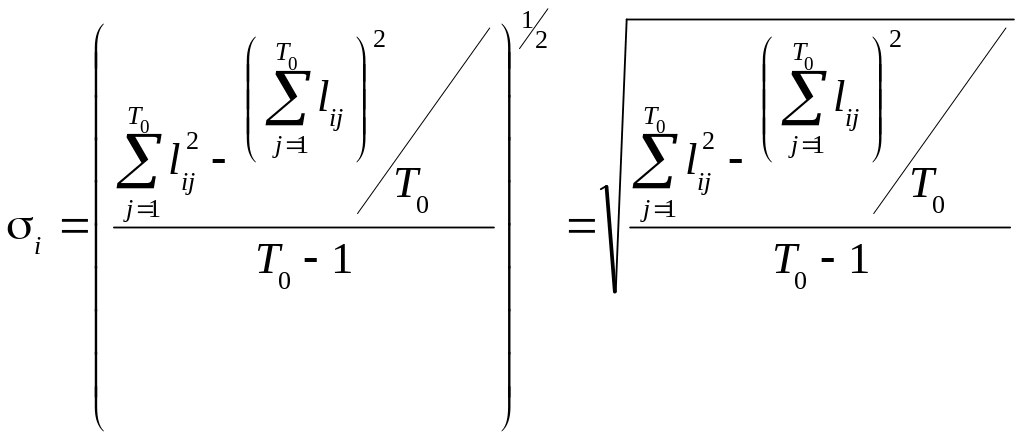(12.22)

3. З «нормованих» таким чином відхилень обчислюють попередню середню сезонну хвилю:

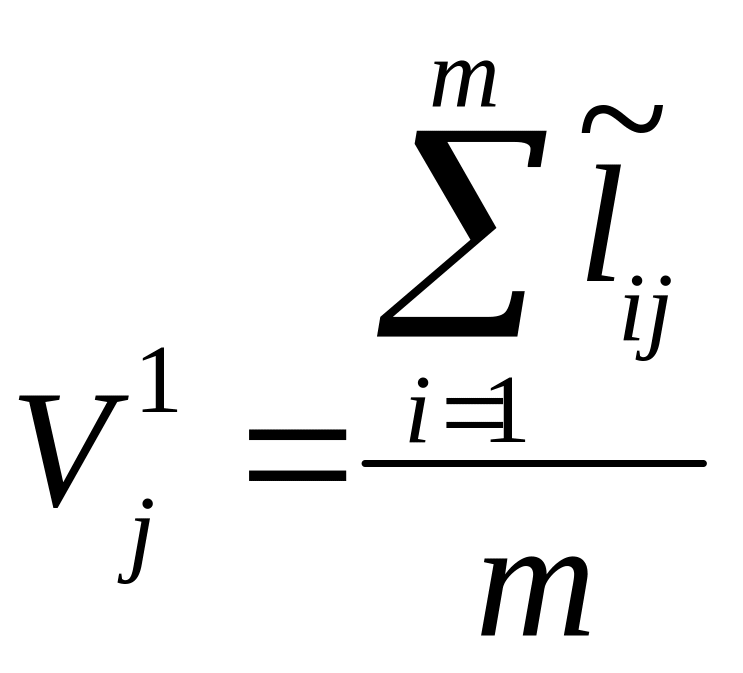(12.23)

4. Середню попередню сезонну хвилю домножають на середньоквадратичне відхилення кожного року і віднімають з емпіричного ряду:

(12.24)

5. Отриманий ряд, позбавлений попередньої сезонної хвилі, знову згладжується плинною середньою (для місячних даних по п’яти або семи точкам, залежно від інтенсивності незначних кон’юнктурних коливань і тривалості більш значних). В результаті виходить нова оцінка тренду .

6. Відхилення емпіричного ряду від ряду , отриманого в п. 5 даної методики.

(12.25)

знову піддаються аналогічній обробці по пп. 2 і 3 для виявлення остаточної середньої сезонної хвилі.

7. Виключення остаточної сезонної хвилі отримують після множення середньої сезонної хвилі на – коефіцієнт напруженості сезонної хвилі:

, (12.26)

де – значення ряду, що вирівнюються, – випадкова компонента:

(12.27)

Метод Шіскіна-Ейзенпресса

У методиці Шіскіна-Ейзенпресса, окрім плинної середньої (12.19), на другому і подальших етапах ітераційної процедури застосовують складніші п’ятнадцяти- і двадцатиодноточечні плинні Спенсера. Вони мають відповідно вигляд:

(12.28)

(12.29)

чи в цифровому записі Кендалла:

(12.30)

(12.31)

В (12.30) і (12.13) символи означають вирівнювання ряду плинною середньою. Так, наприклад, якщо , то

(12.32)

Символ означає подвійне послідовне вирівнювання ряду однією і тією ж плинною середньою, тобто якщо , то спочатку отримуємо оцінки , що вирівнюються, по (12.32), потім до них застосуємо ту ж плинну середню (12.32):

(12.33)

Якщо розглядається двадцатиодноточкова плинна середня (12.28), то потім потрібно було б застосувати ще одне вирівнювання по семи точках:

(12.34)

І на завершення:

(12.35)

В результаті отримують вираз (12.28).

Плинна середня з симетрично-рівними вагами виду (12.19) дозволяє виділити лише лінійний тренд. Якщо ж тренд насправді нелінійний, то згладжування часового ряду, що містить нелінійний тренд, дає спотворені його значення. Плинна середня Спенсера дозволяє отримувати точні оцінки тренду, вираженого поліномами до третього ступеня включно.

Розглянемо тепер власне метод Шискина-Эйзенпресса.

1. Початковий ряд вирівнюється плинною середньою (12.19). Це дозволяє не спотворювати сезонну компоненту . Використання плинної середньої з іншим періодом привело б до зміни як амплітуди, так і форми сезонної хвилі.

2. Розраховують залишкові значення:

чи

Обчислюють середні значення залишкового ряду в цілому по ряду і по місяцях (кварталам) :

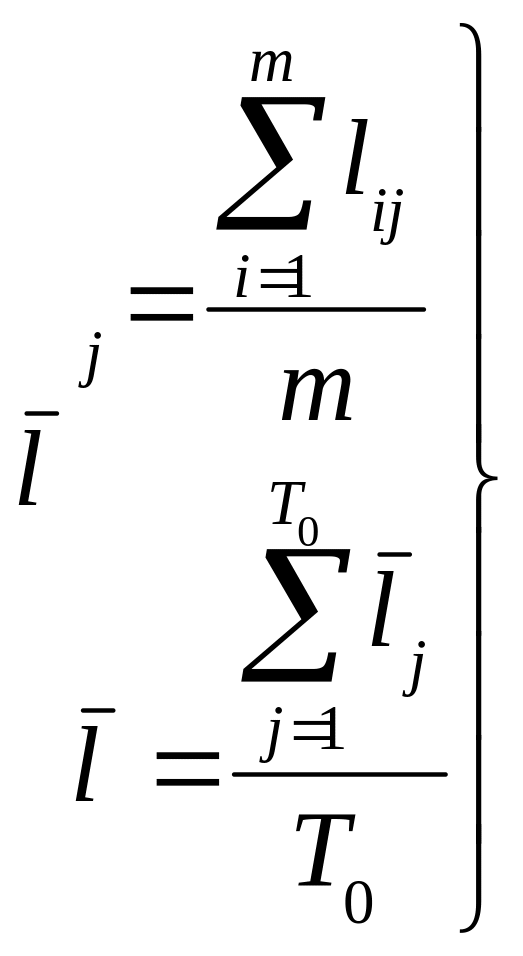(12.36)

3. Знаходять попередню оцінку середньої сезонної хвилі:

(12.37)

і будують новий ряд, відносно вільний від сезонної компоненти:

(12.38)

4. До ряду застосовують згладжування плинною середньою Спенсера:

(12.39)

Знаходять поліпшену оцінку сезонної компоненти:

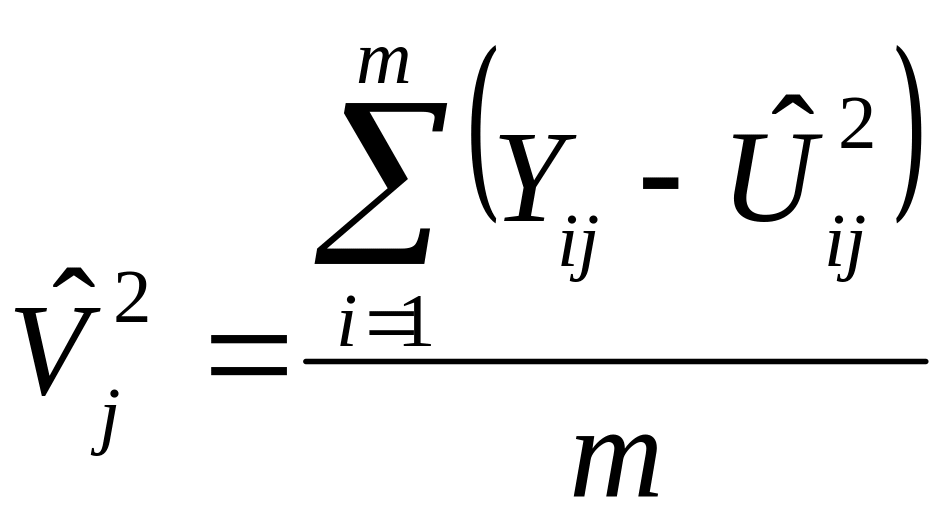(12.40)