12.3. Згладжування тимчасових рядів економічних показників

Дуже часто рівні економічних рядів динаміки коливаються, при цьому тенденція розвитку економічного явища в часі прихована випадковими відхиленнями рівнів в ту або іншу сторону. З метою виявити тенденцію розвитку досліджуваного процесу, у тому числі для подальшого застосування методів прогнозування на основі трендових моделей, виконують згладжування (вирівнювання) часових рядів.

Методи згладжування тимчасових рядів діляться на дві основні групи:

– аналітичне вирівнювання з використанням кривої, проведеної між конкретними рівнями ряду так, щоб вона відображала тенденцію, властиву ряду, і одночасно звільняла його від незначних коливань;

– механічне вирівнювання окремих рівнів часового ряду з використанням фактичних значень сусідніх рівнів.

Суть методів механічного згладжування полягає в наступному. Беруть декілька перших рівнів часового ряду, що утворюють інтервал згладжування. Для них підбирається поліном, спепінь якого має бути менше числа рівнів, що входять в інтервал згладжування; за допомогою полінома визначаються нові значення рівнів, вирівняні в середині інтервалу згладжування. Далі інтервал згладжування зміщується на один рівень ряду вправо, обчислюється наступне згладжене значення і т. д.

Найпростішим методом механічного згладжування є метод простої плинної середньою. Спочатку для часового ряду визначається інтервал згладжування ( < ). Якщо необхідно згладити незначні безладні коливання, то інтервал згладжування беруть по можливості великим; інтервал згладжування зменшують, якщо потрібно зберегти незначні коливання. За інших рівних умов, інтервал згладжування рекомендується брати непарним. Для перших рівнів часового ряду обчислюється їх середня арифметична; це буде згладжене значення рівня ряду, що знаходиться в середині інтервалу згладжування. Потім інтервал згладжування зміщується на один рівень вправо, повторюється обчислення середньої арифметичної і т.д. Для обчислення згладжених рівнів ряду використовується формула:

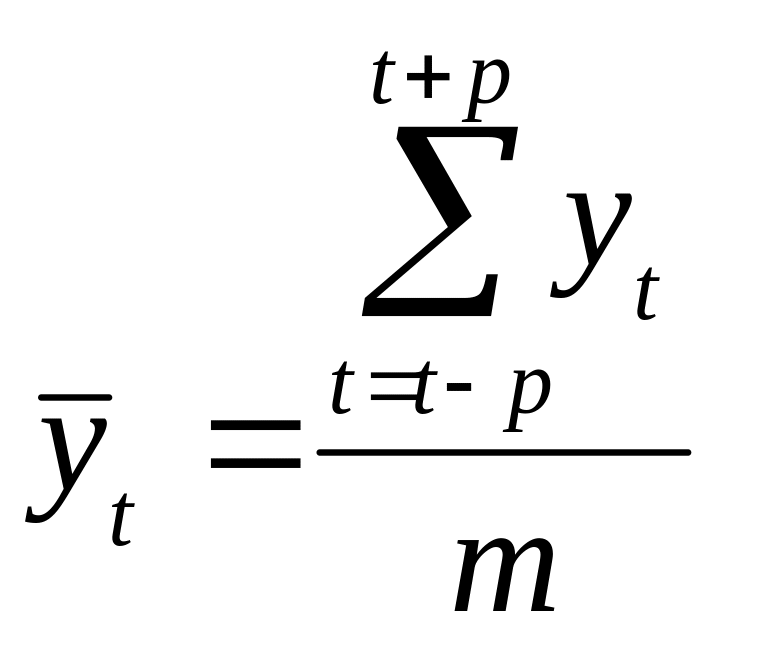, > , (12.9)

де (при непарному ); для парних формула ускладнюється.

В результаті такої процедури виходять згладжених значень рівнів ряду; при цьому перші і останні рівнів ряду втрачаються (не згладжуються).

Інший недолік методу в тому, що він застосовний лише для рядів, що мають лінійну тенденцію.

Метод зваженої плинної середньої відрізняється від попереднього методу згладжування тим, що рівні, що входять в інтервал згладжування, підсумовуються з різними вагами. Це пов’язано з тим, що апроксимація ряду в межах інтервалу згладжування здійснюється з використанням полінома не першого степеня, як у попередньому випадку, а починаючи з другого. Використовується формула середньої арифметичної зваженої:

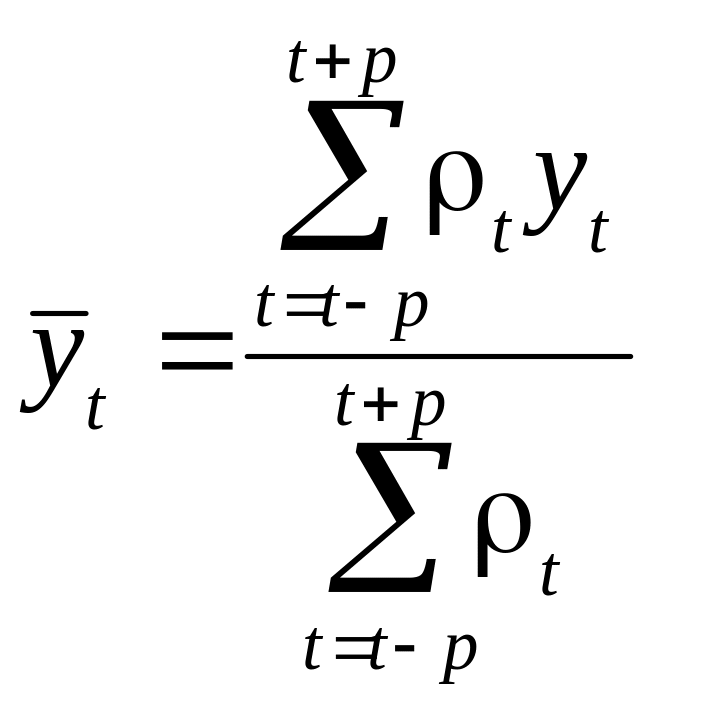, (12.10)

причому ваги визначаються за допомогою методу найменших квадратів. Ці ваги розраховані для різних степенів апроксимуючого полінома і різних інтервалів згладжування. Так, для поліномів другого і третього порядків числова послідовність ваг при інтервалі згладжування має вигляд: {- 3; 12; 17; 12; - 3}, а при має вигляд: {- 2; 3; 6; 7; 6; 3; - 2}. Для поліномів четвертого і п’ятого степенів і при інтервалі згладжування послідовність ваг виглядає таким чином: {5; - 30; 75; 131; 75; - 30; 5}.

До цієї ж групи методів вирівнювання часових рядів відноситься метод експоненційного згладжування. Його особливість полягає в тому, що в процедурі знаходження згладженого рівня використовуються значення тільки попередніх рівнів ряду, узяті з певною вагою, причому вага спостереження зменшується в міру віддалення його від моменту часу, для якого визначається згладжене значення рівня ряду. Якщо для початкового часового ряду відповідні згладжені значення рівнів позначити через , , то експоненційне згладжування здійснюється за формулою:

, (12.11)

де – параметр згладжування (0< <1); величина називається коефіцієнтом дисконтування.

Використовуючи приведене вище рекурентне співвідношення для усіх рівнів ряду, починаючи з першого і закінчуючи моментом часу , можна отримати, що експоненційна середня, тобто згладжене цим методом значення рівня ряду, є зваженою середньою усіх попередніх рівнів:

; (12.12)

тут – величина, що характеризує початкові умови.

В практичних завданнях обробки економічних тимчасових рядів рекомендується (необґрунтовано) вибирати величину параметра згладжування в інтервалі від 0,1 до 0,3. Інших точних рекомендацій для вибору оптимальної величини параметра не має. В окремих випадках Р. Браун пропонує визначати величину виходячи з довжини згладжуваного ряду:

(12.13)

Що стосується початкового параметра , то в конкретних завданнях його беруть або рівним значенню першого рівня ряду , або рівним середній арифметичній декількох перших членів ряду, наприклад, членів , , :

(12.14)

Вказаний вище порядок вибору величини забезпечує хороше узгодження згладженого і початкового рядів для перших рівнів. Якщо ближче до правого кінця часового ряду згладжені цим методом значення при вибраному параметрі починають значно відрізнятися від відповідних значень початкового ряду, необхідно перейти на інший параметр згладжування. Відмітимо, що при цьому методі згладжування не втрачаються ні початкові, ні кінцеві рівні згладжуваного часового ряду.