12.2. Попередній аналіз і згладжування часових рядів економічних показників

Попередній аналіз тимчасових рядів економічних показників полягає в основному у виявленні і усуненні аномальних значень рівнів ряду, а також у визначенні наявності тренду в початковому часовому ряду.

Під аномальним рівнем розуміють окреме значення рівня часового ряду, яке не відповідає потенційним можливостям досліджуваної економічної системи і яке, залишаючись в якості рівня ряду, істотно впливає на значення основних характеристик часового ряду, у тому числі на відповідну трендову модель. Причинами аномальних спостережень можуть бути помилки технічного порядку, або помилки першого роду: помилки при агрегації і дезагрегуванні показників, при передачі інформації і ін. технічні причини. Помилки першого роду підлягають виявленню і усуненню. Крім того, аномальні рівні в тимчасових рядах можуть виникати через вплив чинників, що мають об’єктивний характер, але що проявляються епізодично, дуже рідко – помилки другого роду; вони усуненню не підлягають.

Для виявлення аномальних рівнів тимчасових рядів використовуються методи, розраховані для статистичних сукупностей.

Метод Ірвіна – припускає використання наступної формули:

, (12.1)

де – середньоквадратичне відхилення, що розраховується у свою чергу з використанням формул:

(12.2)

Розрахункові значення , і т. д. порівнюються з табличними значеннями критерію Ірвіна і якщо виявляються більше за табличні, то відповідне значення рівня ряду вважається аномальним. Значення критерію Ірвіна для рівня значимості , тобто з 5%-вою помилкою, приведені в табл. 12.4.

Таблиця 12.4. Критичні значення критерію Ірвіна для рівня значимості

	2	3	10	20	30	50	100
	2,8	2,3	1,5	1,3	1,2	1,1	1,0

Після виявлення аномальних рівнів ряду визначають причини їх виникнення. Якщо точно встановлено, що вони викликані помилками першого роду, то вони усуваються або заміною аномальних рівнів простою середньою арифметичною двох сусідніх рівнів ряду, або заміною аномальних рівнів відповідними значеннями по кривій, що апроксимує цей часовий ряд. Порядок знаходження такої кривої, тобто трендової моделі, розглядається нижче.

Для визначення наявності тренду в початковому часовому ряду застосовується декілька методів.

Метод перевірки різниць середніх рівнів. Реалізація цього методу складається з чотирьох етапів.

На першому етапі початковий часовий ряд розбивається на дві приблизно рівні по числу рівнів частини: в першій частині перших рівнів початкового ряду, в другій – інших рівнів .

На другому етапі для кожної з цих частин обчислюються середні значення і дисперсії:

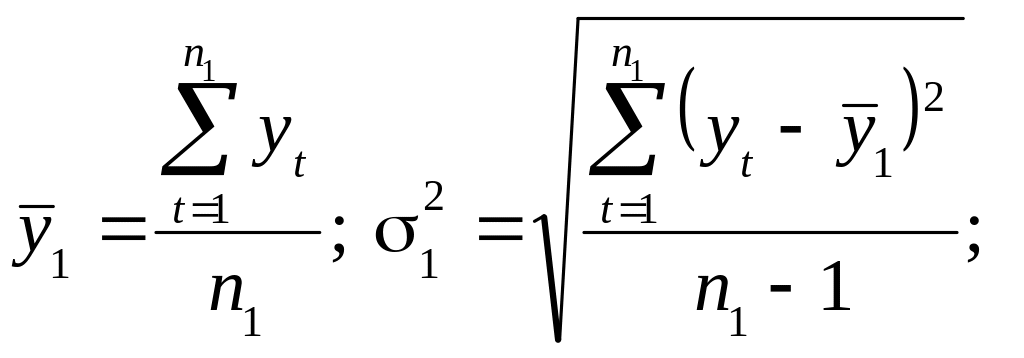
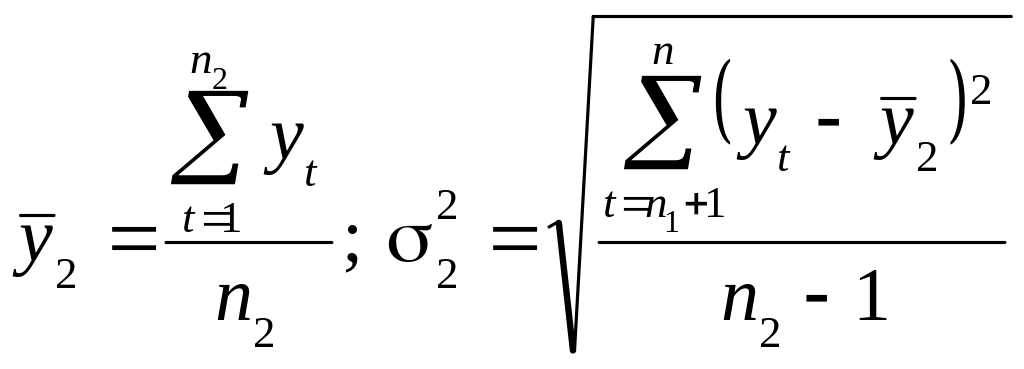(12.3)

Третій етап полягає в перевірці рівності (однорідності) дисперсій обох частин ряду за допомогою -критерію Фішера, яка заснована на порівнянні розрахункового значення цього критерію:

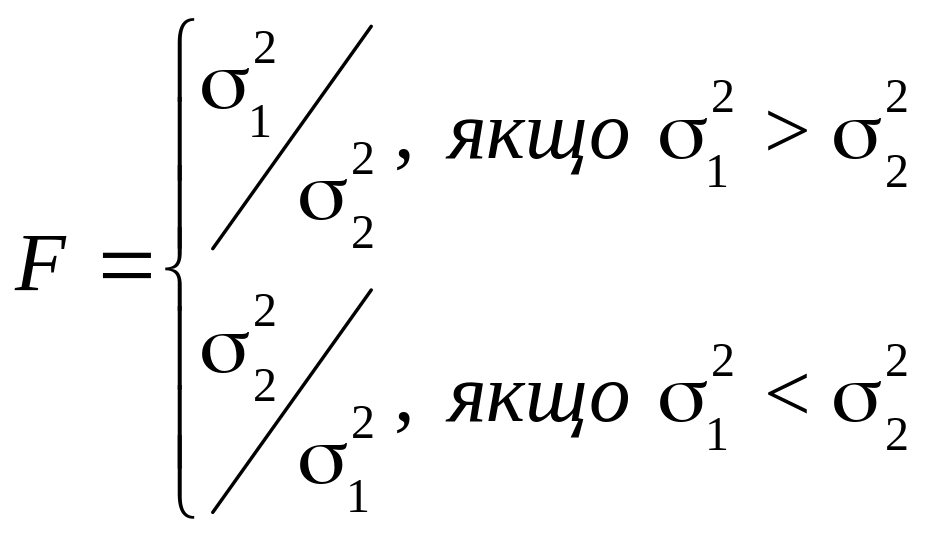(12.4)

з табличним (критичним) значенням із заданим рівнем значимості (рівнем помилки) . В якості найчастіше беруть значення 0,1 (10%-на помилка), 0,05 (5%-на помилка), 0,01 (1%-на помилка). Величина називається довірчою вірогідністю.

Якщо розрахункове значення менше за табличне , то гіпотеза про рівність дисперсій приймається і переходять до четвертого етапу. Якщо більше або рівно табличного , то гіпотеза про рівність дисперсій відхиляється і робиться висновок, що цей метод для визначення наявності тренду відповіді не дає.

На четвертому етапі перевіряється гіпотеза про відсутність тренду з використанням -критерію Стьюдента. Для цього визначається розрахункове значення критерію Стьюдента за формулою:

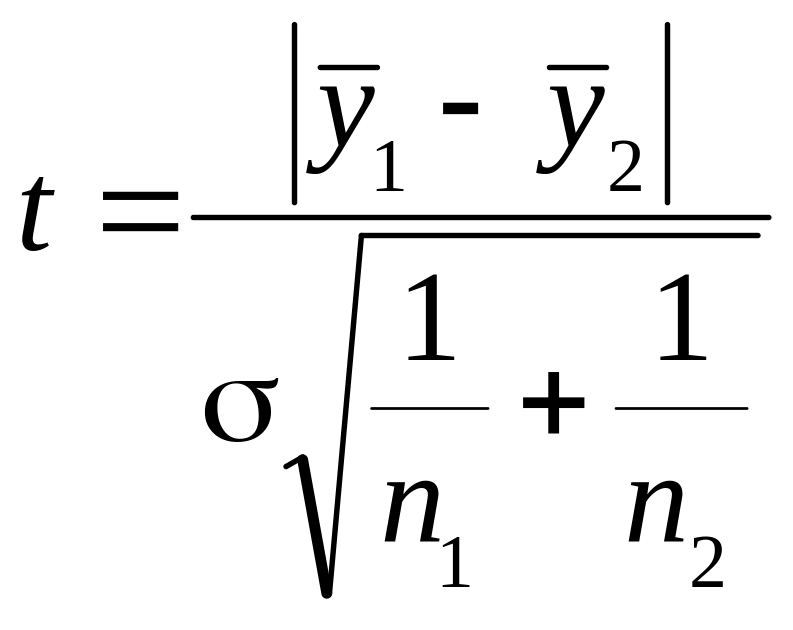, (12.5)

де – середньоквадратичне відхилення різниці середніх:

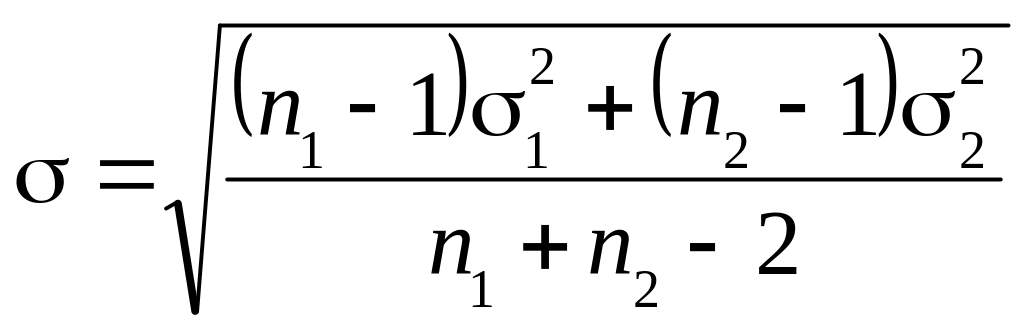(12.6)

Якщо розрахункове значення менше табличного значення статистики Стьюдента із заданим рівнем значимості , гіпотеза приймається, тобто тренду немає, інакше тренд є. Помітимо, що в даному випадку табличне значення береться для числа ступенів свободи, рівного , при цьому цей метод застосовний тільки для рядів з монотонною тенденцією.

Метод Фостера-Стьюарта. Цей метод має більше можливостей і дає надійніші результати в порівнянні з попереднім. Окрім тренду самого ряду (як то кажуть, тренду в середньому), він дозволяє встановити наявність тренду дисперсії часового ряду: якщо тренду дисперсії немає, то розкид рівнів ряду постійний; якщо дисперсія збільшується, то ряд «розгойдується» і т. д.

Реалізація методу також містить чотири етапи.

На першому етапі порівнюють кожний рівень початкового часового ряду, починаючи з другого рівня, з усіма попередніми, при цьому визначають дві числові послідовності:

На другому етапі обчислюють величини і :

; (12.6)

Величина , що характеризує зміну часового ряду, набуває значень від 0 (усі рівні ряду рівні між собою) до (ряд монотонний). Величина характеризує зміну дисперсії рівнів часового ряду і змінюється від (ряд монотонно спадає) до (ряд монотонно зростає).

Третій етап полягає в перевірці гіпотез:

– чи можна вважати випадковим відхилення величини від величини – математичного очікування величини для ряду, в якому рівні розташовані випадковим чином,

– відхилення величини від нуля.

Ця перевірка проводиться з використанням розрахункових значень -критерия Стьюдента для середньої і для дисперсії:

; (12.7)

, (12.8)

де – математичне очікування величини , визначеною для ряду, в якому рівні розташовані випадковим чином; - середньоквадратичне відхилення для величини ; - середньоквадратичне відхилення для величини d.

Для зручності є табульовані значення величин , і ; фрагменти цих значень представлені в табл. 12.5.

Таблиця 12.5. Значення , і

	10	20	30	40
	3,858	5,195	5,990	6,557
	1,288	1,677	1,882	2,019
	1,964	2,279	2,447	2,561

На четвертому етапі розрахункові значення і порівнюються з табличним значенням -критерія Стьюдента із заданим рівнем значимості . Якщо розрахункове значення менше за табличне, то гіпотеза про відсутність відповідного тренду приймається; інакше тренд є. Наприклад, якщо більше табличного значення , a менше , то для цього часового ряду є тренд в середньому, а тренду дисперсії рівнів ряду немає.

Приклад визначення наявності тренду методом Фостера-Стьюарта наведений в п. 12.4.