Приклад 10. Виробнича функція Кобба-Дугласа

Виробнича функція (регресія Кобба–Дугласа) має вигляд:

,

де – обсяг виробництва, млн. грн., – працезатрати, тис. людино-дн., – основні засоби, тис. грн.

На основі статистичних даних (табл10.1.) знайти оцінки параметрів виробничої регресії.

З надійністю встановити адекватність прийнятої математичної моделі статистичним даним. Якщо модель адекватна статистичним даним, то знайти частинні коефіцієнти еластичності, значення прогнозу та його надійного інтервалу.

Побудувати ізокванту для .

Таблиця 10.1. Вихідні дані задачі

	33,3	38,5	40,4	45,8	46,2	50,0	52,1	56,7	57,9	60,5	63,0	65,1	66,6	67,2
	44,4	47,3	48,2	49,8	52,2	54,3	54,4	58,7	61,5	63,8	64,2	65,0	65,4	66,0
	70,1	78,6	81,7	88,7	90,8	96,4	99,7	106,1	109,2	112,8	117,1	119,1	123,2	124,0

Розв’язання

Дана модель – нелінійна двохфакторна регресія. Для оцінки її параметрів приведемо моджель до лінійного виду шляхом логарифмування лівої та правої частин рівняння та заміни змінних: . Отримуємо приведену лінійну регресію: , де .

Запишемо приведену лінійну модель в матричному вигляді:

,

де – вектор-стовпчик результатів, – матриця факторів, – вектор-стовпчик оцінок параметрів, тобто:

;

; ;

Якщо , то .

Отже, , тоді . Виробнича функція має вигляд:

Перевіримо адекватність прийнятої математичної моделі статистичним даним з допомогою критерію Фішера.

Таблиця 10.2. Розрахункові дані задачі

4,25	4,25	0,000000	70,10	70,06	972,86	970,32
4,36	4,36	0,000006	78,60	78,41	521,51	513,02
4,40	4,40	0,000017	81,70	81,37	395,32	382,20
4,49	4,49	0,000047	88,70	89,31	142,60	157,50
4,51	4,51	0,000002	90,80	90,67	111,90	109,20
4,57	4,57	0,000001	96,40	96,50	22,53	23,52
4,60	4,60	0,000014	99,70	99,32	3,71	2,40
4,66	4,67	0,000053	106,10	106,88	31,67	23,52
4,69	4,70	0,000004	109,20	109,42	66,79	63,20
4,73	4,73	0,000051	112,80	113,61	152,65	133,40
4,76	4,76	0,000001	117,10	116,97	247,24	251,22
4,78	4,79	0,000050	119,10	119,95	349,52	318,62
4,81	4,80	0,000096	123,20	122,00	430,39	481,80
4,82	4,81	0,000069	124,00	122,97	471,88	517,56

Обчислимо значення коефіцієнта детермінації: . Отже, варіація обсягу виробництва на залежить від варіації працезатрат та обсягу основних засобів. Тоді, . Оскільки для і ступенів свободи та рівня значимості . , тобто, з надійністю 0,95 можна вважати, що прийнята математична модель адекватна експериментальним даним і її можна застосовувати для аналізу господарської діяльності підприємства.

Параметри , є частинними коефіцієнтами еластичності, тобто збільшення фактора (працевитрати ) на 1% при незмінному факторі (основні засоби) викликає зміну обсягу випуску продукції на 0,69%, а збільшення фактора (основні засоби) на 1% при незмінному факторі (працевитрати) викликає зміну обсягу випуску продукції на 0, 19 %.

Сумарний коефіцієнт еластичності , тобто при збільшенні обсягу основних засобів та працевитрат в разів, обсяг випуску продукції збільшиться в разів, з розширенням масштабів виробництва середні витрати ресурсів в розрахунку на одиницю продукції будуть збільшуватися, тому це не доцільно.

Для обчислення значення прогнозу та його надійного інтервалу прогнозні значення змінних та : тис. люд.-днів, тис. грн.

млн. грн.

Знайдемо довірчий інтервал прогнозного значення :

;

Якщо кількість ступенів свободи і рівень значимості , то . Для лінійної моделі .

Тоді:

або

Отже, з надійністю 0,95 при рівні працезатрат тис. люд.-днів та вартості основних засобів тис. грн. прогнозується обсяг виробництва не менше 129,35 млн. грн., але не більше 160,93 млн. грн.

Для наочного уявлення взаємозамінюваності факторів побудуємо ізокванту.

Нехай . Використовуючи залежність між , та , виразимо через та :

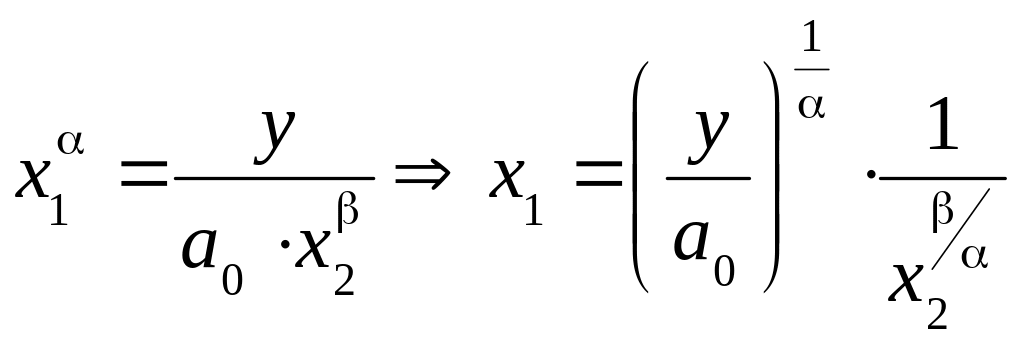
Позначимо: 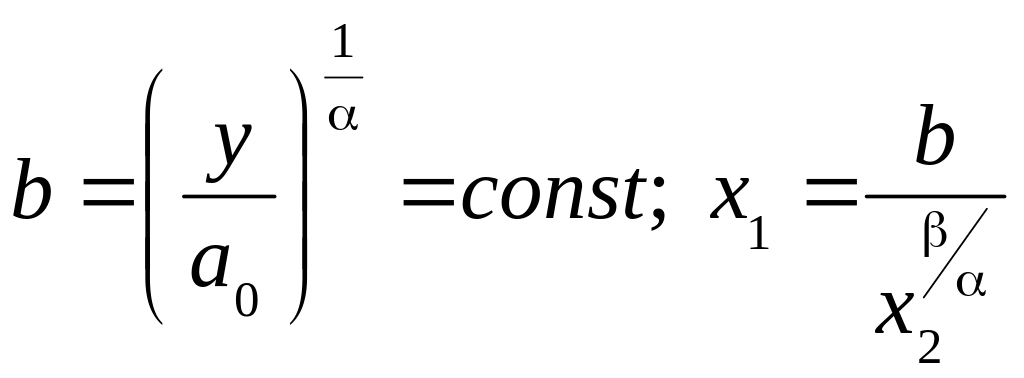. Знайдемо значення параметра b:

Обчислимо для значення в залежності від :

Таблиця 10.3. Розрахункові дані задачі

	44,4	47,3	48,2	49,8	52,2	54,3	54,4	58,7	61,5	63,8	64,2	65,0	65,4	66,0
	36,13	34,69	34,22	33,04	32,96	32,24	31,87	31,12	30,94	30,56	30,21	29,94	29,74	29,67

Ізокванта в декартовій системі координат матиме вигляд (рис. 10.2.):

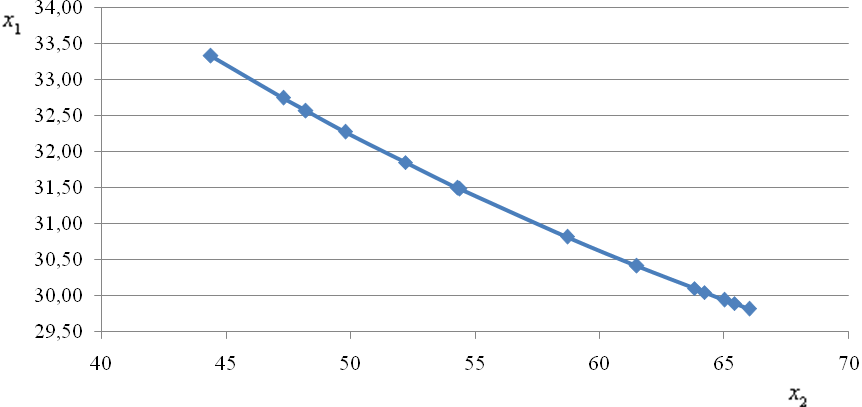
Рис. 10.2. Ізокванта

Даний графік дозволяє визначити комбінації факторів, яким відповідає обсяг виробництва млн. грн.