11.2. Різновиди виробничих функцій

У прогнозних розрахунках використовується понад 100 модифікацій виробничих функцій, які відрізняються одна від іншої аналітичним видом, характером і специфікою параметрів, що враховуються. На наш погляд, найбільший інтерес представляють моделі, які можуть бути безпосередньо використані для комплексного економічного аналізу і прогнозування. Тому далі розглядаються виробничі функції, що мають реальний економічний зміст і реалізуються на практиці при сформованій системі інформаційного і математичного забезпечення.

Найбільш розповсюдженими й в той же час найпростішими видами виробничих функцій, які широко застосовуються в регіональному і галузевому прогнозуванні, є наступні моделі технологічних взаємозв’язків:

Лінійна:

(11.2)

Кобба – Дугласа:

(11.3)

Функція постійної еластичності заміни:

(11.4)

де – обсяг виробництва продукції; – обсяг виробничих фондів; – чисельність зайнятих; - параметри виробничих функцій, конкретні числові значення яких визначаються методами математичної статистики.

У лінійній моделі передбачається лінійна залежність випуску від витрат. До переваг моделі відноситься відносна простота оцінки шуканих параметрів, а також задовільна апроксимація базисних обсягів виробництва при чітко вираженій тенденції їх зміни. При використанні лінійної виробничої функції передбачається, що трудові ресурси й основні виробничі фонди як фактори виробництва цілком замінювані. Приріст продукту, гранична продуктивність і гранична норма заміщення постійні, не залежать від обсягів виробничих ресурсів і відповідно рівні

(11.5)

Еластичність заміщення ресурсів у моделі I нескінченно велика ( ), а еластичність виробництва дорівнює одиниці.

З математичних властивостей моделі (11.2) випливає, що лінійна виробнича функція передбачає постійну віддачу ресурсів. При збільшенні основних виробничих фондів на 1% масштаби випуску збільшуються на %, а при збільшенні чисельності зайнятих на 1% – на %. При цьому співвідношення (пропорції) між ресурсами не мають значення.

Таким чином, лінійна виробнича функція спрощує реальні процеси в сфері виробництва, тому що абстрагується від ряду істотних умов і факторів. Однак, коли задачею дослідження є не глибокий економічний аналіз, а комплексне прогнозування ресурсів і результатів виробничої діяльності, особливо на основі системи економетричних рівнянь, використання залежності (11.1) доцільно і знаходить широке застосування.

11.3. Виробнича функція Кобба-Дугласа

Більш адекватно відбиває реальні процеси виробнича функція Кобба - Дугласа II. Аналітичний вигляд цієї функції також допускає можливість моделювання взаємозамінності ресурсів, однак на відміну від лінійної функції випуск продукції дорівнює нулеві, якщо або ; еластичність заміщення менша і цінність ресурсу зменшується, коли питома вага його в загальних витратах росте.

З виразу (11.3) очевидно, що гранична продуктивність і гранична норма заміщення рівні

(11.6)

(11.7)

З (11.6) випливає, що при фіксованому випуску продукції у функції Кобба-Дугласа гранична продуктивність знижується з ростом величини використовуваних фондів і трудових ресурсів. Норма заміщення (11.7) зростає зі збільшенням питомих витрат одного з ресурсів, тобто, для заміщення одиниці одного виду ресурсів потрібна зростаюча кількість додаткових витрат іншого виду ресурсів.

Функція Кобба-Дугласа допускає ряд методологічних спрощень. По-перше, обсяг випуску продукції з ростом фондоозброєності може необмежено зростати, тобто 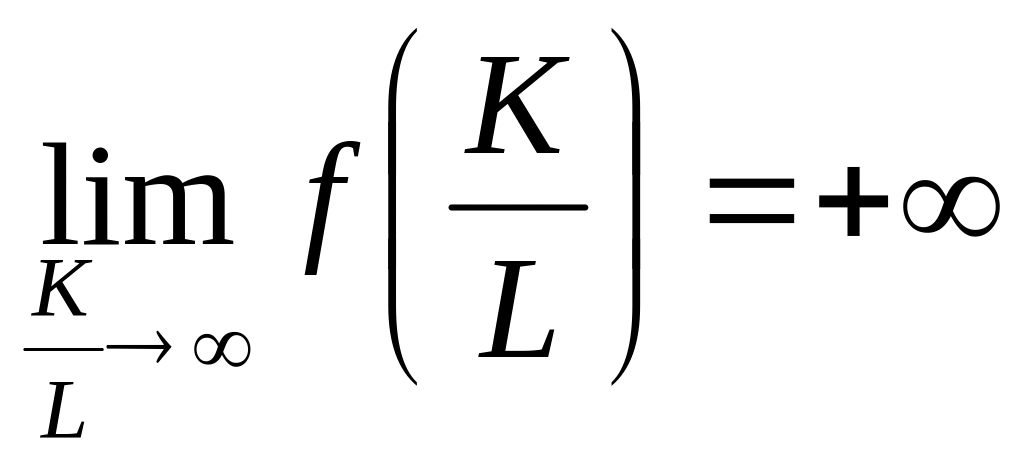. По – друге, будь – яка кількість продукції може бути виготовлена при як завгодно малій величині основних фондів та при достатньо великій кількості трудових ресурсів, та навпаки. По – третє, еластичність заміщення ресурсів при будь – якій комбінації факторів та при будь – якій капіталомісткості виробництва дорівнює одиниці. Це означає, що для збільшення норми граничної замінюваності ресурсів на 1 % необхідно збільшити співвідношення їх витрат на 1 %, що малоймовірно і не піддається економічному обґрунтуванню.

Незважаючи на ці спрощення, функції типу Кобба-Дугласа широко застосовуються в прогнозуванні і моделюванні економічних процесів.

Функція Кобба-Дугласа (СDPF) належить до найвідоміших виробничих функцій, що набули широкого застосування в економічних дослідженнях, особливо на макрорівні. Класична виробнича функція Кобба-Дугласа має вигляд:

(11.8)

де - обсяг продукції; - основний капітал; - робоча сила.

Сума параметрів або степінь однорідності класичної функції Кобба-Дугласа дорівнює одиниці. А це означає, що при збільшенні обох виробничих ресурсів на одиницю обсяг продукції також збільшиться на одиницю. Отже, ефективність ресурсів у такому разі стала.

Практичні дослідження функції Кобба-Дугласа показали, що припущення про лінійну однорідність на практиці виконується рідко. Тому була запропонована виробнича функція загальнішого вигляду.

Сума параметрів на відміну від попереднього випадку може бути як меншою, так і більшою від одиниці. Якщо > 1, те темпи росту обсягу продукції вищі за темпи росту виробничих ресурсів, а якщо < 1, то, навпаки, темпи росту продукції нижчі за темпи росту ресурсів.

Розглянемо тепер поводження функції при зміні масштабів виробництва. Припустимо, що рівень кожного виробничого ресурсові збільшився на λ, тоді величини їх відповідно дорівнюватимуть:

(11.9)

Звідси при > 1 обсяг продукції зростає більш ніж в раз; при < 1 – менш ніж в раз; при = 1 продукція збільшиться в раз. Ступінь однорідності цієї функції дорівнює . Якщо = 1, то рівень ефективності ресурсів не залежить від масштабів виробництва. Якщо <1, то, як уже стверджувалось, з розширенням масштабів виробництва середні витрати ресурсів у розрахунку на одиницю продукції збільшуються, а при > 1 - зменшуються. Причому ці властивості не залежать від числових значень і і зберігаються в кожній точці виробничої функції.

Узявши частинні похідні від виробничої функції Кобба-Дугласа, дістанемо:

(11.10)

Це означає, що граничний приріст продукції за рахунок приросту кожного ресурсу визначається як добуток коефіцієнта еластичності на середню ефективність ресурсу. Параметр а у функції Кобба-Дугласа залежить від вибраних одиниць вимірювання показників, водночас числове значення цього параметра визначається також ефективністю виробничого процесу. У цьому можна переконатись, порівнявши дві виробничі функції, які відрізняються одна від одної лише значенням параметра а.

Для фіксованих значень і тій функції, у якої більше числове значення параметра a, відповідає більше значення . Отже, і виробничий процес, який описується цією функцією, буде ефективнішим.

Наведений приклад виробничої функції показує, що ця економетрична модель дає змогу досить широко проаналізувати виробничу діяльність, визначити шляхи її вдосконалення з метою підвищення ефективності. Обґрунтованість такого аналізу повністю залежить від достовірності економетричної моделі, від того, наскільки вона адекватна реальному процесу.

Виробничі функції будуються і використовуються в основному для розв’язування задач аналізу та планування, а також задач прогнозування.

Принцип «витрати – випуск» може бути використаний для описання взаємозв’язку між обсягами ресурсів, використаних протягом року на окремому підприємстві, та річним обсягом продукції цього підприємства.

На мікроекономічному рівні в ролі виробничої системи може виступати галузь, міжгалузевий виробничий комплекс. Макроекономічні функції показують зв’язок узагальнюючого показника випуску продукції з загальними витратами ресурсів в економіці.

Для наочного уявлення про взаємозамінюваність факторів будують ізокванту – лінію рівня , множину точок, в яких обсяг виробництва сталий.

В тих виробництвах, де фактори взаємозамінні, одного й того ж результату можна досягнути різною комбінацією факторів виробництва.

Нехай кінцева мета виробництва – отримати обсяг продукції . Припустимо, що для даного виробництва оцінені параметри виробничої регресії . Необхідно знайти комбінацію факторів, при якій на підприємстві можна отримати обсяг продукції .

Використовуючи залежність між , та , виразимо через :

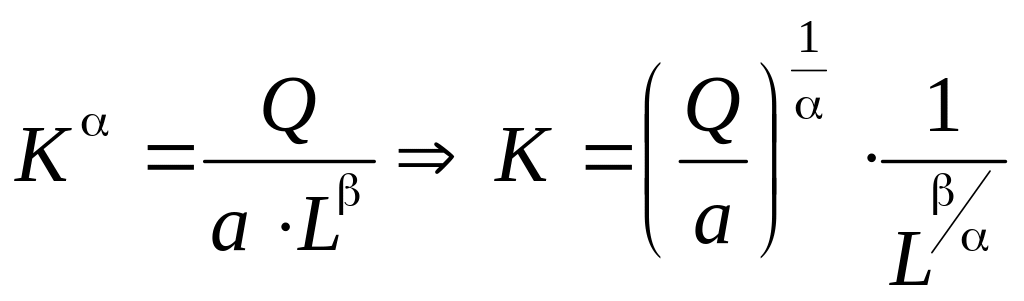(11.11)

Позначимо:

(11.12)

Для заданого ізокванта в декартові системі координат ( ; ) матиме вигляд:

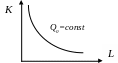
Рис. 10.1. Ізокванта

На основі аналізу властивостей перерахованих виробничих функцій можна зробити висновоки. Якщо основним завданням дослідження є прогнозування та факторний аналіз використання ресурсів економіки, то вибір аналітичного виду виробничої функції повинен визначатися найбільш адекватним відображенням досліджуваного процесу та можливістю та ефективністю оцінки параметрів. Якщо ж потрібно вирішити завдання конкретного економічного аналізу, то вони повинні визначати тип моделей, вибраних для аналізу. Такі моделі повинні мати специфічні властивості та структуру, яка відповідає завданням аналізу – включати в якості екзогенних змінних розглядувані показники, мати постійну чи змінну еластичність заміни ресурсів та ін.