10.4. Структурні моделі скороченої форми

Скороченою формою структурної моделі є модель, у якій ендогенні змінні виражені як функції лише попередньо визначених змінних. Скорочена форма записується двома способами. Перший – згорнуте вираження ендо­генних змінних як функцій попередньо визначених змінних, наприклад:

Для нашої простої моделі з трьох рівнянь скорочена форма матиме вигляд:

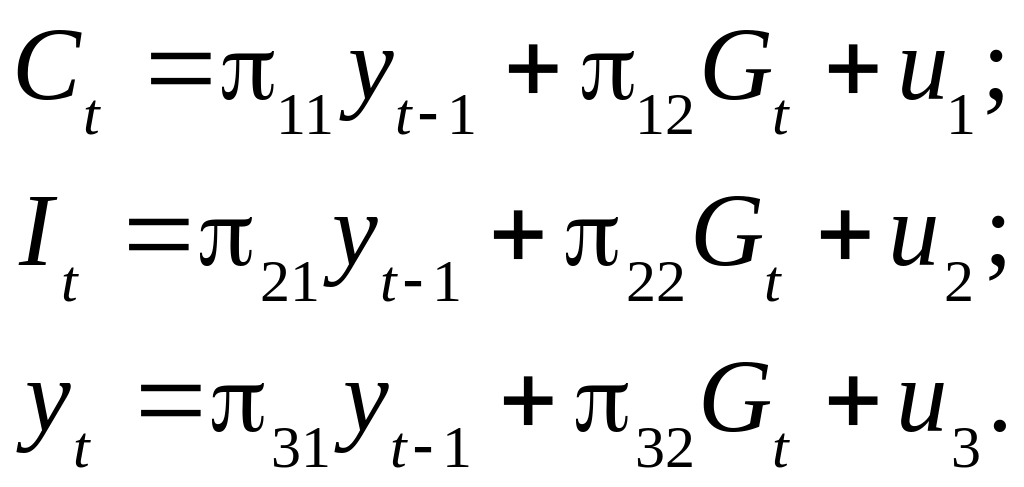
Другий спосіб запису скороченої форми - розгорнуте вираження ен­догенних змінних через попередньо визначені змінні, структурні парамет­ри та випадкові величини. У цьому випадку структурна модель нашого прикладу набуває такого вигляду:

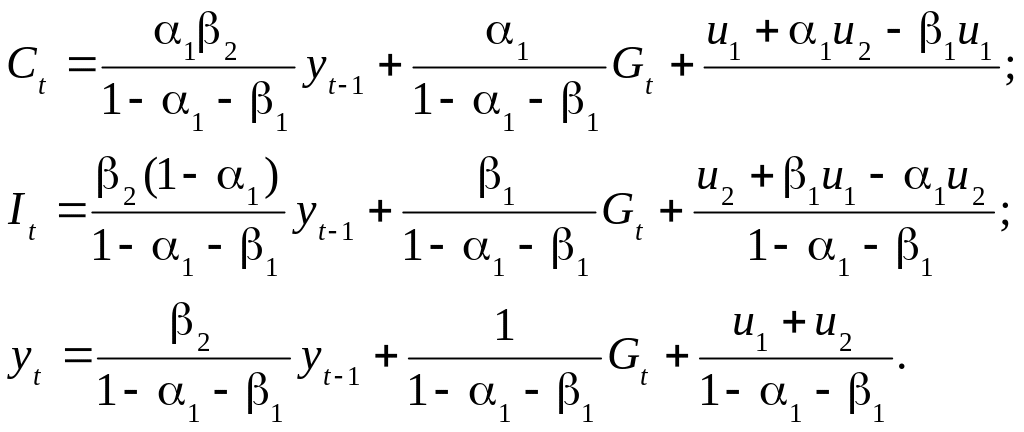
Для збігу двох типів запису скороченої форми необхідно, щоб виконува­лось таке співвідношення між числами п та структурними параметрами:

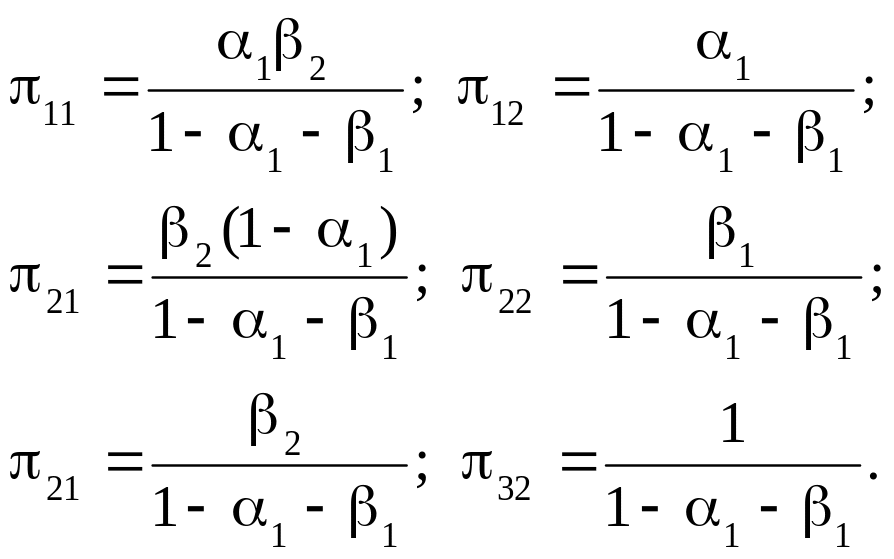
Як бачимо, між параметрами скороченої форми та структурними пара­метрами є чіткий взаємозв’язок, тобто значення є функціями структур­них параметрів.

Параметри скороченої форми вимірюють загальний (прямий та непрямий) вплив попередньо визначених змінних на ендогенні змінні, в той час як структурні параметри вимірюють тільки прямий вплив.

Наприклад, вимірює вплив одиничного зростання на величину інвес­тицій. Цей вплив складається з двох частин: по-перше, є прямий вплив на через коефіцієнт , який визначається в структурному рівнянні інвестицій; по-друге, наявний непрямий вплив, тому що зростання впливає на , впливає неї , яке в свою чергу впливає на ; нарешті значення впливає на , яке в свою чергу впливає на а отже, і на . Тому загальний вплив (що вимірюється ) на можна поділити на такі компоненти:

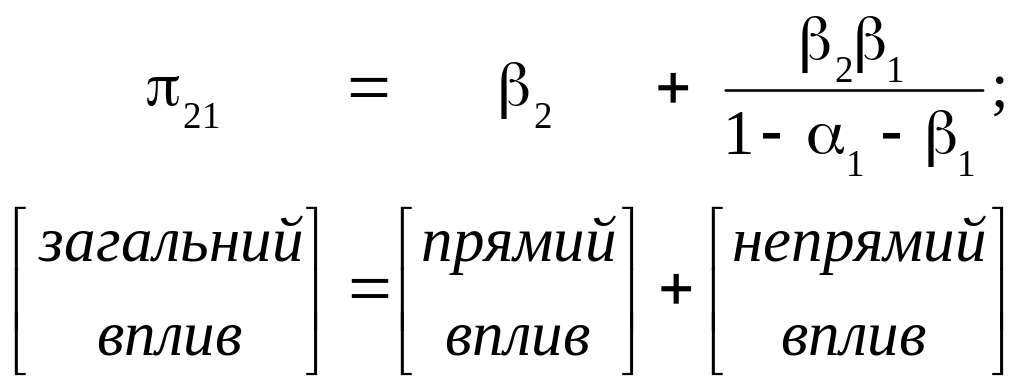
Параметри скороченої форми таким чином можна широко застосову­вати для прогнозування та аналізу економічної діяльності, тому що вони дають одночасно оцінку загального, прямого та непрямого впливу екзо­генних змінних на залежні змінні.

10.5. Проблема ототожнення в симультативних моделях

Як уже зазначалося, в симультативній моделі є змінні двох типів: ендо­генні та попередньо визначені. Ендогенні змінні вважаються стохастичними, тоді як попередньо визначені змінні трактуються як не стохастичні.

Попередньо визначені змінні поділяються на дві категорії: поточні та лагові. Так, наприклад, якщо є поточною екзогенною змінною, то вважається лаговою екзогенною змінною з одиничним лагом. Якщо є ендогенною змінною, то – лагова змінна, значення якої відоме в поточ­ний період часу , отже це значення вважається не стохастичним, а є також попередньо визначеною змінною. Право визначати, які змінні ендо­генні, а які попередньо визначені, належить досліднику, котрий розробляє модель.

Зауважимо, що не всі змінні обов’язково мають з’являтись у кожному рівнянні.

З симультативної (структурної) моделі, як ми вже розглядали вище, можна отримати скорочену форму, в якій ендогенні змінні залежать тільки від попередньо визначених змінних та випадкових величин.

Під проблемою оцінювання параметрів симультативних моделей розуміють знаходження оцінок параметрів на основі оцінених ко­ефіцієнтів скороченої форми. Якщо це можна зробити, то ми маємо право стверджувати, що модель ототожнена. І навпаки.

Ототожнена модель може бути як точно ототожненою, так і переототожненою. Точно ототожнену модель ми маємо в тому разі, коли можна отримати однозначну оцінку її параметрів. Переототожнену модель ми маємо у разі, коли для деяких параметрів структурної моделі є можливість отримати більше ніж одне кількісне значення. Крім того, модель може бути і неототожненою.