10. Економетричні симультативні моделі

10.1. Системи одночасних структурних рівнянь

Застосування методу найменших квадратів (МНК) до окремого рівнян­ня передбачає, що незалежні змінні (фактори) - справді екзогенні і що є тільки односторонній зв’язок між залежною змінною та незалежними змінними . Якщо ці умови не виконуються, тобто, якщо змінні визнача­ються через , то порушується одне з припущень класичного регресійного аналізу, а саме припущення про незалежність факторів та випадкових величин і використання методу найменших квадратів для знаходження невідомих параметрів моделі призведе до появи неефектив­них оцінок з відхиленням.

Якщо і, в свою чергу, також , недопустимо застосовувати одне регресійне рівняння для опису взаємозв’язку між та . У такому разі ми переходимо від регресійної моделі з одним рівнянням до регресійної моделі з багатьма рівняннями, серед яких можуть бути рівняння, які включають та у ролі як ендогенних, так і екзогенних змінних. Система, що описує таку взаємну залежність між змінними, називається системою одночасних або симультативних рівнянь.

10.2. Загальні поняття про методи оцінювання

Як уже зазначалося, застосування методу найменших квадратів при оцінці невідомих параметрів у системах симультативних рівнянь призво­дить до зміщених оцінок. Щоб уникнути цієї неприємної ситуації, необхідне застосування інших методів оцінювання, які давали б кращі оцінки пара­метрів. Такі методи, справді, є. Ось найуживаніші серед них.

1. Метод зменшеної форми, або метод непрямих найменших квад­ратів (ННК).

2. Метод інструментальних змінних (МІЗ).

3. Двокроковий МНК (2МНК).

4. Метод найбільшої вірогідності обмеженої інформації (НВОІ).

5. Метод змішаного оцінювання.

6. Трикроковий МНК (ЗМНК).

7. Метод найбільшої вірогідності повної інформації (НВПІ).

Перші п’ять методів називають методами одного рівняння оскільки вони застосовуються тільки до одного з рівнянь системи. Шостий та сьомий методи (ЗМНК та НВПІ) називають системними методами, оскільки вони застосовуються одночасно до всіх рівнянь системи. Вибір методів для оцінювання параметрів конкретної моделі є непростим завданням. Перед його обговоренням потрібно розглянути декілька визначень і торкнутися проблеми ендогенності й екзогенності певних змінних у конкретних симультативних моделях.

10.3. Попередні відомості про структурні моделі. Ілюстративний приклад

Структурна модель - це повна система рівнянь, що описує структуру взаємозв’язків між економічними змінними. Структурні рівняння вира­жають ендогенні змінні як функції інших ендогенних змінних, поперед­ньо визначених змінних та випадкових величин.

Щоб проілюструвати побудову структурної моделі, використаємо таку просту модель закритої економіки:

Перше рівняння описує функцію споживання, друге – функцію інвести­цій, а трете – основну тотожність. Система завершена, оскільки містить три рівняння з трьома ендогенними змінними – . Модель містить дві попередньо визначені змінні – урядові витрати та доход із запізнен­ням .

Параметри структурної моделі відображають прямий вплив кожного фактора на залежну змінну. За своїм економічним змістом вони можуть бути коефіцієнтами еластичності, граничними нормами та ін. Непрямі впливи можна обчислити тільки при розв’язуванні структурної системи. Наприклад, зміна в споживанні непрямо впливатиме на інвестиції через викликане змінами споживання зростання доходу , який визначає інвестиції.

При побудові структурної моделі вважатимемо, що структурні пара­метри представлені коефіцієнтами , коли вони відносяться до ендоген­них змінних, та коефіцієнтами , коли вони стоять біля попередньо визна­чених змінних. Так само ендогенні змінні позначимо через , а екзогенні змінні через (для спрощення будемо розглядати модель без перетину). Тоді структурна модель матиме вигляд:

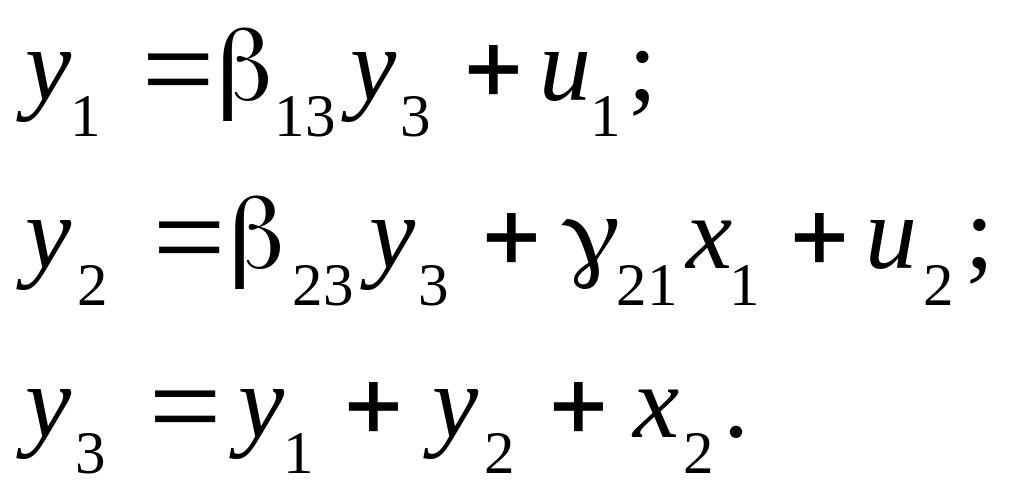
Перенесемо всі змінні у ліву сторону, отримаємо систему рівнянь, з якої легко отримати таблицю структурних параметрів у за­гальному вигляді:

Значення структурних параметрів можна розрахувати, використовую­чи спостереження над змінними моделі та застосовуючи відповідні економетричні методи. Як це робити, ми розглянемо пізніше.