5.8. Коефіцієнти множинної кореляції та детермі­нації

Корисною мірою ступеня відповідності побудова­ної регресії фактичним даним є коефіцієнт множинної кореляції, який визначається як кое­фіцієнт кореляції між та , тобто:

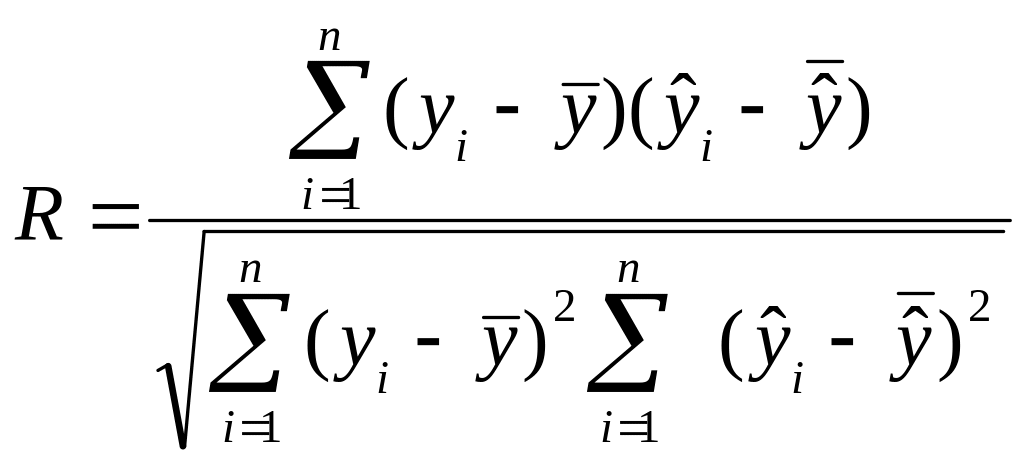
Квадрат коефіцієнта множинної кореляції нази­вають коефіцієнтом детермінації і позначають . Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Можна показати, що й у випадку багатофакторної ре­гресії коефіцієнт детермінації можна подати у вигляді:

, .

5.10. Коефіцієнт детермінації та оцінений кое­фіцієнт детермінації

Важливою властивістю коефіцієнта детермінації є те, що він – не спадна функція від кількості факторів, які входять до моделі. Якщо кількість фак­торів зростає, також зростає і ніколи не зменшуєть­ся. Тобто, якщо ми додаємо новий фактор в регресійну модель, це тільки збільшує значення , що випли­ває з його визначення:

У цьому виразі знаменник не залежить від кількості факторів, тоді як чисельник, навпаки, залежить. Інтуїтивно зрозуміло, що якщо кількість факторів зростає, сума квадратів відхилень спадає (або принаймні не зростає). Якщо ми будемо порівнювати дві регресійні моделі з однаковою залежною змінною, але різною кількістю факторів , то, звичайно, віддамо перевагу тій, яка має більше значення .

Якщо ми хочемо порівняти значення коефі­цієнтів детермінації в різних моделях, ми повинні взяти до уваги кількість факторів у моделях. Для цього вводиться оцінений або скоригований за Тейлом коефіцієнт детермінації, який має вигляд:

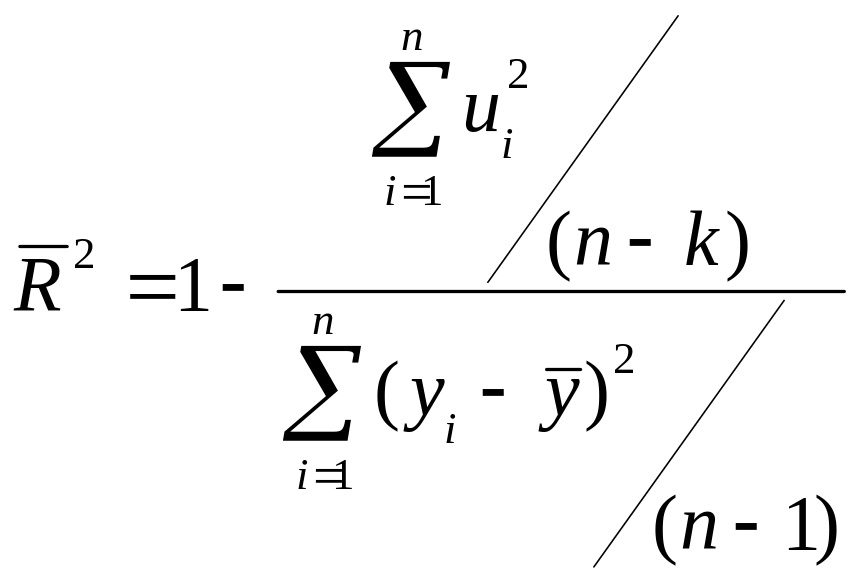
де - кількість параметрів регресійної моделі, вклю­чаючи перетин.

Можна показати, що та пов’язані між собою такою ззалежністю:

З останнього виразу зразу ж випливає: якщо > 1, то < . Крім того, якщо кількість факторів зростає, оцінений коефіцієнт детермінації зменшується порівняно з не оціненим коефіцієнтом. Оцінений коефіцієнт детермінації може бути і від’ємним на відміну від , який має завжди додатне значення. Крім того, коли , оцінений коефіцієнт кореляції також дорів­нює одиниці. Коли прямує до від’ємної величини, прямує до нуля.

5.10. Перевірка моделі на адекватність за f - кри­терієм Фішера

Для перевірки адекватності багатофакторної ре­гресійної моделі, як і у випадку простої лінійної мо­делі, використовується -критерій Фішера.

При цьому нуль-гіпотеза узагальнюється і має вигляд:

проти альтернативної гіпотези – хоча б одне значення відмінне від нуля.

Якщо нуль-гіпотеза неправильна, то тоді пра­вильна гіпотеза , тобто не всі параметри незначно відрізняються від нуля, що дає підставу вважати, що побудована регресійна модель відповідає дійсності, тобто адекватна.

Розраховується -статистика Фішера з та ступенями вільності:

В цій формулі – кількість спостережень та кількість параметрів відповідно.

Фактичне значення даного критерію порівнюється з критичним для заданого рівня значимості . Якщо > , то зі ймовірністю ми стверджуємо, що побудована нами модель є адекватною. Або навпаки, якщо < .