4. Нелінійні моделі та їх лінеаризація

Найбільш популярною моделлю в економіці є лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовуються складніші моделі з нелінійною залежністю між показником та факторами .

За методикою оцінки параметрів нелінійні регресії розглядаються двох видів: 1) нелінійні за факторами, але лінійні за невідомими параметрами, які підлягають оцінці; 2) нелінійні за факторами і параметрами.

Регресії, нелінійні за факторами, але лінійні за оцінюваними параметрами, називаються квазілінійними.

Парну квазілінійну регресію можна записати в загальному вигляді:

Заміною величин нелінійна парна регресія приводиться до лінійної парної регресії: . Тоді для оцінки параметрів використовується МНК і формули набувають вигляду:

, .

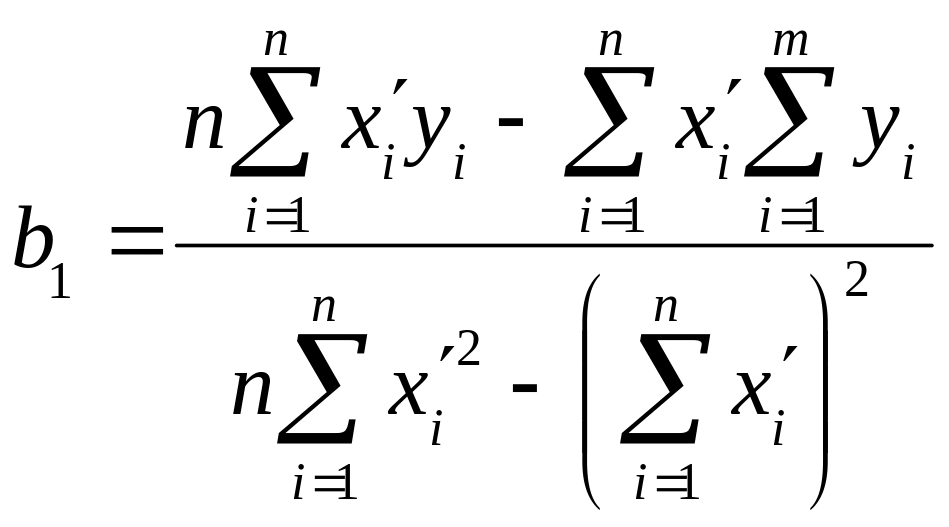Квазілінійну модель з більше ніж одним фактором в загальному вигляді можна записати так:

Якщо, , то .

Приклад.

Гіпербола

Нехай,

Тоді,

Щільністьі нелінійного зв’язку вимірюють з допомогою коефіцієнта детермінації (див. п. 3.8.)

Для оцінки адекватності нелінійних моделей спостережуваним даним можна використовувати критерій Фішера. Перевірка виконується за таким же алгоритмом, що й для лінійної парної регресії (див. п. 3.9.).

Довірчі межі прогнозу для квазілінійної парної регресії оцінюються за тими ж формулами, що й для лінійної парної регресії, лише замість розглядають ( див. п. 3.10.).

В регресіях нелінійних за факторами та параметрами логарифмують праву та ліву частину рівняння і проводять заміну змінних. Таким чином нелінійна регресія зводиться до лінійного виду. Це дає змогу для оцінки параметрів використовувати МНК.

Приклад.

Степенева функція

Про логарифмують праву та ліву частину рівняння:

Нехай,

Тоді,

Показникова функція

Про логарифмують праву та ліву частину рівняння:

Нехай,

Тоді,

Параметри лінійної моделі оцінюють за відомими формулами, використовуючи в якості вихідних даних значення нових змінних – та , якщо потрібно.

Параметри нелінійної моделі знаходять з рівнянь:

.

У тих випадках, коли нелінійна регресія перетворюється в лінійну шляхом логарифмування і заміни змінних, інтервальний прогноз знаходять для відповідної лінійної регресії, а потім, використовуючи зворотні перетворення до меж інтервалів довіри прогнозу лінійної регресії, знаходять межі інтервалів довіри прогнозу нелінійної регресії.

Розглянемо показникову парну регресію:

Для приведення цієї регресії до лінійної, потрібно прологарифмувати праву та ліву частини моделі і зробити заміну змінних:

За формулами, приведеними в пункті 3.10. знаходимо межі інтервальних прогнозів для лінійної регресії, а потім шляхом зворотних перетворень (потенціювання) меж довірчих інтервалів прогнозу для лінійної регресії знаходять межі надійних інтервалів показникової регресії:

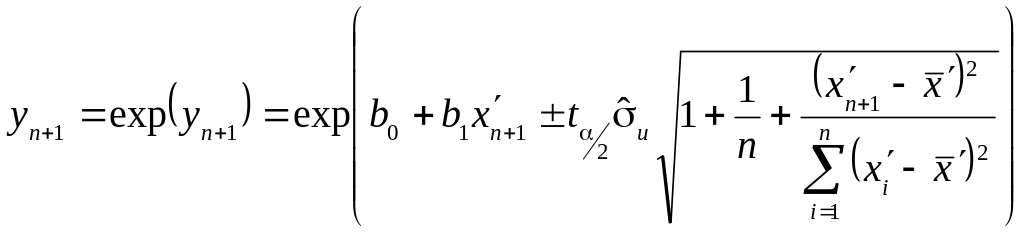
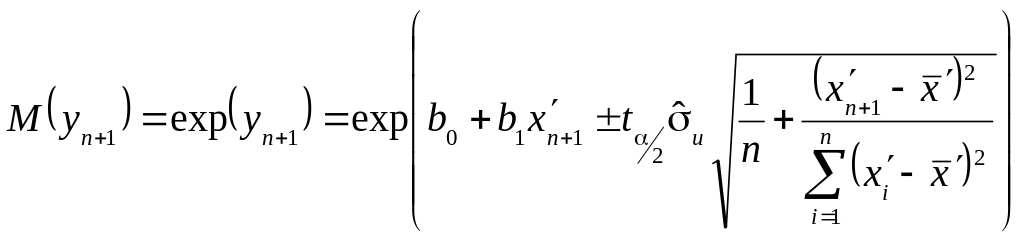
Приклад 2. Нелінійна парна регресія

На основі статистичних даних показника і фактора знайти оцінки параметрів лінії регресії, якщо припустити, що стохастична залежність між ними має вигляд:

Оцінити щільність зв’язку на основі коефіцієнта детермінації. Використовуючи критерій Фішера з надійністю , оцінити адекватність побудованої моделі статистичним даним.

Якщо прийнята математична модель адекватна, то з тією ж надійністю знайти довірчу область базисних даних.

Побудувати графіки фактичних даних, лінії регресії та довірчу область базисних даних.

Таблиця 4.1. Вихідні дані задачі

	1,10	1,55	2,09	2,52	3,07	3,57	4,05	4,56	5,06	5,53
	2,08	6,06	11,65	19,10	29,29	40,10	54,00	70,65	87,53	125,63

Розв’язання

Розглянемо модель виду:

Відповідна вибіркова модель матиме вигляд:

Степенева модель є нелінійною за факторами та параметрами. Для оцінки її параметрів використаємо МНК, але спочатку модель потрібно привести до лінійного виду. Для цього про логарифмуємо праву та ліву частину рівняння:

Нехай,

Тоді,

Ми отримали лінійну модель, що і дає змогу розраховувати оцінки параметрів МНК.

При цьому як вихідну інформацію будемо використовувати значеннями та .

. Лінійна модель матиме вигляд: .

Оскільки , то .

Отже, досліджуваний зв’язок виражатиметься моделлю, що має вигляд:

Знайдемо розрахункові значення (дані розрахунків в табл. 4.2.).

Таблиця 4.2. Розрахункові дані задачі

1	2,08	1,10	0,73	0,10	0,07	0,01	0,87	2,38	1783,46	1808,72
2	6,06	1,55	1,80	0,44	0,79	0,19	1,70	5,45	1533,51	1486,03
3	11,65	2,09	2,46	0,74	1,81	0,54	2,42	11,22	1114,49	1086,30
4	19,10	2,52	2,95	0,92	2,73	0,85	2,87	17,65	727,00	650,71
5	29,29	3,07	3,38	1,12	3,79	1,26	3,35	28,44	261,40	234,67
6	40,10	3,57	3,69	1,27	4,70	1,62	3,71	40,96	13,29	20,33
7	54,00	4,05	3,99	1,40	5,58	1,96	4,02	55,57	120,19	88,19
8	70,65	4,56	4,26	1,52	6,46	2,30	4,30	74,03	865,53	678,13
9	87,53	5,06	4,47	1,62	7,25	2,63	4,56	95,20	2559,84	1842,21
10	125,63	5,53	4,83	1,71	8,27	2,92	4,77	118,01	5387,86	6564,40
	446,09	–	–	-	41,44	14,29	–	–	14366,59	14459,69

Оцінимо щільність зв’язку між залежною змінною та незалежною – , тобто визначимо, наскільки значимим є вплив змінної на .

Коефіцієнт детермінації:

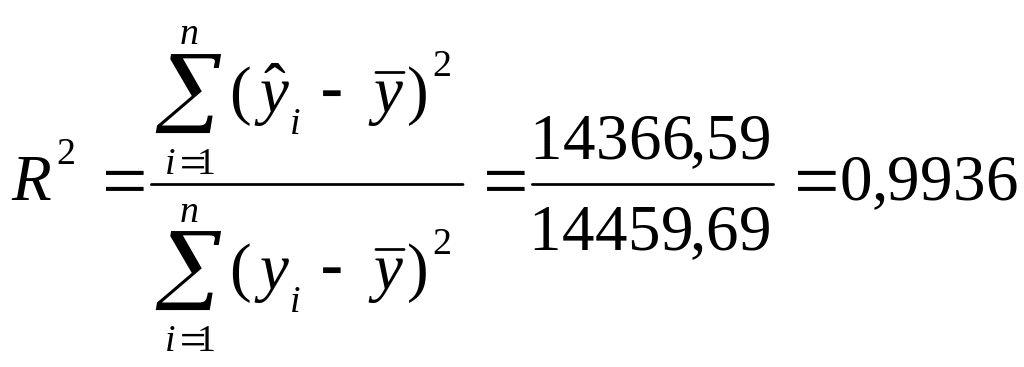
Постільки значення коефіцієнта детермінації близьке до 1, то можна вважати, що побудована модель є адекватною і варіація пояснюється переважно варіацією .

Перевірка моделі на адекватність за –критерієм Фішера:

Розраховуємо величину –критерію:

Задаємо рівень значимості, наприклад, . На цьому етапі за статистичними таблицями –розподілу Фішера з ступенями вільності критичне значення .

Оскільки, , то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною.

Щоб знайти довірчу область базисних даних, за формулами, приведеними в пункті 3.10. знаходимо межі інтервальних прогнозів для лінійної регресії, а потім шляхом зворотних перетворень (потенціювання) меж довірчих інтервалів прогнозу для лінійної регресії знайдемо межі надійних інтервалів для побудованої моделі . Розрахунки представлені в табл. 4.3.

Таблиця 4.3. Розрахункові дані

1	0,73	0,10	0,87	0,0179	0,98	0,23	0,64	1,09	1,90	2,98
2	1,80	0,44	1,70	0,0113	0,42	0,21	1,49	1,90	4,42	6,72
3	2,46	0,74	2,42	0,0014	0,12	0,20	2,22	2,62	9,20	13,70
4	2,95	0,92	2,87	0,0063	0,03	0,20	2,67	3,07	14,50	21,47
5	3,38	1,12	3,35	0,0009	0,00	0,20	3,15	3,54	23,39	34,58
6	3,69	1,27	3,71	0,0005	0,04	0,20	3,52	3,91	33,65	49,86
7	3,99	1,40	4,02	0,0008	0,10	0,20	3,82	4,22	45,56	67,79
8	4,26	1,52	4,30	0,0022	0,19	0,20	4,10	4,51	60,50	90,58
9	4,47	1,62	4,56	0,0071	0,29	0,21	4,35	4,76	77,55	116,88
10	4,83	1,71	4,77	0,0039	0,39	0,21	4,56	4,98	95,80	145,38
	32,56	10,84	–	0,0522	2,54	–	–	–	–	–

Для лінійної моделі .

Нехай, рівень значимості , тоді з ступенями вільності .

Похибку прогнозу обчислюємо за формулою:

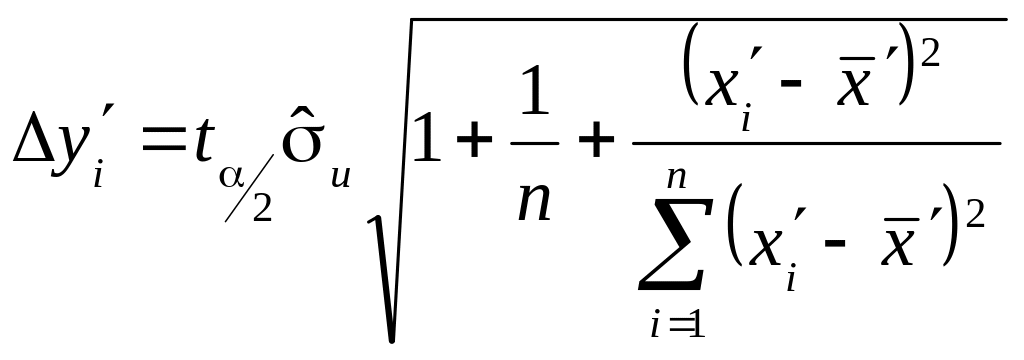
Довірчі зони для знайдемо за формулою:

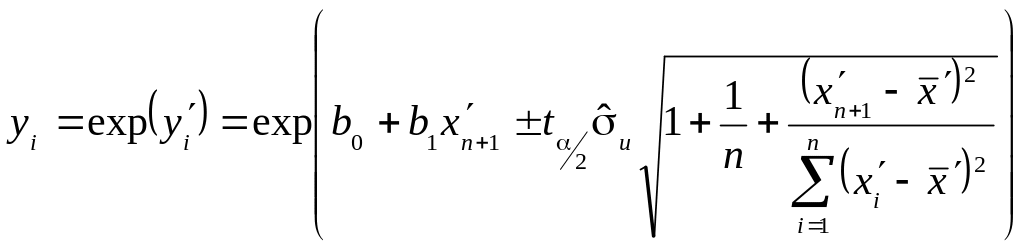
Графіки фактичних даних, лінії регресії та довірча область базисних даних представлені на рис. 4.1.

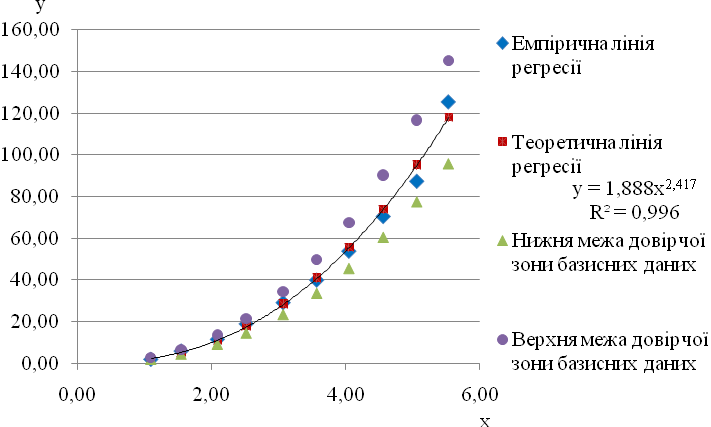
Рис. 4.1. Нелінійна парна регресія залежності від та довірча область базисних даних