3.10. Прогнозування за моделями парної лінійної регресії

Якщо побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної. Прогнози ми можемо отримати двох видів: точковий – дає значення змінної для відповідного значення з побудованої вибіркової моделі: ; інтервальний .

При цьому, виходячи з узагальненої моделі, дійсне значення для прогнозного періоду буде дорівнювати: .

Дійсне значення результату ми знайти не можемо, а можемо лише оцінити його за допомогою прогнозу.

Отже, прогнозне значення є оцінкою дійсного значення змінної . Таким чином з нашої вибіркової моделі ми легко можемо знаходити будь-яке прогнозне значення.

Виходячи з отриманого точкового прогнозу можна побудувати інтервали довіри для його дійсного значення. Такий інтервал довіри при заданому рівні значимості для знаходять за формулою:

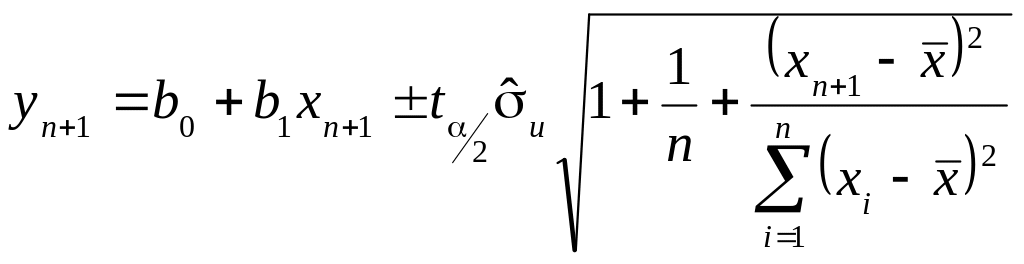
При цьому 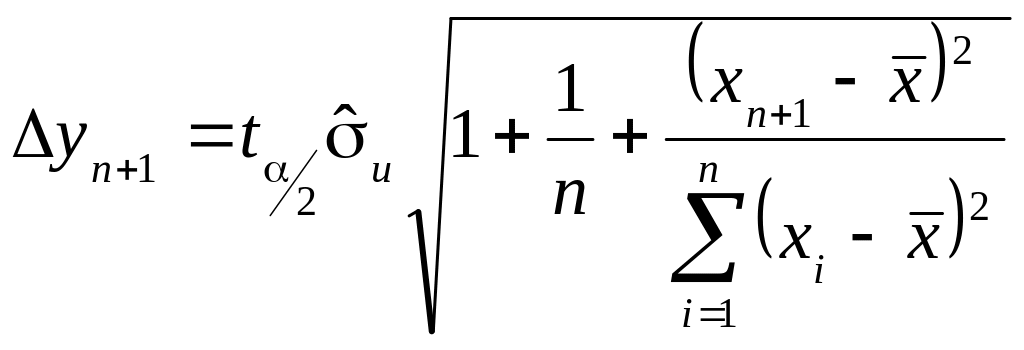– похибка прогнозу.

На практиці більш важлива побудова інтервалів довіри для математичного сподівання , тобто побудова інтервалів довіри для .

В цьому випадку формула модифікується:

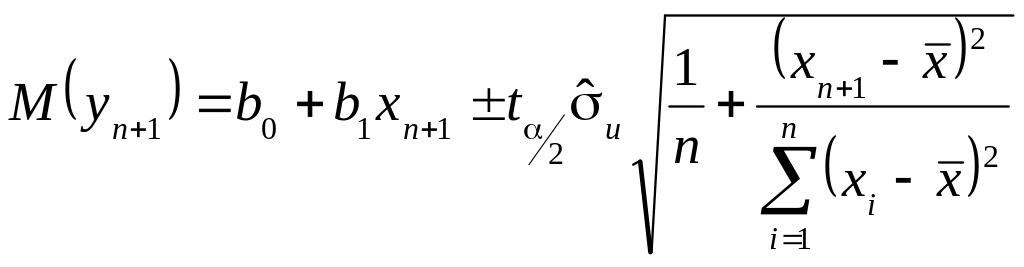
Приклад 1. Лінійна парна регресія

Маємо дані щодо річної продуктивності праці в розрахунку на одного робітника та енергомісткості праці на підприємствах певної галузі. Між цими показниками існує певна залежність. Потрібно перевірити, чи лінійною є залежність між даними показниками, побудувати модель лінійної парної регресії, яка б характеризувала дану залежність; виконати перевірку статистичної значимості оцінок параметрів, знайдених за методом найменших квадратів, та знайти інтервали довіри для параметрів , ; знайти коефіцієнти кореляції та детермінації, за допомогою знайдених коефіцієнтів описати вплив розглядуваного фактору на результат; виконати перевірку моделі на адекватність; знайти інтервальні прогнози для будь-якого значення незалежної змінної.

Таблиця 3.1. Вихідні дані задачі

Номер спостереження	1	2	3	4	5	6	7	8	9	10
, тис. грн.	5,4	5,6	6,2	6,8	7,1	7,8	8,5	9,1	10,5	10,9
, кВт/робітн.	1,8	2,1	2,8	3,0	3,2	3,8	3,9	4,2	4,5	4,8
Номер спостереження	11	12	13	14	15	16	17	18	19	20
, тис. грн.	11,0	11,6	12,1	12,7	13,2	13,9	14,1	14,6	14,9	15,4
, кВт/робітн.	5,2	5,8	5,9	6,2	6,9	7,2	7,5	8,5	8,8	9,4

Розв’язання

Очевидно, що річна продуктивність праці галузі в розрахунку на одного робітника залежить від енергомісткості праці.

Кожну пару спостережень за змінними та можна зобразити у двовимірній системі координат:

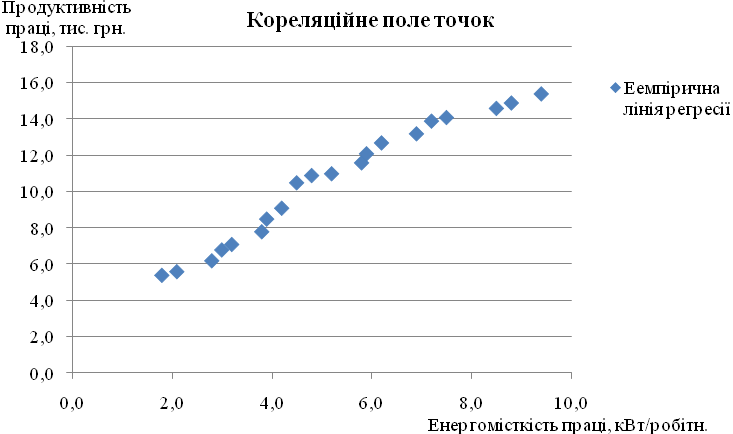
Рис. 3.1. Кореляційне поле точок

Аналіз зображеної множини точок дозволяє зробити висновок про наявність лінійного зв’язку між енергомісткістю та продуктивністю праці, тобто для характеристики даної залежності варто обрати лінійну функцію.

Отже, залежність між енергомісткістю та продуктивністю праці описується простою лінійною моделлю:

де – річна продуктивність праці в розрахунку на одного робітника, тис. грн.; – енергомісткість праці, кВт/робітн.; – стохастична складова, яка вводиться до моделі з метою урахувати наявність впливу факторів, які не входять до моделі, – параметри моделі .

Згідно з гіпотезою про лінійний зв’язок, через кореляційне поле точок можна провести принаймні кілька прямих ліній, які різняться коефіцієнтами та .

Розрахункові значення продуктивності праці можна знайти з вибіркової моделі парної лінійної регресії:

Оцінити параметри моделі та можна, використавши метод 1МНК (розрахунки в табл. 3.2.).

,

; ;

Таблиця 3.2. Розрахункові дані задачі

№ з/п
1	5,4	1,8	9,7	3,2	5,6	0,0	26,7	12,1	17,97	25,0
2	5,6	2,1	11,8	4,4	6,0	0,2	24,7	10,1	15,78	20,9
3	6,2	2,8	17,4	7,8	7,0	0,7	19,1	6,1	10,82	12,7
4	6,8	3,0	20,4	9,0	7,3	0,2	14,2	5,2	8,58	10,7
5	7,1	3,2	22,7	10,2	7,6	0,2	12,0	4,3	7,20	8,9
6	7,8	3,8	29,6	14,4	8,4	0,4	7,7	2,2	4,09	4,5
7	8,5	3,9	33,2	15,2	8,6	0,0	4,3	1,9	2,85	3,9
8	9,1	4,2	38,2	17,6	9,0	0,0	2,2	1,2	1,58	2,4
9	10,5	4,5	47,3	20,3	9,5	1,1	0,0	0,6	0,05	1,2
10	10,9	4,8	52,3	23,0	9,9	1,0	0,1	0,2	-0,16	0,5
11	11,0	5,2	57,2	27,0	10,5	0,3	0,2	0,0	-0,03	0,0
12	11,6	5,8	67,3	33,6	11,3	0,1	1,1	0,3	0,54	0,6
13	12,1	5,9	71,4	34,8	11,5	0,4	2,3	0,4	0,96	0,8
14	12,7	6,2	78,7	38,4	11,9	0,6	4,5	0,9	1,97	1,8
15	13,2	6,9	91,1	47,6	12,9	0,1	6,9	2,6	4,27	5,5
16	13,9	7,2	100,1	51,8	13,3	0,3	11,1	3,7	6,41	7,7
17	14,1	7,5	105,8	56,3	13,8	0,1	12,5	5,0	7,85	10,3
18	14,6	8,5	124,1	72,3	15,2	0,4	16,2	10,4	13,00	21,6
19	14,9	8,8	131,1	77,4	15,6	0,6	18,7	12,4	15,26	25,8
20	15,4	9,4	144,8	88,4	16,5	1,2	23,3	17,0	19,92	35,3
Сума	211,4	105,5	1254,0	653,0	-	7,9	207,9	96,5	138,91	200,0

Модель лінійної парної регресії має вигляд:

Оскільки вільний член , то величина продуктивності праці не є строго пропорційною до енергомісткості праці. Кількісна оцінка параметра показує, що граничне збільшення продуктивності праці при зростанні енергомісткості на 1 кВт/робітн. становить 1,44 тис. грн.

Виконаємо перевірку істотності або статистичної значимості оцінок параметрів моделі за допомогою t -критерію Стьюдента:

; ;

;

;

Критичне значення критерію Ст’юдента для рівня значимості та ступенів вільності ( – кількість параметрів ) знаходимо за допомогою таблиць –розподілу Ст’юдента (дод. А): .

Оскільки, < , то оцінка вважається статистично значимою, тобто, зі ймовірністю 95% вплив рівня енергомісткості праці на продуктивність праці визнається істотним. < , то оцінка також вважається статистично значимою зі ймовірністю 95%.

Довірчі межі коефіцієнта регресії зі ймовірністю 0,95:

або

Довірчі межі вільного члена зі ймовірністю 0,95:

або

Для оцінки щільності зв’язку обчислимо лінійний коефіцієнт кореляції Пірсона.

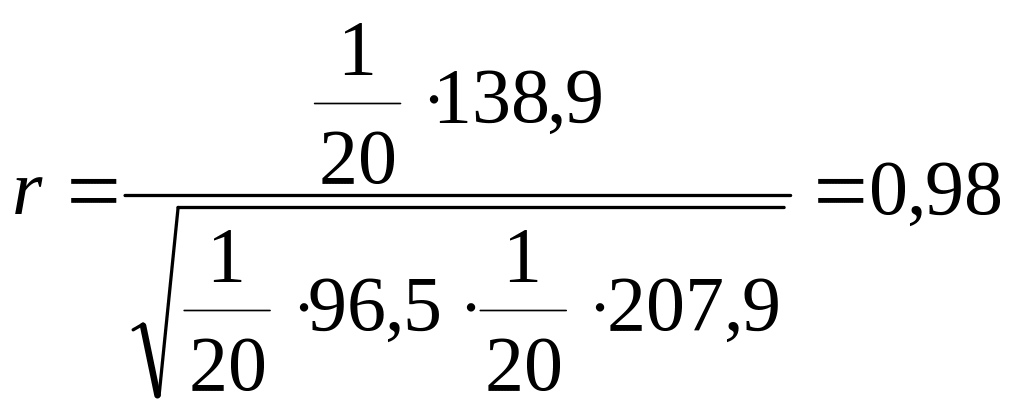
Значення лінійного коефіцієнта кореляції 0,98 близьке до одиниці, тому можна зробити висновок про досить тісний прямий ( ) зв’язок між енергомісткістю та продуктивністю праці.

Коефіцієнт детермінації використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної:

Або Постільки значення коефіцієнта детермінації близьке до одиниці, то можна вважати, що побудована модель адекватна.

Виконаємо перевірку моделі на адекватність за –критерієм Фішера:

Розраховуємо величину –критерію:

Задаємо рівень значимості: .

За статистичними таблицями –розподілу Фішера з ступенями вільності та рівнем значимості знаходимо критичне значення критерію: (дод. В). , то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною.

Оскільки побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Нехай, , тоді точковий прогноз:

Інтервал довіри при заданому рівні значимості для індивідуального значення :

Зі ймовірністю 0,95 при енергомісткості річна продуктивність праці в галузі буде не меншою за 15,79 тис. грн. і не більшою 18,95 тис. грн.

Інтервал довіри для математичного сподівання :

На рис. 3.1. зображено емпіричну лінію регресії, теоретичну лінію регресії та довірчу область прогнозних значень для базисних даних значень .

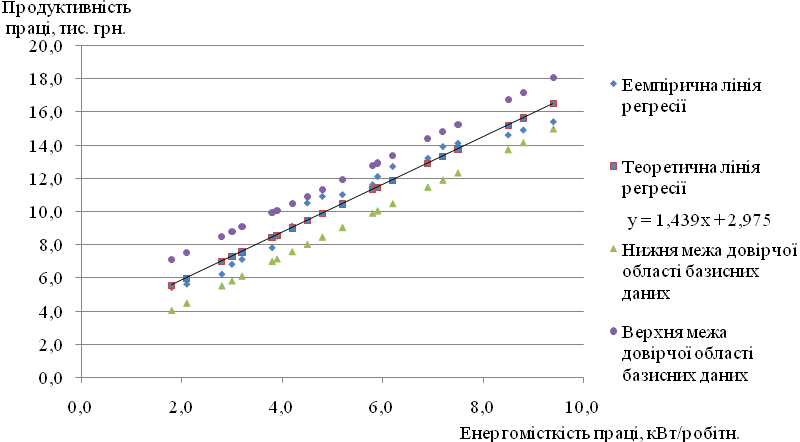
Рис. 3.2. Лінійна парна регресія залежності річної продуктивності галузі від енергомісткості та довірча область базисних даних