3.8. Коефіцієнт детермінації

Вимірювання щільності нелінійного зв’язку ґрунтується на співвідношенні варіацій теоретичних та емпіричних значень результативної ознаки. Відхилення індивідуального значення ознаки від середньої можна розкласти на дві складові. У регресійному аналізі це відхилення від лінії регресії та відхилення лінії регресії від середньої .

Відхилення є наслідком дії фактора , відхилення – наслідком дії інших факторів. Взаємозв’язок факторної та залишкової варіації описується правилом декомпозиції варіацій: загальну дисперсію результативної ознаки можна розкласти на дві частини - дисперсію, що пояснює регресію, та дисперсію помилок:

де – загальна дисперсія; – факторна дисперсія; – залишкова дисперсія, або дисперсія помилок.

Очевидно, значення факторної дисперсії буде тим більшим, чим сильніший вплив фактора та .

Поділивши обидві частини на загальну дисперсію, отримаємо:

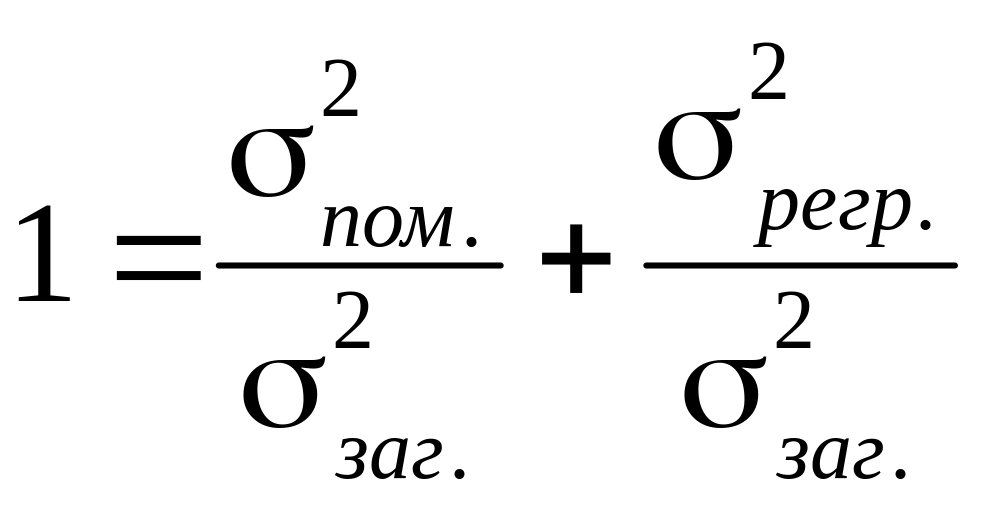
Перша частина цього виразу являє собою частину дисперсії, яку не можна пояснити через регресійний зв’язок, друга - частину дисперсії, яку можна пояснити, виходячи з регресії. Вона називається коефіцієнтом детермінації і використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної:

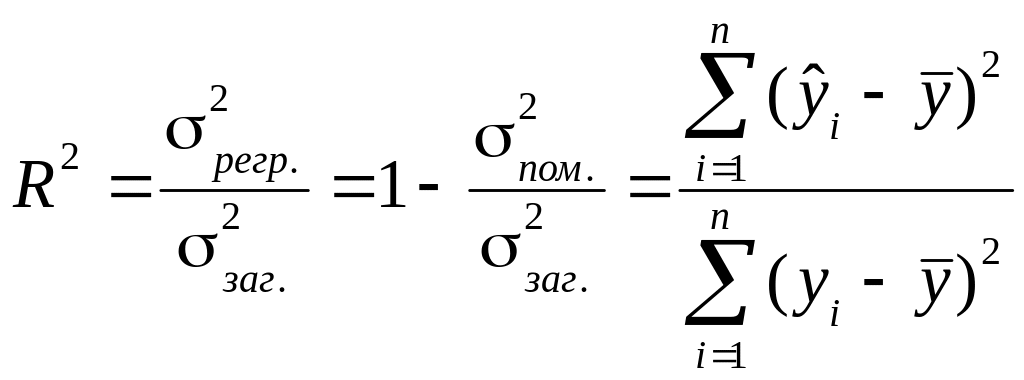
Для лінійного зв’язку: .

Якщо значення коефіцієнта детермінації близьке до одиниці, то можна вважати, що побудована модель адекватна ( ). Варіація на залежить від варіації , і на від варіації інших факторів, які не враховуються в моделі.

3.9. Перевірка парної лінійної регресії на адекватність за –критерієм Фішера

При аналізі лінійної моделі на адекватність необхідно детально проаналізувати похибку спостереження:

– якщо похибка двічі змінює свій знак, то лінійна модель не адекватна;

– якщо похибка від виміру до виміру систематично зростає або спадає, то лінійна модель також є не адекватною.

Адекватність простої лінійної регресійної моделі можна перевірити за до­помогою коефіцієнта детермінації. Якщо його зна­чення близьке до одиниці, то можна вважати, що мо­дель адекватна. Якщо його значення близьке до нуля, то модель неадекватна, тобто немає лінійного зв’язку залежною та незалежною змінними. Але який висновок можна зробити, якщо значення коефіцієн­та кореляції має не явно виражене граничне значен­ня, наприклад, 0,5; 0,45; 0,44 і т.ін.? Зрозуміло, що в таких випадках важко зробити однозначний висновок про наявність зв’язку, тобто про адекватність моделі. Нам потрібен інший критерій, який би однозначно давав відповідь на запитання про адекватність побудованої моделі. Найбільш поширеним із таких критеріїв є критерій Фішера.

Перевірка моделі на адекватність за –критерієм Фішера складається з таких етапів:

1. Розраховуємо величину –критерію:

В цій формулі – кількість спостережень та кількість параметрів відповідно.

2. Задаємо рівень значимості, наприклад, . Тобто, ми вважатимемо, що можлива помилка для нас становить 0,05, це означає, що ми можемо помилитися не більш, ніж у 5% випадків, а в 95% випадків наші висновки будуть правильними.

3. На цьому етапі за статистичними таблицями –розподілу Фішера з ступенями вільності та рівнем значимості знаходимо критичне значення . Якщо < , то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною. Або навпаки, якщо > .