Оцінок параметрів та , знайдених за мнк

Параметри регресії у невеликих за обсягом сукупностях здатні до випадкових коливань. Тому здійснюють перевірку їх істотності або статистичної значимості за допомогою –критерію Ст’юдента.

Можна показати, що параметри, знайдені за МНК, розподілені за нормаль­ним законом розподілу, що формалізовано можна записати таким чином:

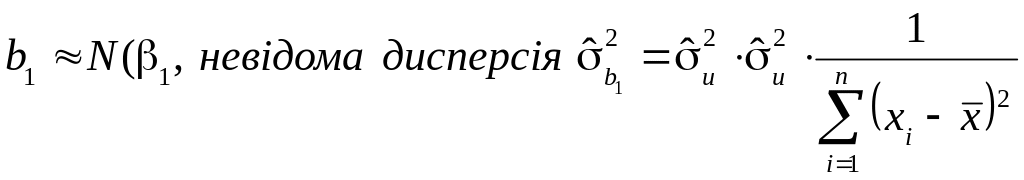
В загальному випадку дисперсії оцінок параметрів не­відомі, тому що не можна обчислити , бо випадкові величини взагалі є не спостережуваними. Але ми можемо обчислити оцінку дисперсій , тобто знайти:

,

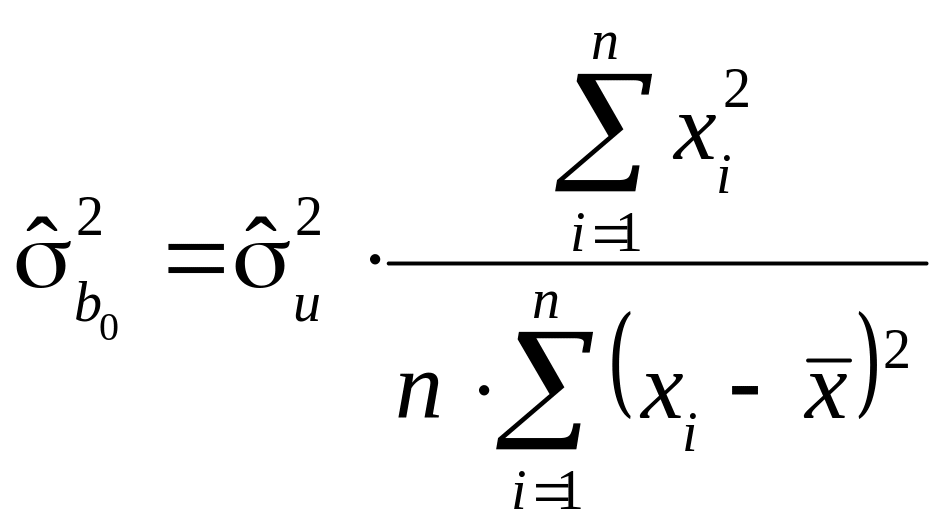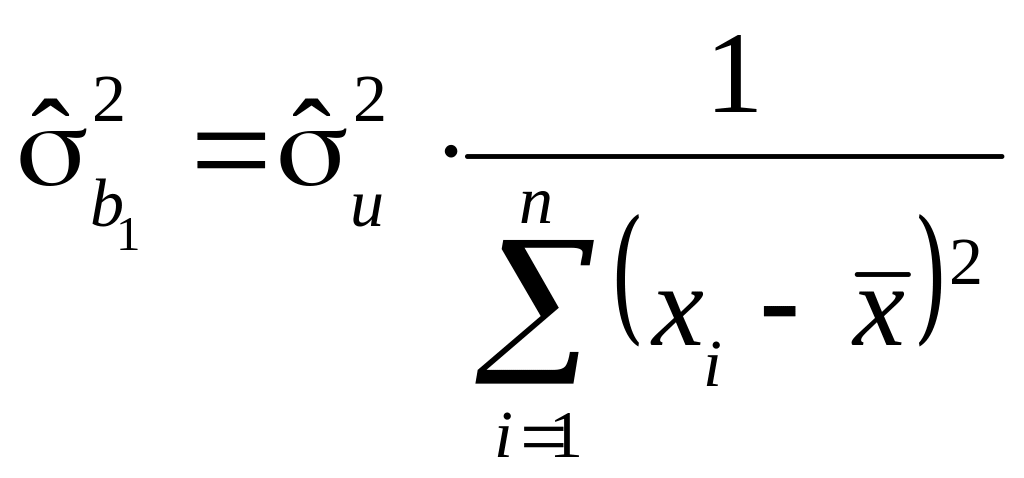
де , – кількість оцінених параметрів.

А потім побудувати –статистику для кожного параметра:

,

з ступенями вільності, де – оцінка параметра , отримана за МНК; – гіпотетичне значення, яке має набути параметр ; оцінки дисперсій параметрів відповідно.

В економетрії поширеною формою нуль-гіпотези є така: проти альтернативної .

В цьому разі –статистика для параметрів має вигляд:

Критичне значення критерію Ст’юдента для рівня значимості (задається дослідником) та ступенів вільності ( – кількість параметрів ) знаходимо за допомогою таблиць –розподілу Ст’юдента. Якщо < , то оцінка вважається статистично значимою.

3.6. Інтервали довіри для параметрів та

Для того щоб визначити, як параметри та пов’язані з їх оцінками та , потрібно побудувати інтервали довіри для параметрів узагальненої регресійної моделі, тобто такі інтервали, в які з заданою ймовірністю потрапляють їхні значення.

Процедура побудови інтервалів довіри є аналогічною процедурі тестування значимості знайдених параметрів простої вибіркової лінійної регресії. Спочатку обираємо рівень значимості ( або ), відповідно рівень довіри буде дорівнювати або . За - таблицею Ст’юдента знаходи­мо значення з ступенями вільності. Тоді можемо записати:

– довірчі межі коефіцієнта регресії : зі ймовірністю ;

– довірчі межі вільного члена: зі ймовірністю .

3.7. Оцінка щільності та перевірка істотності кореляційного зв’язку

Поряд з визначенням характеру зв’язку важливе значення має оцінка щільності зв’язку, тобто оцінка узгодженості варіації взаємозв’язаних показників. Якщо вплив факторного показника на результативний значний, то це виявиться в закономірній зміні значень результативного показника зі зміною значень факторного, тобто фактор своїм впливом формує варіацію . За відсутності зв’язку варіація не залежить від варіації .

Для оцінювання щільності зв’язку використовують низку коефіцієнтів з такими спільними властивостями:

1. За відсутності будь-якого зв’язку значення коефіцієнта наближається до нуля; при функціональному зв’язку – до одиниці.

2. За наявності кореляційного зв’язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв’язок.

Серед мір щільності зв’язку найпоширенішим є коефіцієнт кореляції Пірсона. Сфера його використання обмежується лінійною залежністю. Обчислення лінійного коефіцієнта кореляції ґрунтується на аналізі відхилень значень взаємозв’язаних ознак та від середніх.

За наявності прямого кореляційного зв’язку будь-якому значенню > відповідає значення > , а < відповідає < .

Коефіцієнт кореляції визначається відношенням зазначених сум:

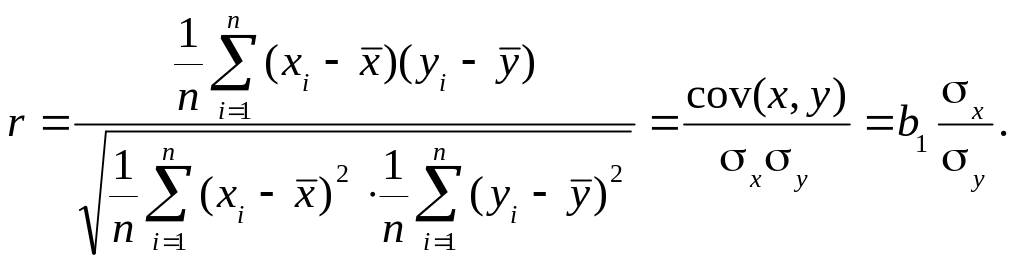
В разі функціонального зв’язку фактична сума відхилень дорівнює граничній, а коефіцієнт кореляції При кореляційному зв’язку абсолютне його значення буде тим більшим, чим щільніший зв’язок. Якщо значення лінійного коефіцієнта кореляції близьке до 1 і >0 , то можна зробити висновок про досить тісний прямий зв’язок між та . І навпаки. Якщо <0, то зв’язок між ознаками зворотній.