Задача №14

Частица массы m падает слева на потенциальный барьер высотой U. (рис. 7). Энергия частицы равна Е, причем Е > U. Найти эффективную глубину х_эф проникновения частицы под барьер, т.е. расстояние от границы барьера до точки, в которой плотность вероятности P нахождения частицы уменьшается в е раз. Вычислить х_эф для электрона, если U - E = 1,0 эВ.

В данном случае вид уравнений Шредингера и ψ – функций будет совпадать со случаем, когда Е > U (см. задача №13 формулы (22) – (25)), однако k₂, будет чисто мнимым

,

где i – мнимая единица, ,

тогда плотность вероятности P(x) местоположения частицы в области II будет равна

.

Плотность вероятности нахождения частицы в точке х = 0

.

Отсюда

.

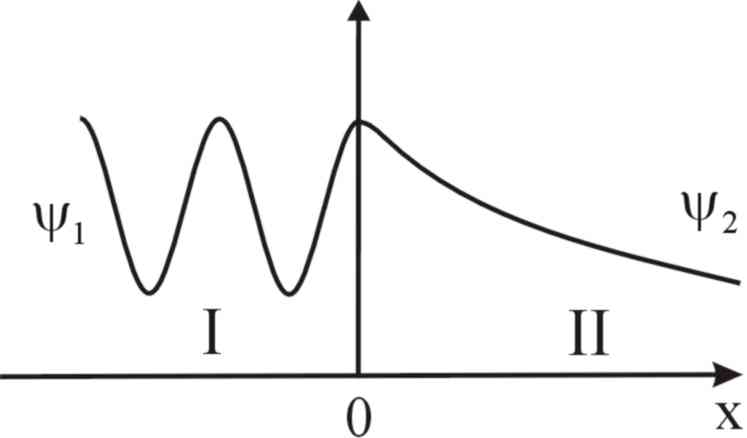
Качественный вид  - функций в областях I и II показан на рис. 8.

Т.к. эффективная глубина проникновения частицы определяется как расстояние, на котором плотность вероятности местонахож-

Рис. 8 дения частицы уменьшается в е раз то

.

Отсюда

.

Подставив численные значения, получим .

Задача №15

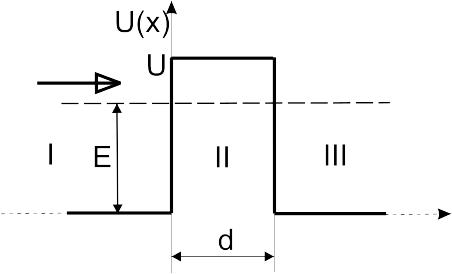
Частица с энергией Е = 50 эВ падает слева на прямоугольный барьер, бесконечной ширины высотой U = 20 эВ (рис 7). Определите вероятность отражения частицы от этого барьера.

Как было показано в предыдущей задаче, коэффициент отражения R равен

,

где k₁ и k₂ – волновые числа волн де Бройля в областях I и II.

Поскольку

.

Отсюда

.

Задача №16

Электрон с энергией Е = 4,9 эВ движется в положительном направлении оси х. Высота U потенциального барьера равна 5 эВ. При какой ширине барьера d вероятность P прохождения электрона через него будет равна 0,2?

Вероятность P прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности D. Тогда

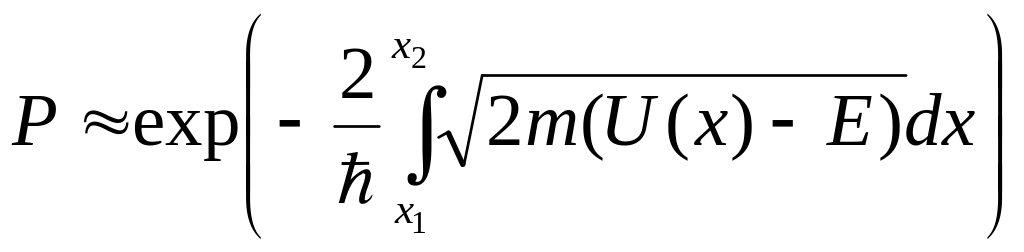. (27)

Рис. 9 Так как для данного барьера (Рис. 9) U(x) = U, х₁ = 0, х₂ = d, то (27) примет вид

.

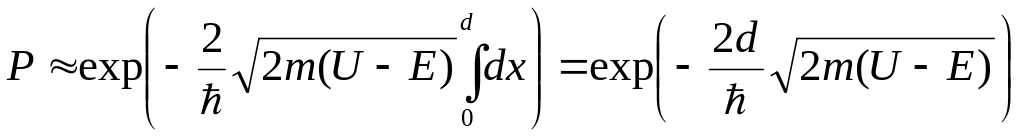Потенцируя это выражение, получим

.

Отсюда

.

Произведя вычисления, получим d = 0.495 нм.

Задача №16

Найти вероятность прохождения частицы массой m с энергией Е сквозь потенциальный барьер, показанный на рис. 10.

П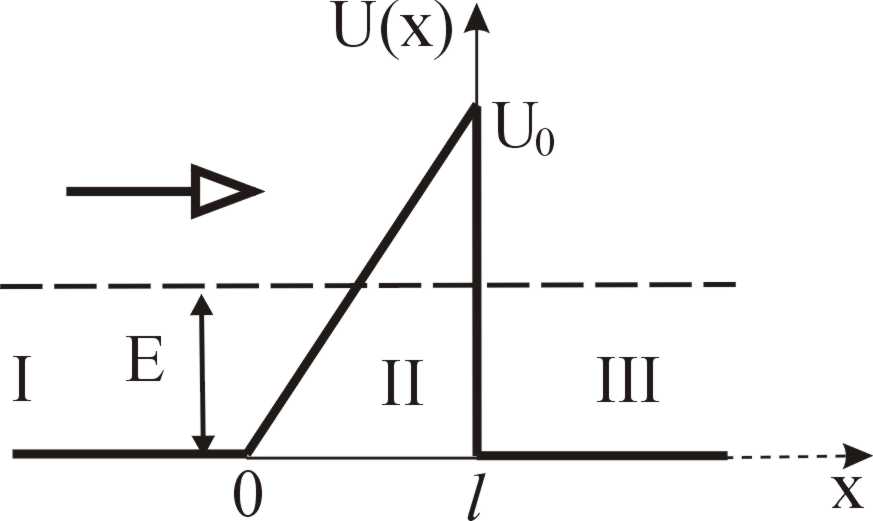 о аналогии с предыдущей задачей

. (28)

В данном случае (рис.10)

, , х₂ = l,

Рис.10 тогда (28) примет вид

.

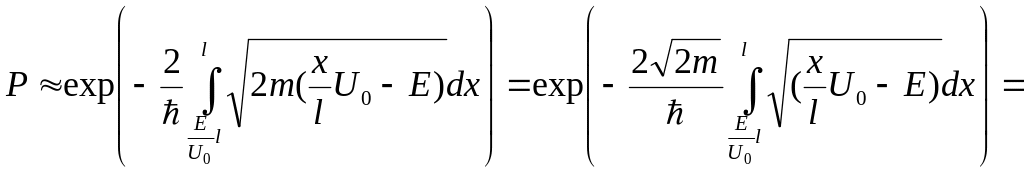
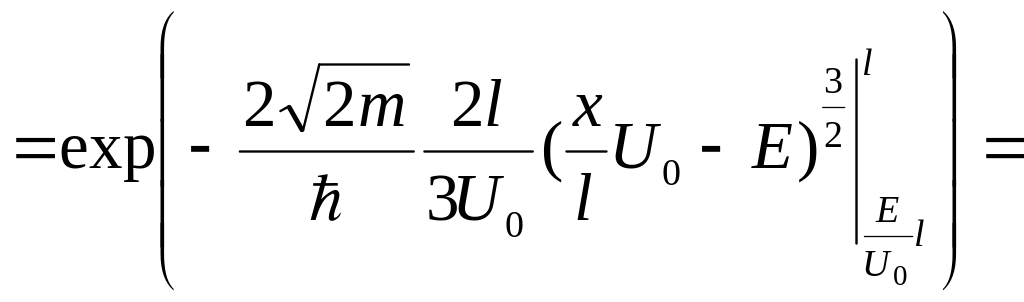
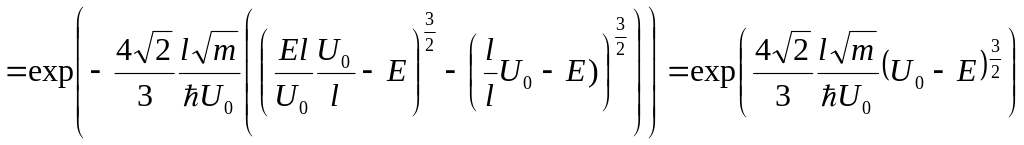ОСНОВНЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ

Постоянная Планка
Скорость света в вакууме	с = 2,998108 м/c
Масса электрона
Заряд электрона
Электрическая постоянная	o = 8,8510-12 Ф/м 1/4o=9109 м / Ф
Постоянная Ридберга

ЛИТЕРАТУРА

1. Иродов И.Е. Задачи по квантовой физике: Учебное пособие для физ. спец. вузов. – М.: Высшая шк., 1991. – 175с.

2. Иродов И.Е. Квантовая физика. Основные законы: Учебное пособие для вузов. – М.: Лаборатория Базовых Знаний, 2001. – 271с.

3. Трофимова Т.И., Павлова З.Г.: Сборник задач по курсу физики с решениями: Учебное пособие для вузов. Изд. седьмое, стереотипное– М.: Высшая шк., 2006. – 591с.

4. Чертов А.Г, Воробьев А.А. Задачник по физике. Изд. пятое, переработанное и дополненное – М.: Высшая шк., 1988. – 527с.

5. Борн М. Атомная физика. – М.: «Мир», 1970. – 483с.

6. Савельев И.В. Курс общей физики. Т.3 - М.: Наука., 1982. – 304с.

7. Савельев И.В. Сборник вопросов и задач по общей физики. - М.: Наука, 1982. –271с.

24