Задача №11

Частица находиться в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Найти вероятность пребывания частицы в области l/3<x<2l/3 а) если частица находиться в основном состоянии; б) если частица находиться в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения частицы в данном состоянии.

а) - функция в основном состоянии (n = 1) имеет вид:

.

Тогда искомая вероятность

.

Графически плотность вероятности обнаружения частицы в данном состоянии изображена на рис. 5

б) в данном случае -функция будет иметь следующий вид

Графически плотность вероятности обнаружения частицы в данном состоянии изображена на рис. 6

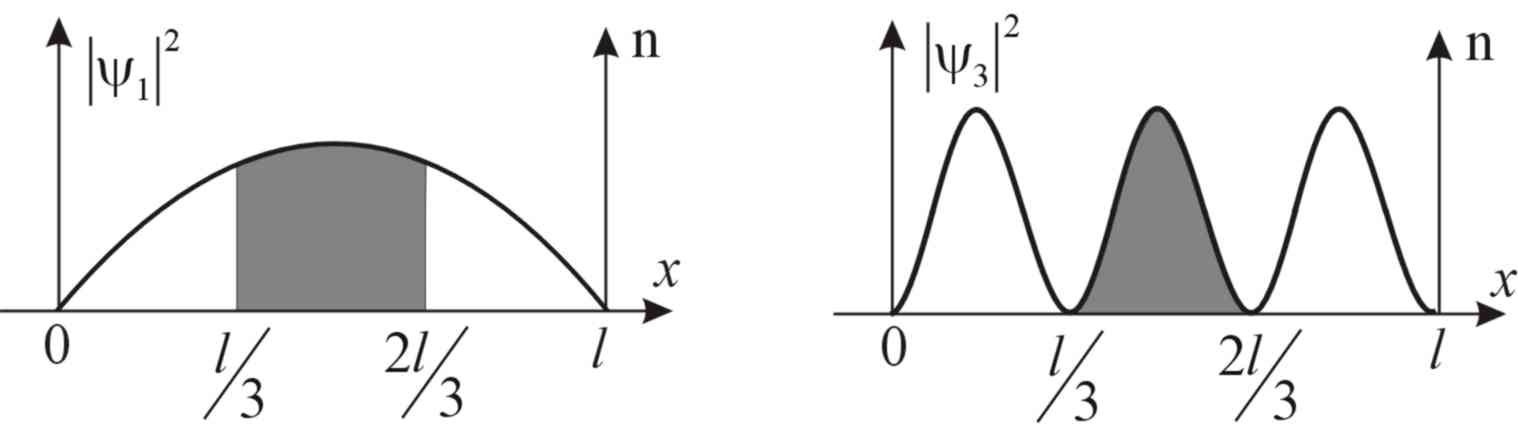
Рис.5 Рис.6

Задача №12

Пси-функция некоторой частицы имеет вид , где r – расстояние от силового центра, а – константа. Найти: а) значение константы А, б) среднее расстояние <r> частицы от центра.

Значение константы А найдем из условия нормировки пси-функции

,

где dV =4r²dr– объем тонкого сферического слоя толщиной dr, находящегося на расстоянии r от центра. Тогда условие нормировки принимает вид

.

Отсюда

.

Как известно, среднее значение величины q, зависящей от координат

.

Тогда .

Задача №13

Частица массы m с энергией равной Е движется в положительном направлении оси х и встречает на своем пути бесконечно широкий потенциальный барьер высотой U., причем Е > U (рис.7) Для областей I и II: а) запишите уравнение Шредингера б) представьте графически качественный вид ψ – функций. Найти коэффициент отражения R и коэффициент прозрачности этого барьера.

Д ля данного барьера

.

На барьер падает частица массы m энергия которой Е, исходя из волновых представлений на барьер падает дебройлевская волна

Рис. 7 .

Поскольку у всех трех волн (падающей, отраженной и прошедшей) частота одинакова, т.к. , то ограничимся рассмотрением только координатной части, а именно (x).

Запишем уравнения Шредингера для областей I и II

где ; (22)

где . (23)

Решением этих уравнений будут следующие функции:

; (24)

; (25)

Падающая волна характеризуется амплитудой a₁, отраженная – b₁ , прошедшая – а₂. Поскольку в области x > 0 имеется только прошедшая волна, то b₂ = 0.

Из условия непрерывности для  и  ^/ в точке x = 0 следует

,

.

Решая совместно эти уравнения, получим

, . (26)

Обычно  - функция нормируется таким образом что а₁ = 1, тогда

.

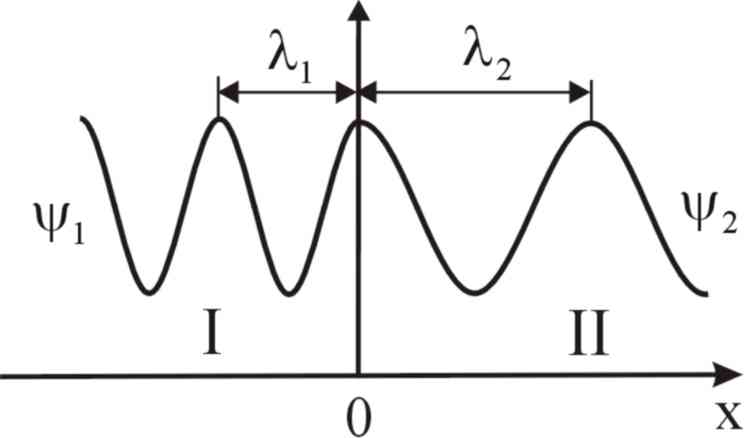
Качественный вид  - функций в областях I и II показан на рис. 8

Рис. 8

Для определения интересующих нас коэффициентов отражения R и прозрачности D введем понятие потока плотности вероятности . Скорость распространения вероятности такого потока совпадает со скоростью частицы

.

Таким образом v  k и плотность потока вероятности пропорциональна величине kψψ^*. В соответствии с видом ψ – функции для падающей, отраженной и прошедшей волн имеем

   ^/   ^//  .

Учитывая (26) получим следующие выражения для коэффициентов R и D:

, .

Отсюда следует, что R + D = 1, что и должно быть по определению. Анализ выражений, полученных для R и D, показывает, что значения R и D не зависят от направления движения частицы. Заметим, что в классическом случае при Е>U R = 0.