Задача №9
Найти решение временного уравнения Шредингера для свободной частицы, движущейся с импульсом p в положительном направлении оси x.
Поскольку в данном случае потенциальная энергия частицы равна нулю U(x) = 0, то уравнение Шредингера будет иметь следующий вид:
. (14)
Решение данного уравнения будем искать методом разделения переменных, т.е. представим в виде произведения двух функций, одна из которых зависит только от координаты x, а другая – только от времени t.
. (15)
Подставляя (15) в (14) получим
или
,
(16)
где
.
Т.к. обе части уравнения (16) являются функциями независимых переменных, то равенство правой и левой его частей возможно лишь тогда, когда они равны одной и той же константе. Из сравнения уравнения (16) со стационарным уравнением Шредингера можно видеть, что этой константой является E. Тогда
Общие решения данных дифференциальных уравнений должны иметь следующий вид (в этом нетрудно убедиться их непосредственной подстановкой):
,
где
;
,
где
.
Тогда для частицы, движущейся в положительном направлении вдоль оси х, искомое решение уравнения (1) будет иметь вид
.
(17)
Данное решение будет конечным при Е > 0, причем Е в этом случае может быть любым. Волна, описываемая уравнением (17), имеет вид дебройлевской.
Плотность
вероятности местоположения частицы
.
Это означает равновероятность нахождения
частицы в любой точке пространства (оси
х).
Данный вывод хорошо согласуется с
соотношением неопределенностей: при
px
= 0 x
,
т.е. частица «размазана» по всему
пространству.
Задача №10
Частица массы m находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Показать, что собственные значения энергии частицы и ее нормированные собственные функции (0 < х < l) имеют вид
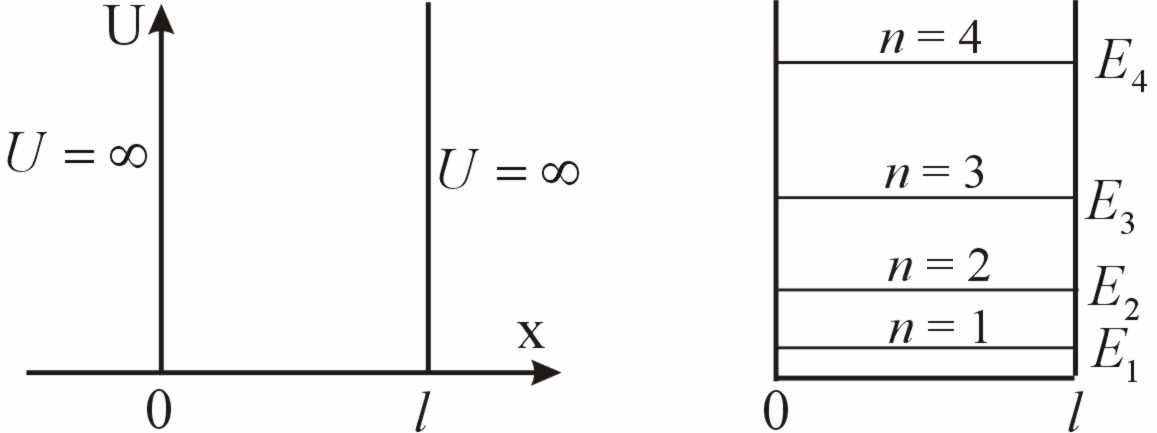
Рис.3 Рис.4
Стационарное уравнение Шредингера в одномерном случае имеет вид:
. (18)
В области 0 < х < l потенциальная энергия равна нулю U = 0 (рис. 3), тогда
Введя
следующее обозначения
,
получим
. (19)
Полученное дифференциальное уравнение хорошо известно из теории колебаний. Решение такого уравнения имеет вид:
.
(20)
За пределами ямы (x) = 0. Поскольку функция (x) должна быть непрерывна, то она должна обращаться в ноль на границах ямы (0)= (l)=0. Следовательно,
,
где (n
= 1, 2, 3…).
(21)
(Случай n = 0 отпадает, потому что тогда 0, т.е. частица нигде не находится).
Учитывая
введенное нами обозначение:
,
откуда
(n
= 1, 2, 3…)
т.е. спектр энергии дискретный. Подставив (21) в (20), получим
Для нахождения коэффициента А воспользуемся условием нормировки
.
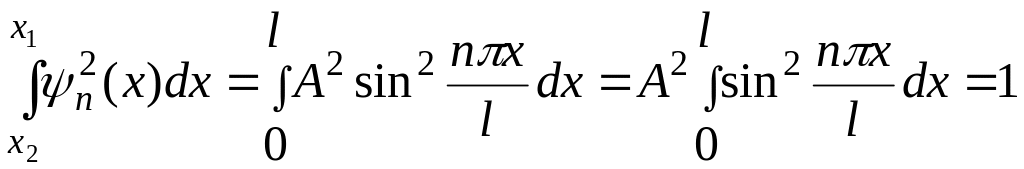На концах интервала ( 0, l ) подынтегральная функция равна нулю, поэтому значение интеграла можно представить как произведение среднего значения квадрата синуса на ширину ямы.
,
откуда
Т.е. собственные функции в данном случае имеют вид
n
=
1, 2, 3…