Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

«ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к решению задач по атомной физике

для студентов физического факультета

Ростов-на-Дону

2006

Методические указания разработаны кандидатом физико-математических наук, ассистентом кафедры нанотехнологии И.Н. Леонтьевым и кандидатом физико-математических наук, зав. кафедрой нанотехнологии Ю.И. Юзюком.

Ответственный редактор канд. физ.-мат. наук И.Н. Леонтьев

Компьютерный набор и верстка инженер Г.А. Колесников

Печатается в соответствии с решением кафедры общей физики физического факультета РГУ, протокол № 21 от 25 апреля 2006 г.

Основные формулы

• Формула де Бройля, выражающая связь длины волны  с импульсом p движущейся частицы:

а) в классическом приближении ( , )

;

б) в релятивистском случае (скорость v частицы сравнима со скоростью света с в вакууме )

.

• Связь длины волны де Бройля с кинетической энергией К частицы:

а) в классическом приближении ;

б) в релятивистском случае , где Е₀ – энергия покоя частицы ( ).

• Соотношение неопределенностей Гейзенберга:

а) для координаты и импульса частицы , где p_x – неопределенность проекции импульса частицы на ось х, х – неопределенность ее координаты;

б) для энергии и времени , где Е – неопределенность энергии данного квантового состояния, t – время пребывания системы в этом состоянии.

• В одномерном случае временное и стационарное уравнение Шредингера будут иметь вид

, ,

где i – мнимая единица, m – масса частицы; – волновая функция, описывающая одномерное движение свободной частицы, А – амплитуда волны де Бройля, p – импульс частицы, Е – полная энергия частицы, U(x) – потенциальная энергия, ψ(х) – координатная часть волновой функции.

• Для случая трех измерений временное и стационарное уравнение Шредингера записывается в виде

, ,

где – оператор Лапласа.

При решении уравнения Шредингера следует иметь в виду стандартные условия, которым должна удовлетворять волновая функция: конечность (во всем пространстве), однозначность, непрерывность самой Ψ – функции и ее производной.

• Вероятность P обнаружить частицу (в одномерном случае) в интервале от х₁ до х₂

.

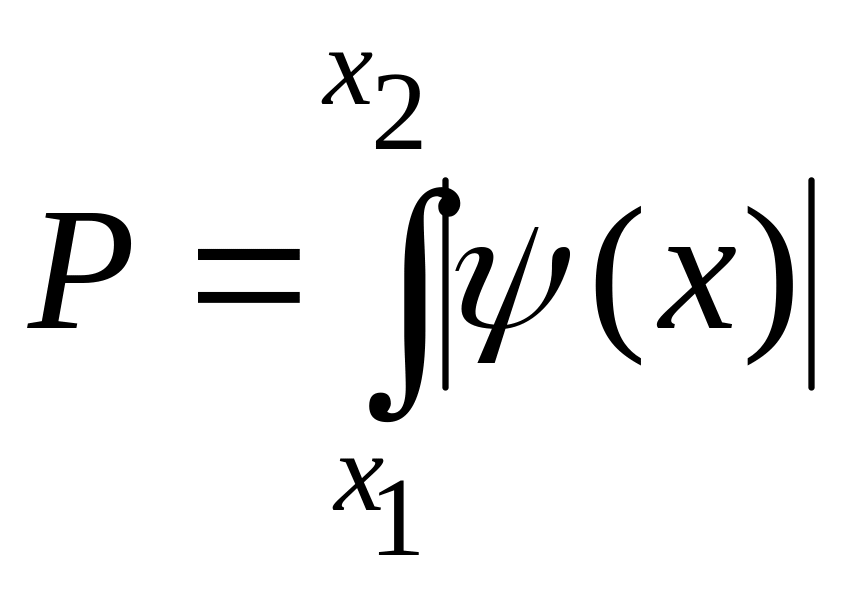
• Коэффициент прозрачности D потенциального барьера U(x):

,

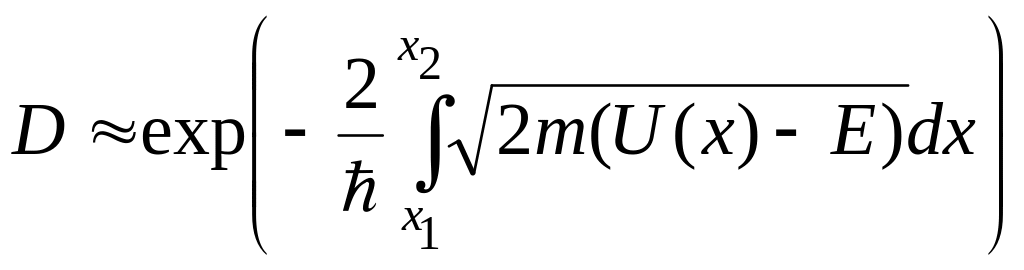где х₁ и х₂ – координаты точек, между которыми U > E.

Задача №1

Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля  для двух случаев: 1) U₁ = 51 В; 1) U₂ = 510 кВ.

Длина волны де Бройля частицы зависит от ее импульса и определяется формулой

. (1)

Связь импульса p с кинетической энергией К частицы для нерелятивистского (когда К<<mc²) и для релятивистского (когда К~mc²)случаев, выражается формулами:

, (2)

. (3)

Тогда (1) с учетом (2) и (3) в нерелятивистском и релятивистском случае примет вид

, (4)

. (5)

Чтобы решить какую из формул (4) или (5), следует применить для вычисления дебройлевской длины волны, сравним кинетическую энергию электрона, прошедшего заданные в условии разности потенциалов, с энергией покоя электрона.

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется выражением

.

В первом случае К₁ = eU₁ =51 эВ, что много меньше энергии покоя электрона m_ec² = 0,51 МэВ. Следовательно применяем формулу (4). Подставляя численные значения, получим ₁ = 172 пм.

Во втором случае К₂ = eU₂ = 510 кэВ, т.е. равна энергии покоя электрона. Следовательно, необходимо применить формулу (5). Произведя вычисления, получим ₂ = 1,4 пм.

Задача №2

Поток моноэнергетических электронов падает нормально на диафрагму с узкой щелью шириной b =2,0мкм. Найти скорость электронов, если на экране, отстоящем от щели на l = 50 см, ширина дифракционного максимума x = 0,36 мм.

При дифракции на одной щели условие первого дифракционного максимума имеет вид

, (6)

где b – ширина щели. Поскольку угол дифракции  достаточно мал, то

. (7)

Подставляя (7) в (6), получаем

. (8)

Дебройлевская длина волны электронов , падающих на щель, равна

. (9)

Подставляя (9) в (8), получим

.

Отсюда

= 0,96·10⁶ м/c.

Задача №3

Найти кинетическую энергию, при которой дебройлевская длина волны электрона равна его комптоновской длине волны.

Исходя из равенства ,

где – дебройлевская длина волны электрона,

– комптоновская длина волны электрона;

получаем

. (10)

Из релятивистской механики известно, что

, (11)

где К – кинетическая энергия частицы. Подставляя (11) в (10) получим

,

.

Решая это квадратное уравнение, получим

.

Поскольку кинетическая энергия не может быть отрицательной величиной, то

.

Задача №4

Пучок электронов с кинетической энергией К=10 кэВ проходит через тонкую поликристаллическую фольгу и образует систему дифракционных колец на экране, отстоящем от фольги на l= 10,0 см. Найти межплоскостное расстояние, для которого максимум отражения третьего порядка соответствует кольцу с радиусом r=1,6 см.

Для решения данной задачи воспользуемся законом Вульфа-Брэгга

,

где d – межплоскостное расстояние,  – угол дифракции, n – порядок дифракционного максимума, – дебройлевская длина волны электронов, имеющих кинетическую энергию К. Тогда

.

Отсюда

.

Поскольку

.

То

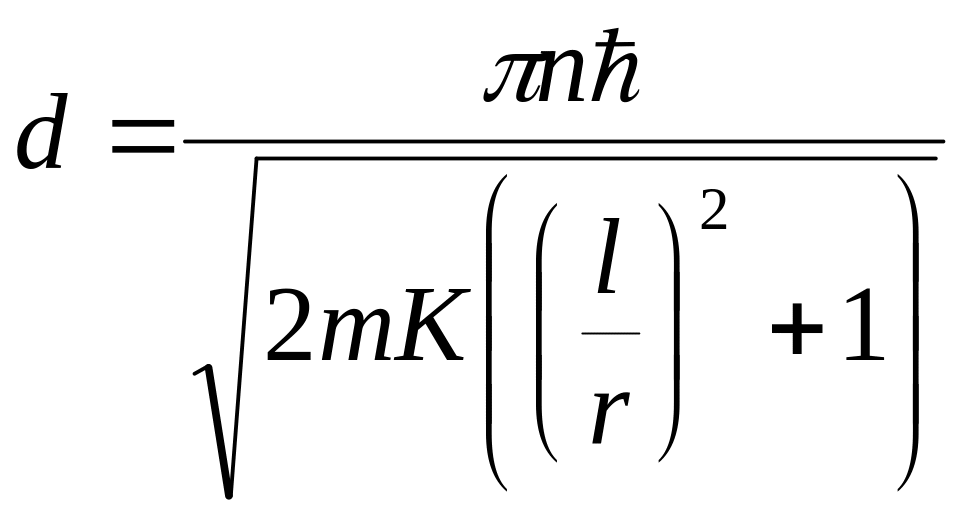= 0,23 нм.