Конфігурація зовнішніх планет:

1 — сполучення;

2 — протистояння;

3 — західна квадратура;

4 — східна квадратура.

Отже, конфігураціями зовнішніх планет є сполучення, протистояння, західна та східна квадратури.

Моменти конфігурацій планет і умови їх видимості на кожен рік друкують в астрономічних календарях.

Рух планет Сонячної системи не є безладним та невпорядкованим. Вони обертаються навколо Сонця згідно із законами, які на початку XVII століття відкрив видатний німецький учений Й.Кеплер (1571-1630).

Щоб зрозуміти суть першого закону Кеплера, зробимо короткий екскурс у геометрію.

Еліпсом називається плоска замкнена крива, що складається з точок, сума відстаней від яких до двох даних точок F₁ та F₂ є величиною сталою (див. рис.). Точки F₁ та F₂ називаються фокусами еліпса. Середина відрізка F₁F₂ точка О —: ц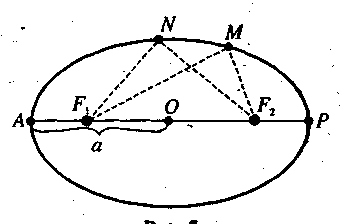 ентр еліпса. Відрізок АР = 2а — називається великою віссю, а відрізки АО та ОР — великими півосями еліпса

(АО = ОР = а).

Якщо М та N — довільні точки еліпса, то за означенням:

МF₁ + МF₂ = NF₁ + NF₂ = АF₁ + АF₂ = 2а.

Відрізок, що з'єднує довільну точку еліпса з одним з його фокусів (наприклад, МF₁), називається радіус-вектором цієї точки. Відношення називається ексцентриситетом еліпса і характеризує його витягнутість. Що більше витягнутий еліпс, то більший його ексцентриситет, проте у будь якому випадку 0 ≤ e < 1.

Якщо e = 0, тобто ОF₁ = 0 (фокуси еліпса збігаються з його центром), то еліпс перетворюється в коло.

Еліпс має чимало цікавих властивостей, однією з яких є оптична: світлові промені, які виходять з одного фокуса, після дзеркального відбивання від еліпса проходять через інший фокус.

Перший закон Кеплера.

Орбіти планет є еліпсами зі спільним фокусом, у якому міститься Сонце.

Р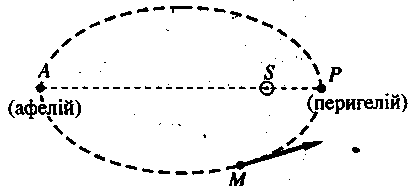 ухаючись навколо Сонця S (див. рис.), планета М періодично віддаляється та наближається до нього, тобто відстань між ними постійно змінюється.

Афелієм називається найдальша від Сонця точка траєкторії планети (точка А), а перигелієм найближча (точка Р).

Середньою відстанню від Сонця до планети вважають середнє арифметичне її афелійної та перигелійної відстаней. Ця відстань дорівнює великій півосі орбіти планети: .

Лінія АР називається лінією апсид.

Велика піввісь земної орбіти a_⊕ — одна астрономічна одиниця

(1 а.о.) — прийнята за одиницю довжини в астрономії,

a_⊕ = 1 а.о. = 1,4959787 ∙ 10¹¹ м ≈ 150 000 000 км.

У перигелії (3 січня) відстань між Землею і Сонцем на 2,5 млн. км менша, а в афелії (3 липня) — на стільки ж більша за астрономічну одиницю.

Ексцентриситети орбіт планет Сонячної системи малі, тобто траєкторії дуже близькі до колових. Найбільш вигнутими є орбіти Плутона (е = 0,247) та Меркурія (е = 0,207). Ексцентриситет земної орбіти е_⊕ = 0,017 .

Другий закон Кеплера.

Радіус-вектор планети за однакові проміжки часу описує рівні площі.

Другий закон Кеплера формулюють іноді так: секторна швидкість планети — величина стала. Це означає: якщо за однакові проміжки часу планета проходить дуги К₁К₂ та Т₁Т₂ , то площі секторів SК₁К₂ та SТ₁Т₂ рівні (див. рис.).

З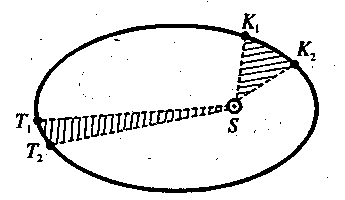 гідно із другим законом Кеплера, лінійна швидкість планети неоднакова у різних точках орбіти. Швидкість планети відносно Сонця поблизу перигелія найбільша, а поблизу афелія — найменша. Наприклад, Марс поблизу перигелія рухається зі швидкістю 26,5 км/с, а біля афелія сповільнюється до 22 км/с.

Комети, як і планети, рухаються навколо Сонця за тими ж законами, проте їхні орбіти дуже витягнуті (ексцентриситети орбіт великі). Тому поблизу Сонця (в перигелії) швидкість деяких комет досягає значення 500 км/с, а в афелії вони рухаються дуже повільно.

Третій закон Кеплера.

Квадрати зоряних (сидеричних) періодів обертання планет відносяться як куби великих півосей орбіт.

Якщо Т₁ та Т₂ — сидеричні періоди обертання планет, а а₁ та а₂ — середні відстані від планет до Сонця (великі півосі їхніх орбіт), то третій закон можна записати так: .

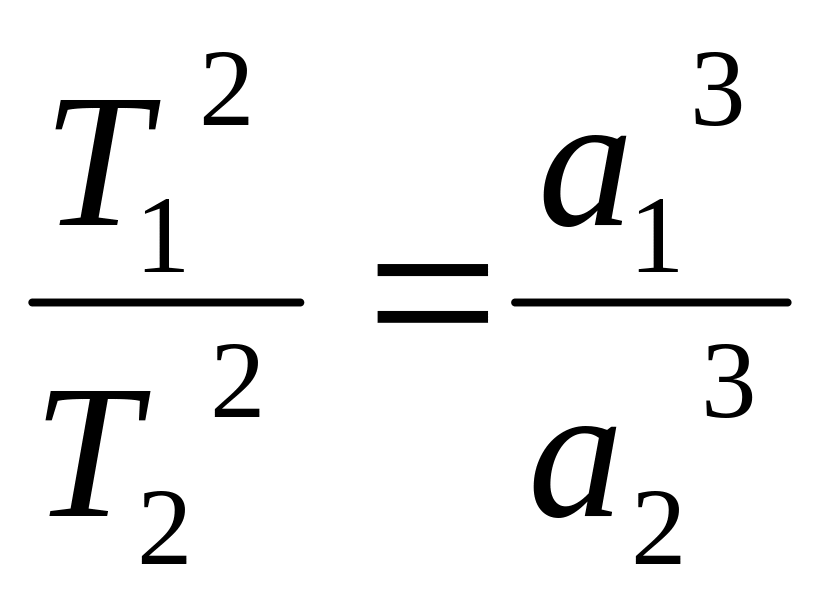Записавши третій закон Кеплера для Землі та іншої планети, маємо:

, або Т² = а³ , де Т — в роках, а — в а.о.

Тобто квадрат сидеричного періоду планети, вираженого в земних (сидеричних) роках, дорівнює кубу великої півосі її орбіти, вираженої в астрономічних одиницях.

Відкриття третього закону Кеплера дозволило обчислити відстані від Сонця до планет, періоди обертання яких вже були відомі.

Поряд із розглянутим способом визначення відстаней у Сонячній системі існують й інші. Найвідомішим є тригонометричний метод, який дозволяє знаходити відстані до недоступних предметів, використовуючи явище паралактичного зміщення.

Паралактичним зміщенням називається зміна напрямку на об'єкт при переміщенні спостерігача.

Н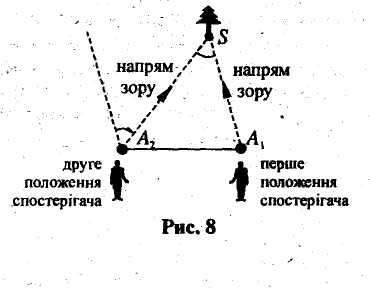 ехай спочатку предмет S розглядають із точки A₁ (див. рис.). Після переміщення спостерігача у точку А₂ йому, щоб бачити предмет, необхідно змінити напрям зору на певний кут. Очевидно, що з віддаленням предмета S , цей кут зменшуватиметься. Тому щоб помітити паралактичне зміщення далеких предметів, необхідно, щоб базис А₁А₂ (відстань між точками спостереження) був значним.

Зокрема при спостереженнях об'єктів Сонячної системи фазисом є радіус Землі, а при спостереженні зір та галактик — велика піввісь земної орбіти.

Горизонтальним паралаксом (від грецького parallaxis — відхилення, зміщення) називається кут р, під яким зі світила видно радіус Землі, перпендикулярний до напрямку зору.

Використовуючи обертання Землі навколо своєї осі (див. рис.), спочатку спостерігаємо світило S на горизонті з точки A₁ , а через деякий час — у зеніті — і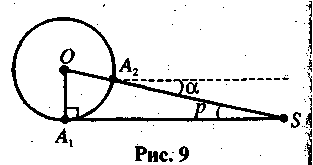 з точки А₂. Зрозуміло, що напрям на світило при цьому змінюється щ кут α , який дорівнює горизонтальному паралаксу світила: α = р.

Відстань, до світила SO можна визначити з

, ,

де ≈ 6370 км — радіус Землі, p — паралакс світила.

Відстані між об'єктами Сонячної системи значні, і хоча базисом спостережень є радіус Землі, паралакси планет, супутників та Сонця дуже малі. Наприклад, паралакс Сонця p_⊙ = 8,8' , а паралакс Місяця p_ε = 57'. Для малих кутів (у радіанах) справедливе співвідношення sin р ≈ р .

Тоді відстань до світила: .

Задача. Визначити відстань від Землі до Урану, якщо його горизонтальний паралакс дорівнює 2,21 ∙ 10^-6 радіан.