2.4. Раціональний вибір і поведінка децидента

Зазвичай у разі використання функцій корисності виникає таке природне запитання: чи не можна децидента замінити автоматом і чи зберігаються при цьому хоч якісь особ­ливості поведінки децидента? Для відповіді на нього різні дослідники моделювали мо­жливі ситуації та відповіді децидента, що дало змогу виявити відхилення, що виника­ють. Ці відхилення, зумовлені як властивостями суб'єкта, який приймає рішення, так і способом формулювання запитань, відображають відповідні парадокси.

Парадокс Аллє

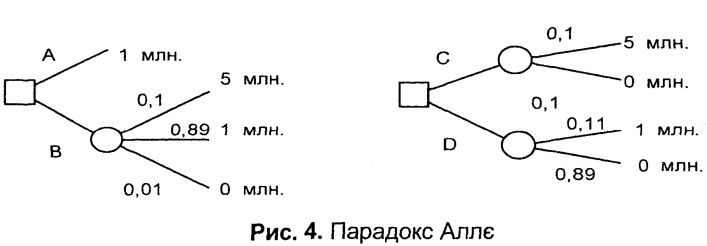
Французький учений Аллє запропонував розглянути дві лотереї (рис. 4). На рис.4, α децидент може обрати одну альтернативу з двох: отримати 1 млн (альтер­натива А) чи згодитися на лотерею, у якій імовірність виграшу 5 млн становить 0,10, 1 млн - 0,89, а ймовірність не виграти нічого - 0,01 (альтернатива В). Переважна більшість людей обере альтернативу А, хоча середній виграш для альтернативи В біль­ший. Оскільки максимально можливий виграш становить 5 млн, а мінімальний - 0, то U(5) = 1 і U(0) = 0, а невідоме значення корисності U( 1) = U. Оскільки у цьому випадку переважна більшість віддасть перевагу альтернативі А, то U > 0,1 × 1 + 0,89 × U, тобто U > 10/11.

У лотереї ж, проілюстрованій на рис. 4, б, більшість людей віддадуть перевагу аль­тернативі С перед альтернативою Д і тоді 0,10 × 1 > 0,11 × U, тобто U < 10/11. Отже, роблячи такий вибір, люди не діють згідно з функцією корисності.

Наведемо ще один приклад, який засвідчує нетривіальність процесу одержання ко­рисності та її залежність від схильності децидента до ризику. Розглянемо дві лотереї, характеристики яких наведено на рис 5.

За допомогою безпосереднього обчислення можна впевнитися, що середня ціна цих лотерей однакова. Проте це ще не означає, що децидентові байдуже, яку лотерею об­рати. Результати опитування показали, що найчастіше обирають другу лотерею, у якій ризик програшу відсутній. Зрозуміло, що у багатьох випадках значення ймовір­ностей не є наслідком тривалих спостережень і нагромадження статистичних даних, а результатом опитування експертів. Проте і в цьому випадку теорія суб'єктивної очі­куваної корисності, побудована на суб'єктивних імовірностях, має формальне обґрун­тування, але питання про причини парадоксальної поведінки децидентів у задачах прийняття рішень, пов'язаних з деревами рішень і максимізацією очікуваної суб'єк­тивної корисності, залишають відкритими.

Нераціональна поведінка децидентів і її причини

Визначення корисності по суті є суб'єктивним. Воно залежить від ставлення дециден­та до ризику. Нехай існують дві рівноймовірні можливості того що інвестиція в 100 000 грн принесе прибуток у 200 000 грн або ж буде марною (дасть прибуток 0 грн). Відповідне значення очікуваного прибутку становить 200 000×0,5 - 100000×0,5 = 50 000 грн. Хоча в цьому разі очікується прибуток, різні особи можуть інтерпретувати його неоднаково. Один інвестор, який ризикує, може вкласти гроші, щоб з імовірністю 0,5 отримати прибуток в 200 000 грн, а інший, обе­режніший, не виявить бажання ризикувати 100 000 грн, тобто різні дециденти неод­наково ставляться до ризику в ідентичних ситуаціях.

Розглянемо цю ситуацію з погляду корисності. Найкраща виплата становить 200 000 грн, а найгірша - (-100 000) грн. Отже, корисність у шкалі від 1 до 0 має значення 1 для 200 000 грн, та 0 для (-100 000) грн. Інакше кажучи, U( —100 000) = 0, a U(200 000) = 1, тому корисність задано в інтервалі від -100 000 до 200 000 грн.

Якщо особа байдужа до ризику, то функція корисності є прямою, що з'єднує точки (0, -100 000) та (1, 200000) (рис. 6, пряма b).

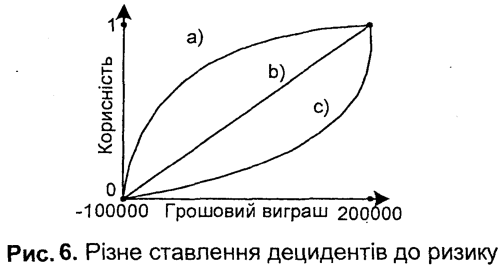
Крива a відображає функцію корисності децидента, не схильного до ризику оскільки виявляє більшу чутливість до втрат, а не до виграшів. Натомість децидент, поведінці якого відповідає крива с, налаштований на ризик.

Наявність систематичних відхилень від раціональної поведінки потребувала додатко­вих досліджень, результати яких дістали відображення насамперед у працях психоло­гів, зокрема Д. Канемана, А. Тверського, П. Словіка, в 70-х роках минулого сторіччя.

Один з найвідоміших прикладів нераціональної поведінки особи - «дилема генера­ла», суть якої є наступною. Генерал програв війну та хоче вивести своє військо (600 осіб) із території противника. Він може зробити це однією з двох доріг, і попередня розвідка дала інформацію про очікувані втрати в разі обрання зазначених маршрутів. Можливості виведення війська проілюстровано на рис. 7, на якому їх подано в екві­валентних із погляду корисності варіантах лотерей а (у вигляді виграшів) і b (у ви­гляді втрат).

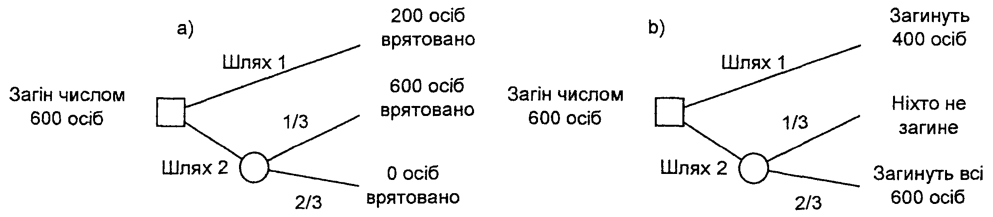
Рис. 7. Дилема генерала

У випадку, коли для оцінювання пред'явлено рис. 7.7, a, більшість осіб обирають шлях 1, уникаючи лотереї, у якій можуть загинути всі. Якщо для оцінювання взяти рис. 7, б, то більшість оберуть шлях 2, де з імовірністю 1/3 можна зберегти весь осо­бовий склад.

На основі багатьох експериментів було визначено основні евристики, які допомага­ють зрозуміти причини відхилень осіб від раціональної поведінки.

Твердження за представництвом. У багатьох випадках дециденти стверджують про належність певного об'єкта О до класу К лише за подібністю О до представницького об'єкта ОК класу К та майже не беруть до уваги апріорні ймовірності, що впливають на цю належність.

Твердження за кількістю подій. У багатьох ситуаціях дециденти оцінюють імовірно­сті подій на основі власного досвіду, виходячи з того, як часто вони зустрічалися з такими подіями та наскільки важливими вони були для них.

Твердження за точкою відліку. Якщо для оцінювання ймовірностей як точку відліку використовують початкову інформацію, то вона суттєво впливає на результат.

Наддовіра. Дециденти мають тенденцію надмірно довіряти власним твердженням, особливо тоді, коли вони стосуються минулих подій.

Прагнення до уникнення ризику. В реальних ситуаціях прийняття рішень дециденти прагнуть виключити варіанти, пов'язані з ризиком, і згоджуються на еквівалентні або дещо гірші варіанти,'в яких навіть з дуже малими значеннями ймовірностей можливі втрати.

Вивчення цих евристик дозволило сформулювати основні причини нераціональності поведінки осіб-децидентів, які наведені нижче:

• недостатня інформованість децидента в процесі вибору рішення;

• недосвідченість децидента, який навчається, а тому змінює свої переваги;

• прагнення децидента знайти рішення, оптимальне за декількома критеріями, які впорядковано за важливістю, і неспроможність зробити це.

• відмінність між часом, об'єктивно потрібним для реалізації, і тим, який запланував децидент.

В економічних дослідженнях розрізняються переваги, що спостерігаються, та виявле­ні переваги. Це зумовлено розв'язанням однієї з найважливіших задач передбачення поведінки споживача стосовно певних груп послуг і товарів, що дає змогу визначити попит, оцінити обсяг випуску та ціну певного товару чи послуги. У цій ситуації важ­ливо визначити, чи слід брати до уваги в задачах економічного вибору нераціональ­ність поведінки осіб.

Переваги, що спостерігаються, визначають, вивчаючи дані про купівлі та продажі, що дозволяє будувати відповідні математичні моделі, які описують попит споживачів на певні товари та послуги, і передбачити поведінку споживачів стосовно певного чи близького до нього товару (послуги).

Однак знання поведінки й евристик не надає нової інформації для визначення пере­ваг, що спостерігаються, тому що відповідні моделі є дескриптивними. Якщо поведін­ка відрізнятиметься від раціональної, то прогностичні здатності моделі не зміняться, і вона описуватиме таку поведінку, яка спостерігається. Якщо, наприклад, відомо, що окремий споживач вибрав сорт чаю нераціонально, залежність попиту на чай від його ціни визначатимуть для групи споживачів загалом, не беручи до уваги, наскільки люди діють раціонально, купуючи чай.

Натомість у разі виявлених переваг потрібно спрогнозувати попит, ґрунтуючись на опитуваннях споживачів іще до їх вибору. У цьому випадку результати психологіч­них досліджень будуть важливими й опитування провадяться з урахуванням особо­вих евристик, що дає змогу підвищити надійність таких опитувань. Існує твердження, що ринок привчає до раціональності, і значні відхилення від неї можуть розорити де­цидента, однак важко визначити, наскільки корисним є такий досвід.

Теорія проспектів

Прагнення врахувати евристики нераціональної поведінки, реальну поведінку осіб зумовило розроблення А. Тверським та Д. Канеманом теорії проспектів. Її призначен­ням є урахування реальних рис поведінки людей у завданнях прийняття рішень із суб'єктивними оцінками ймовірності як альтернативи теорії очікуваної корисності. Теорія проспектів побудована з урахуванням таких ефектів поведінки людини:

• відбиття, тобто зміни переваг у разі переходу від виграшів до втрат;

• визначеності, що виявляється як тенденція надання більшої ваги детермінованим реалізаціям;

• ізоляції, тобто тенденцію до спрощення вибору за допомогою виключення спіль­них компонент варіантів рішень.

Розглянемо гру (рис. 8), у якій альтернатива х реалізується з імовірністю р, альтер­натива у - з імовірністю q, а нульова альтернатива - з імовірністю 1 -p-q. Таку гру в теорії проспектів називають проспектом.

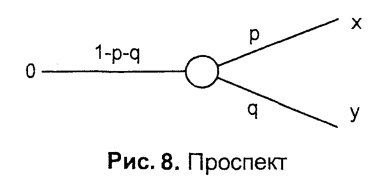
Цінність (це не те ж саме, що очікувана корисність) такої гри визначають наступним чином:

V= V(x) × W(p) + V(y) × W(q)

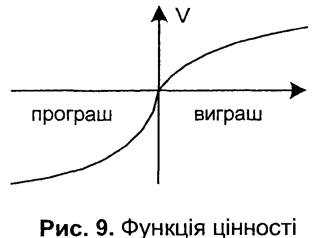
де V(x), V(y) - відповідно цінності альтернатив х та y, V(0) = 0, W(p), W(q) - вага (важливість) імовірностей р та q. У функції цінності, на відміну від функції корисно­сті, замість імовірностей використовуються функції від імовірностей. Цінність відра­ховують від довільного рівня, який уважають початковим. Щоб узяти до уваги аспек­ти, пов'язані з особливостями поведінки, припускають, що функція цінності опукла для виграшів і ввігнута - для програшів, і її нахил для втрат більший, аніж для ви­грашів (рис. 9).

Важливою відмінністю теорії проспектів від теорії очікуваної корисності є спосіб ура­хування ймовірностей. У теорії очікуваної корисності розглядають безпосередньо імо­вірності, а в теорії проспектів - використовують функцію ймовірності, яка надає різ­ним значенням імовірностей різної ваги. Загалом ця функція має вигляд, наведений на рис. 10. Її використовують для відображення аспектів поведінки децидентів.

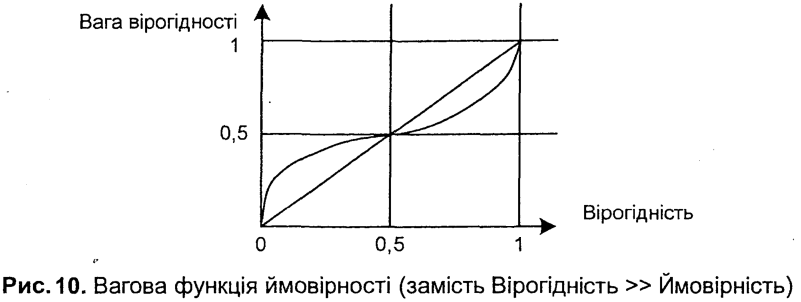
Унаслідок зважування не виконуються закони теорії ймовірностей, однак вагова функ­ція має такі властивості:

• W(0) = 0, W( 1) = 1;

• W(p) + W(1 -ð) < 1;

• для малих значень імовірностей W(p) > р;

• відношення W(p)/W(q) ближче до 1 за малих значень імовірності, аніж за великих;

• функція W(p) погано визначена поблизу граничних значень.

Для виконання вибору між різними варіантами альтернатив теорія проспектів реко­мендує наступну послідовність дій.

1) Редагування проспекту, визначеного достатньо неформально. Воно складається з та­ких дій.

• Обрання опорної точки.

• Об'єднання однакових результатів з обчисленням суми їх імовірностей.

• Видалення еквівалентних альтернатив з однаковими ймовірностями.

• Видалення домінованих альтернатив.

• Заокруглення значень цінностей і ймовірностей.

2) Обчислення значень цінності для різних альтернатив і вибір варіанту з найбіль­шим значенням цінності.

Теорія проспектів дає змогу уникнути деяких парадоксів (наприклад, парадокса Аллє), але не розв'язує всіх суперечностей між нормативною теорією, що диктує норми раціональної поведінки, й особливостями поведінки реальних осіб. Це пояснюється недостатньо формалізованою процедурою редагування проспекту, у якій дозволяєть­ся використовувати суперечливі евристики.

Однак, незважаючи на можливі суперечності, теорія проспектів допомагає одержати чи­мало практично корисних результатів. Це аксіоматична теорія, що об'єднує дескриптивні знання про поведінку децидентів із нормативними правилами раціональної поведінки.