2.3. Умови існування функції корисності Криві байдужості та функції корисності

Децидент може структурувати свої переваги, будуючи криві байдужості. Якщо цін­ність залежить 'від двох координат, то її можна відобразити у двовимірному просторі. Якщо альтернатива А, що відповідає точці х⁽¹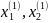⁾ = ( ) (рис.3) із погляду децидента еквівалентна альтернативі В, яка відповідає точці х⁽²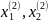⁾ =( ) , то ці дві точки належать одній і тій же кривій байдужості, а якщо альтернатива С, яка дає точці х⁽³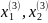⁾ = ( ) , ліпша за попередні, то вона, належить іншій кривій байду­жості (рис. 7.3). В n-вймірному просторі через будь-яку точку проходить гіперповерхня байдужості, до якої належать усі точки однаковою корисністю.

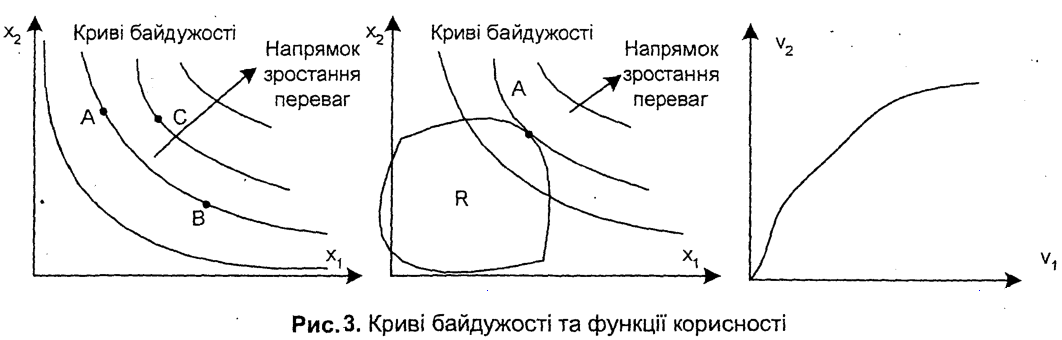
Між побудовою структури переваг децидента та пошуком відповідної функції корис­ності існує тісний зв'язок. Врешті-решт, можна використовувати різні функції корис­ності, щоб децидент міг чіткіше висловлювати свої переваги.

Деякими видами функцій корисності для двовимірного простору, що застосовуються на практиці, є наступні: лінійна, функція Коба - Даґласа та їх комбінація:

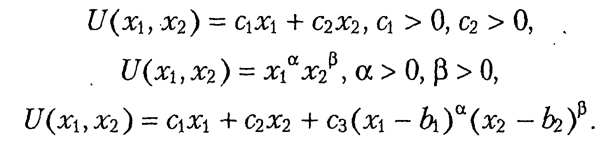
Якщо задано функцію корисності, то будь-які дві точки з рівними між собою значен­нями корисностей є нерозрізняльні за перевагою та знаходяться на одній кривій бай­дужості.

Ральф Кіні та Ґовард Райфа ввели поняття стратегічно еквівалентних функцій корисності. Дві функції корисності стратегічно еквівалентні, якщо вони мають одні й ті самі криві байдужості та зумовлюють одне й те саме лінійне впорядкування за пере­вагою для довільних альтернатив, що належать до множини допустимих.

Бінарні відношення та функція корисності

Припустімо (не конкретизуючи властивостей), що систему переваг децидента відоб­ражає бінарне відношення « ». Функція корисності f: A→R, пов'язана з бінарним відношенням є наступною:

де A - множина допустимих альтернатив, R - множина дійсних чисел, f(a) - значен­ня функції корисності для альтернативи а. Таким чином, якщо альтернатива а краща за альтернативу b, то й її корисність має бути більшою для всіх альтернатив, що нале­жать допустимій множині. Звичайно ж, не для всіх бінарних відношень існує функція корисності, тому потрібно дослідити, за яких умов це можливо.

Це завдання є предметом вивчення математичної теорії корисності. Уперше питання про можливість подання відношення переваги за допомогою функції корисності роз­глянув Г. Кантор (1895 p.). Відношення переваги обов'язково асиметричне, однак для його продуктивного використання потрібно визначити ще й додаткові умови. Це було предметом дискусій у минулому, та й тепер цю проблему продовжують обговорюва­ти. Такі додаткові умови формулюють зазвичай у вигляді аксіом, певних гіпотез про закономірності процесу вибору, і обґрунтованість деяких припущень є предметом дискусій.

Окрім того, деякі аксіоми, логічні у випадку окремого розгляду, виявляються супер­ечливими при побудові системи аксіом Таким чином, слід визначити, мінімальні комбінації аксіом, які не суперечать одна одній і да­ють можливість побудувати набір припущень про закономірності вибору, який можна використати конструктивно.

Можливість побудови функції корисності для бінарного відношення й обґрунтовує такий набір аксіом, який називають аксіомами корисності.

Аксіома 7.1. Якщо - асиметричне відношення переваги, ≈ - відношення нерозріз- няльності (толерантності), то для будь-яких довільних альтернатив a, b є А справед­ливе одне з трьох співвідношень a b, b а, а ≈ b.

Якщо ж виконується співвідношення (a, b ϵ A): a ≈b ↔ (¬(a b)) ᴧ (¬(b а)), то ак­сіома 7.1 завжди справджується.

Аксіома 7.2. Виконується умова (a ϵ А): а ≈ а, тобто будь-яка альтернатива нерозрізняльна сама із собою (це наслідок означення відношення тoлерантності).

Аксіома 7.3. Виконується умова (a, b, с ϵ А: ((а ≈ b) ᴧ (b ≈ c)) → (а ≈ с), тобто умо­ва транзитивності відношення толерантності.

Ця аксіома не очевидна, існують приклади та достатньо логічні ситуації, в яких вона не діє. Як приклад можна розглянути парадокс купи. Якщо додавати послідовно по одній піщинці, то врешті-решт утвориться купа піску. Однак на початковій стадії ку­пи немає, і два послідовні етапи цього процесу нерозрізняльні.

Аксіома 7.4. Виконується умова (a, b, с ϵ А): ((а b) ᴧ (b с)) → (а с), тобто від­ношення переваги транзитивне.

Аксіома 7.5. Виконується умова (a, b, с ϵ А): ((a b ) ᴧ (b ≈ с)) → (а с), тобто коли альтернатива а ліпша за b, а b нерозрізняльна з с, то альтернатива а краща за с_. Ця аксіома є припущенням про те, що децидент має доволі глибоку розрізняльну здатність, тобто може розрізнити дві доволі близькі між собою альтернативи.- .

Аксіома 7.6. Виконується умова (а, b, с ϵ А): ((а ≈ b) ᴧ (b с)) → (а с), аналогічна аксіомі 7.5. ,

За допомогою цих припущень можна задати функцію корисності f для якої викону­ються умови (7.4).

Функції корисності, задані з точністю до лінійного перетворення

Наведених вище аксіом недостатньо для того, щоб однозначно визначити вигляд фу­нкції корисності. Справді, у разі скінченної кількості альтернатив нестроге впорядку­вання дає змогу лише впорядкувати їх від найгіршої до найліпшої (чи у зворотному порядку). Цій послідовності можна поставити у відповідність довільну послідовність чисел, що зростають (для зворотного порядку - що спадають). Одержану послідов­ність можна розглядати як значення певної функції корисності, тобто виявляється, що функцію корисності задано з точністю до монотонного перетворення.

Щоб перейти від відношення переваги до функції корисності, заданої з точністю до лі­нійного перетворення, потрібно ввести додаткові аксіоми комбінування, які визначають модель поведінки децидента у випадку невизначеності дії.

Нехай а та b - довільні альтернативи, a, b ϵ А, та 0 < r < 1, 0 < s < 1. Тоді альтерна­тива r×a+(1-r)×b є комбінацією альтернатив, котру можна розглядати як лоте­рею, у якій реалізуються два можливі результати - а з імовірністю rib з імовірністю (1-r). Припустімо, що для цієї лотереї виконуються наступні аксіоми.

Аксіома 7.7. Для будь-якої лотереї 0 < r < 1 на a, bϵ А виконується умова r×а + (1 - r) × b = (1 - r) × b + r × а.

Ця властивість називається комутативністю лотереї, вона має технічне значення та, по суті не обмежує переваг децидента.

Аксіома 7.8. Для будь-яких лотерей 0 < r < 1, 0 < s < 1 на a, b, с ϵ А виконується умова

r × а + (1 - r) × (s × b + (1 - s) × с) = r × а + (1 - r) × s × b + (1 - r) × (1 - s) × с. Ця властивість відповідає припущенню про те, що порядок лотерей неважливий для де­цидента.

Аксіома 7.9. Для будь-яких 0<r<1, аϵА справедливе співвідношення r × а + (1 - r) × а = а, тобто лотерея є рефлексивною.

Аксіома 7.10. Якщо а ≈ с, то для будь-яких b, r (a, b, с ϵ А, 0 < r < 1) виконується умова (г × а + (1 - r) × b) ≈ (r × с + (1 - r) ×b).

Аксіома 7.11. Якщо а с, то для будь-яких b, r (a, b, с ϵ А, 0 < r < 1) виконується умова (r × а + (1 - r) × b) (r × с + (1 - r) × b).

Аксіома 7.12. Нехай a c b, a, b, с ϵ А. Тоді існує таке 0 ≤ r ≤ 1, що виконується умова (r × а + (1 - r) × b) ≈ с. Ця аксіома є важливою і має окрему назву - аксіома неперервності.

Наведені аксіоми дають можливість сформулювати й довести фундаментальний ре­зультат, отриманий Дж. фон Нойманом і О. Моргенштерном.

Теорема 7.1 (Ноймана - Моргенштерна). Якщо для відношення переваги викону­ються аксіоми 1-12, то існує функція f: А → R, така, що для довільних a, b ϵ А та будь-якого r ϵ [0, 1], для якої виконуються співвідношення

f(a)>f(b)↔a b,

f(r×a) + (1-r)×b) = r× f(a) + (1 - r) × f(b).

Ця функція визначена з точністю до позитивного лінійного перетворення, тобто якщо для функції F виконано умови (5), (6), то F(a) = α×f(a) +β , де α > 0 та β - кон­станти.

Доведення. Якщо для всіх альтернатив a, b ϵ А виконується а ≈ b, то можна вважати, що значення функції f всюди дорівнює константі, наприклад 0.

Вважатимемо, що існують альтернативи a, b ϵ А, такі, що а b. Тоді для довільної альтернативи с можливі п'ять умов:

1) c a;

2) c a;

3) a c b

4) c ≈b;

5) b c;

Позначимо а = е_1, b = е₀. Нехай f(e₁) = 1, f(е₀) = 0. Згідно з аксіомою неперервності у випадку 1 існує таке r, що r×c + (l-r)×b)≈a. Припустімо, що тоді f(с) = 1 /r. У випадку 2 нехай f(c) = 1, а у випадку 3 існує таке s, що s × а + (1 - s) × b = с. Тоді нехай f(c) = s. У випадку 4 візьмемо f(с) = 0, а у випадку 5 нехай існує таке t ϵ [0, 1], що t × с + (1 - t) × а =b. У цьому випадку покладемо f(с) = (t - 1 )/t.

Наступним кроком потрібно довести, що для так заданої функції виконується умова (4) для довільних альтернатив z₁ і z₂. Потрібно послідовно розглянути альтернативи z₁ і z₂, що задовольняють наведені вище п'ять умов у різних сполученнях. Доведемо один випадок, у якому для альтернатив z₁ і z₂ виконано умову 1 (інші 14 доводяться аналогічно, тому ми не будемо розглядати їх). Нехай f(z₁ )= s₁ та f(z₂) = s₂, s₁ s₂. До­ведемо, що z₁ z₂.

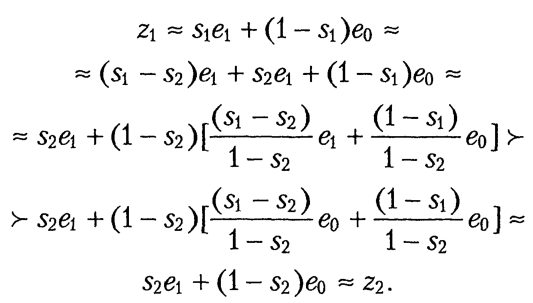
Виконавши ці перетворення в зворотному порядку, дійдемо висновку, що правильне й обернене твердження. Доведемо, що для заданої вище функції f справедливе спів­відношення (3). Відомо, що z₁ ≈ s₁ e₁ + (1 - s₁) e₀, z₂ ≈ s₂ e₁+ (1 - s₂)e₀. Отже, для до­вільного 0 < r < 1 виконується умова :

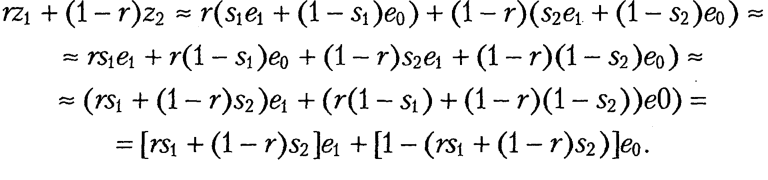
Позначимо γ = rs₁ + (1 - r)s₂. За побудовою функції f(.), f(γ e₁ + (1 - γ)е₀ + γ. Тому f(rz₁ + (1 - r)z₂) = rs₁ + (1 - r)s₂ = rf(z₁) + (1 - r) f (z₂). Нехай тепер деяка функція F задо­вольняє умови (2) та (3). Оскільки е₁ е₀, то F(e₁) > F(e₀). Уважатимемо, що α = F(e₁) - F(e₀) > 0, β = F(e₀). Нехай тепер e₁ z е₀. Якщо f(z) = s, то z ≈ s e₁ + (1 - s)e₀, тобто F(z) = F(se₁ + (1 - s)e₀) = sF(e₁) + (1 - s)F(e₀) = s(α + β) + (1 - s)β, і, таким чином F(z) = αs + β = α f (z) + β.

Отже, аксіом 1-12 достатньо, щоб за відношенням переваги побудувати функцію корисності, єдину з точністю до лінійного перетворення (перенесення початку координат і зміни масштабу), тобто описати корисність у вигляді F(x) = af(x) + β, де f(x) -відома функція, а констайти α >0 та β є невизначеними. У задачах математичної економіки та керування доволі рідко відношення переваги використовують безпосередньо. Функцію корисності будують майже емпірично, хоча для певних задач придатні певні функції (наприклад, функція Коба - Дагласа як виробнича функція). Проте, щоб функцію ко­рисності було використано коректно, для відношення переваги, яке вона відображає, мають виконуватися 12 наведених вище аксіом.