3.3. Багатокритерійна теорія корисності Порядок застосування й аксіоми maut

Основні результати теорії корисності отримали подальший розвиток у багатокритерійній теорії корисності - MAUT (Multi - Attribute Utility Theory). Цей науковий напрям має такі особливості:

• будується функція корисності, що має аксіоматичне обґрунтування;

• деякі умови, від яких залежить вигляд цієї функції, можуть бути перевірені у діа­лозі з децидентом;

• використання отриманих результатів для оцінювання заданих альтернатив.

Основними етапами MAUT є наступні.

1. Складання переліку критеріїв.

2. Побудова функцій корисності за кожним із критеріїв.

3. Перевірка певних умов, від яких залежить вигляд загальної функції корисності.

4. Побудова залежності між оцінками альтернатив за критеріями та загальною які­стю альтернативи (багатокритерійної функції корисності).

5. Оцінювання наявних альтернатив і обрання найкращої.

Подібно до класичної теорії корисності, MAUT має аксіоматичне обґрунтування. Це означає, що сформульовано деякі умови (аксіоми), які має задовольняти функція ко­рисності децидента. Якщо умови задовольняються, то доводять існування функції ко­рисності того чи іншого вигляду. У багатокритерійній теорії корисності ці умови мо­жна поділити на дві групи.

До першої групи - загальних аксіом, ідентичних використовуваним у теорії корисно­сті, належать такі.

1. Порівняльність. Між корисностями будь-яких альтернатив можна встановити такі відношення: або одна з них краща за іншу, або вони однакові.

2. Транзитивність. Із переваги альтернативи А за корисністю над альтернативою В та переваги альтернативи В за корисністю над С випливає перевага альтернативи А за корисністю над альтернативою С.

3. Для співвідношень між корисностями альтернатив А,В,С, що мають вигляд U(A) > U(B) > U(C), можна вказати такі числа α та β (0 < α < 1, 0 < β < 1), що ви­конуватимуться умови α U(A) + (1 - α)U(C) = U(B), (1- β) U(A) + βU(B) > U(B).

Аксіома 3 ґрунтується на припущенні, що функція корисності неперервна, і можна оперувати будь-якими малими частинами корисності альтернатив.

Друга група аксіом - аксіоми незалежності - специфічна для МАUТ. Вони дають змогу стверджувати, що деякі взаємні відношення між оцінками альтернатив за кри­теріями не залежать від значень за іншими критеріями. Наведемо декілька умов неза­лежності.

• Незалежність за різницею. Переваги між двома альтернативами, що відрізняють­ся лише оцінками за порядковою шкалою одного з критеріїв Q_1, не залежать від однакових (фіксованих) оцінок за іншими критеріями Q₂ ,..., Q_n . На перший по­гляд ця умова здається природною й очевидною. Але вона виконується не завжди. Так, обираючи автомобіль, за приблизно однакової ціни двох моделей децидент схильний віддати перевагу більшій за розміром машині. Проте його перевага змі­нюється на протилежну, коли він дізнається, що в цієї машини не гідравлічна, а механічна коробка передач, що ускладнює керування.

• Незалежність за корисністю. Критерій Q₁ називається незалежним за корисністю від критеріїв Q₂,..., Q_n, якщо порядок переваг лотерей, у яких змінюються лише рівні критерію Q₁, не залежить від фіксованих значень за іншими критеріями. У багатокритерійній теорії корисності лотереї використовують для побудови функ­цій корисності за окремими критеріями.

• Незалежність за перевагами. Ці умови є одними з найважливіших умов, що час­то використовуються. Два критерії Q₁ та Q₂ незалежні за перевагою від інших критеріїв Q₃, ..., Q_n , якщо переваги між альтернативами, що різняться лише зна­ченнями Q₁ та Q₂ не залежать від фіксованих значень за іншими критеріями.

Перші дві аксіоми незалежності стосуються незалежності одного критерію від інших, третя ж — незалежності пари критеріїв від інших.

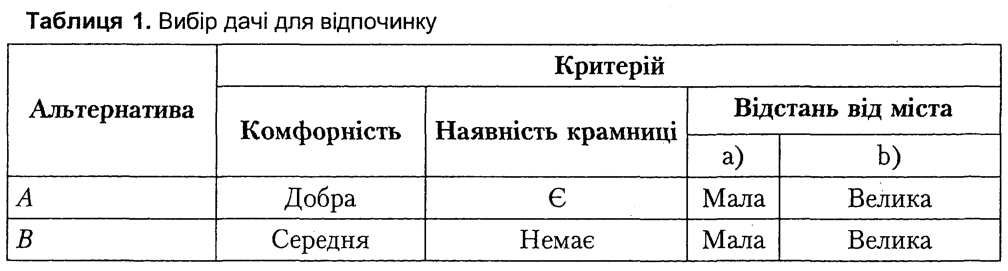
Хоча аксіому незалежності за перевагою широко використовують у МАUТ, вона мо­же порушуватися. Розглянемо проблему вибору дачі для літнього відпочинку за кри­теріями комфортності, наявності крамниці неподалік та віддалі від міста (табл. 1). Згідно з аксіомою незалежності, вибір децидента не має залежати від значень крите­рію «Відстань від міста», якщо їх значення є рівними для всіх альтернатив. Але ціл­ком можливою є ситуація, коли децидент обере альтернативу А, якщо за критерієм «Відстань від міста» обидва варіанти мають оцінку «Дача розташована близько від міста», і в той же час, якщо обидва варіанти мають за цим критерієм оцінку «Дача розташована далеко від міста», децидент обере альтернативу В.

Лотереї та побудова функцій корисності окремих критеріїв

Якщо виконано аксіоми першої групи та деякі з умов незалежності, то можна дійти висновку про існування багатокритерійної функції корисності певного вигляду.

Так, коли виконано умови незалежності за корисністю та перевагою, то згідно з тео­ремою Р. Кіні функція корисності адитивна чи мультиплікативна (7, 8),

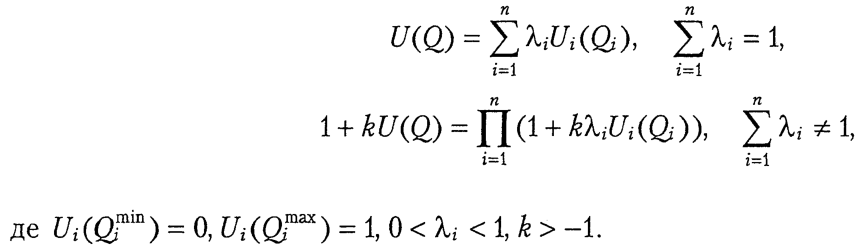
На отриманому теоретичному результаті ґрунтується метод, що широко використову­ється для розв'язання практичних задач. Проілюструємо етапи застосування МАUТ у ситуації вибору майданчика для будівництва летовища.

У зв'язку зі зростанням кількості та розширенням географії авіаперевезень у певному місті наявні біля нього летовища не впораються із суттєвим зростанням кількості авіапасажирів, тому потрібно побудувати нове летовище, яке відповідало б зрослим потребам.

Експертна група, основне завданням якої - обрати місце для нового летовища, визна­чила такі три основні критерії, щоб оцінювати різні варіанти його розміщення:

• вартість спорудження;

• відстань від міста;

• вплив шуму на людей, що мешкають поблизу летовища.

Бажано побудувати летовище із заданою пропускною здатністю за найменшу можли­ву вартість. Окрім того, потрібно, щоб переїзд пасажирів від летовища до міста й у зворотному напрямку займав якнайменше часу. Слід також мінімізувати кількість людей, що піддаються небажаним шумовим впливам. Звичайно ж, ці критерії супер­ечливі: спорудити летовище далеко від міста, імовірно, дешевше, хоча час поїздки в такому разі збільшується. Критерії відстані від міста й чисельності людей, які піддаю­ться шумовим впливам, також суперечливі.

Ця задача має такі особливості. По-перше, вона слабоструктурована. Якщо задачі з об'єктивними моделями слід розв'язувати здебільшого методами дослідження опера­цій, то ті, що схожі на наведену, потребують іншого підходу. Хоча всі критерії мають цілком зрозумілий об'єктивний зміст, а оцінки за критеріями - кількісне вираження, немає єдиної кількісної моделі, яка описувала б проблему загалом. Є лише набір із трьох суб'єктивно визначених експертною групою критеріїв. Потрібно обрати ту із за­даних альтернатив (місце для будівництва), для якої досягнуто найбажанішого з по­гляду експертної групи компромісу між критеріями. Для розв'язання таких задач бу­дують моделі, що описують переваги децидента (експертної групи). Ці моделі допо­магають зробити найкращий вибір.

Розглянувши критерії, експертна група визначила граничні межі зміни значень кри­теріїв (табл. 2). Це дає змогу почати будувати функцію корисності за кожним із критеріїв.

Таблиця 2. Діапазон змінення значень критеріїв спорудження летовища

Критерій	Найгірше значення	Найкраще значення
Q1 - вартість спорудження летовища Q2 - час переїзду до міста Q3 - кількість людей, що піддаються впливу шуму	400 млн дол. 90 хв 100 тис.	200 млн. дол. 40 хв 10 тис.

Максимальне значення функції корисності візьмемо рівним 1, а мінімальне — 0. По­будуємо функцію корисності для критерію Q₁. Напочатку відомі дві точки функції корисності: U(200) = 1 та U(400) = 0 (рис. 12). Оскільки значення вартості потрібно мінімізувати, на осі абсцис значення вартості відкладено у зворотному порядку - від 400 до 200.

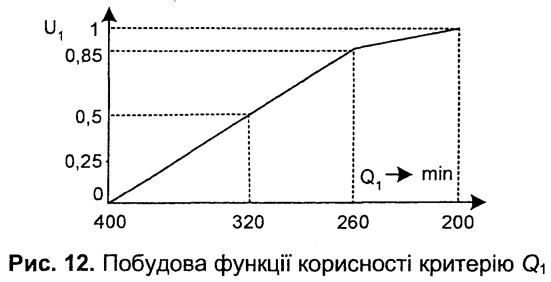
Для знаходження проміжних точок використовують лотереї. У лотереї 1 (рис. 13) децидент має знайти еквівалент визначеності для лотереї, яка має з однаковими ймо­вірностями 0,5 мінімальну та максимальну вартість спорудження.

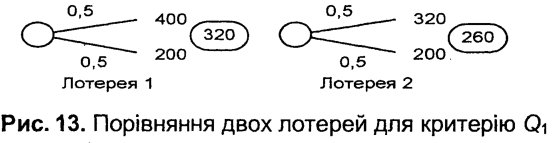
Із цією метою децидентові послідовно надають значення з певним кроком, близьким до його роздільної здатності (наприклад, 240 млн дол., $260 млн.), і запитують, де, на його думку, еквівалент визначеності - вище чи нижче, ніж задане значення. Якщо де­цидент зупинився на значенні 320 млн дол., то доходять висновку, що значенню U₁(Q₁) = 0,5 відповідає 320 млн дол. Аналогічно знаходять інші значення функції ко­рисності. Так, права лотерея на рис. 13 дає змогу визначити точку U₁(260) = 0,85. Ідентично будують функції корисності для інших критеріїв. Потім перевіряють умови незалежності за корисністю та перевагою.

Перевірку умови незалежності за корисністю можна сумістити з попереднім етапом побудови однокритерійних функцій корисності.

На рис. 14 наведено процес проведення лотереї 1. Спочатку децидентові повідомля­ють, що, шукаючи еквівалент, він має взяти до уваги, що решта критеріїв мають най­кращі значення. Потім перед ОПР ставлять ту саму задачу, але вже в припущенні, що всі інші критерії мають найгірші значення. Якщо еквівалент визначеності в обох ви­падках однаковий, то доходять висновку, що критерій не залежить за корисністю від інших критеріїв.

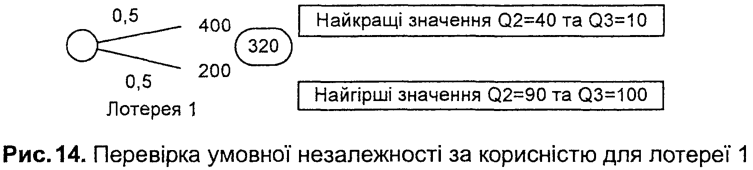
Для повноти перевірки умови незалежності за корисністю слід виконувати її для всіх лотерей. Проте в багатьох випадках проводять лише наближену перевірку — тільки для першої з лотерей, що використовуються для побудови однокритерійних функцій корисності.

Перевіряючи умови незалежності за перевагою, розглядають площини, де на осях по­дано значення двох критеріїв. Приклад такої площини для критеріїв Q₂ та Q₂ наведе­но на рис. 15. Спочатку припустімо, що інші критерії (тут - критерій Q₃) мають найкращі значення (Q₃ = 10).

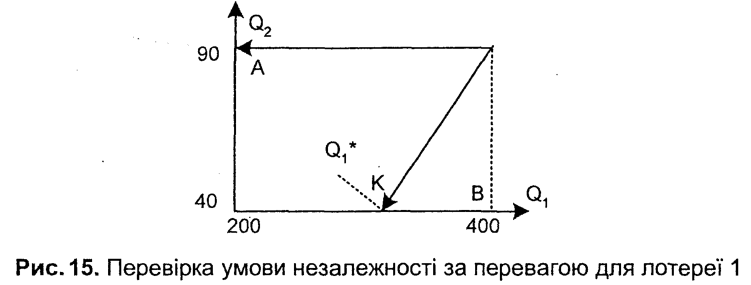
Спочатку децидент має визначити, якій із двох альтернатив ( ) або ( ) він віддає перевагу. їм відповідають точки А та В на рис. 15. Нехай де­цидент віддав перевагу альтернативі А перед В, тобто критерій вартості важливіший для нього, ніж критерій віддалі. Після цього на осі Q₁ децидент визначає точку К, якій відповідає таке значення критерію , що альтернативи А та К за умови Q₃ = 10 еквівалентні, тобто (200, 90) ~ ( , 40). Потім процедуру повторюють за умови Q₃ = 100. Якщо в обох випадках одержано одне й те саме значення то критерії та Q₂ незалежні за перевагою від критерію Q₃.

Для цілковитої впевненості умову незалежності за перевагою слід перевіряти для всіх пар критеріїв, хоча на практиці виконують наближену перевірку й обирають один або два найсуттєвіші критерії, а інші розглядають лише в парі з ними. Окрім того, для пе­ревірки незалежності використовують граничні значення критеріїв, вважаючи, що цього достатньо, хоча інколи не завадило б перевірити і проміжні значення.

Коли деякі з умов незалежності не виконуються, завдання побудови загальної функ­ції корисності суттєво ускладнюється. Єдиної відповіді про спосіб дій у цьому разі теорія не дає. Пропонується визначити групу незалежних критеріїв, важливості фун­кції корисності для підгруп залежних і незалежних критеріїв із побудовою функції корисності «частинами» чи переформулювати завдання.

І нарешті, коли побудовано функцію корисності за окремими критеріями, перевірено умови незалежності, і вони виконуються (хоча б наближено), для побудови загальної функції корисності потрібно отримати значення коефіцієнтів шкалювання при част­кових функціях корисності (коефіцієнти важливості критеріїв). Відношення між ва­гами критеріїв визначає децидент, шукаючи точки байдужості на площинах пар кри­теріїв. При цьому, на відміну від перевірки умов незалежності за перевагою, значення критеріїв упорядковують від гірших до кращих.

Розглянемо площину критеріїв (Q₁, Q₂), зображену на рис. 16. Альтернативи А та К перебувають у відношенні байдужості, яке визначають так само, як і в разі перевірки умови незалежності за перевагою.

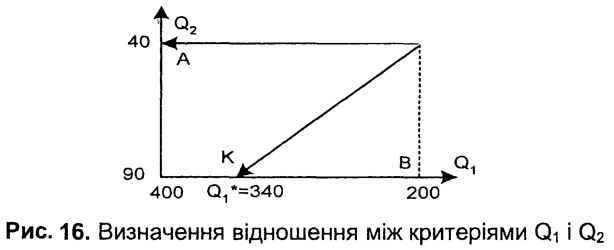
У точці рівноваги U(400, 40) = U(340, 90), тобто корисності альтернатив однакові. Звідси, використавши одержані раніше однокритерійні функції корисності, знайдемо λ₂=0,4λ₁

Аналогічно визначимо відношення між вагами критеріїв Q₁ та Q₃ унаслідок чого от­римаємо λ₃ = λ₁, U(300) = 0,6λ₁. Отже, ваги всіх критеріїв виражено через вагу най­важливішого з них, і критерії впорядковано за важливістю.

На відміну від прикладу 1, у якому для остаточного обчислення значень коефіцієн­тів шкалювання використано умову нормування, застосуємо трохи інший підхід, що ґрунтується на одержанні надлишкової інформації. Через це може бути порушена умова нормування. Для знаходження значення ваги критерію (і, отже, усіх крите­ріїв) дециденту пропонується порівняти дві стратегії (рис. 17) і знайти значення імовірності р за якого обидві стратегії рівнозначні.

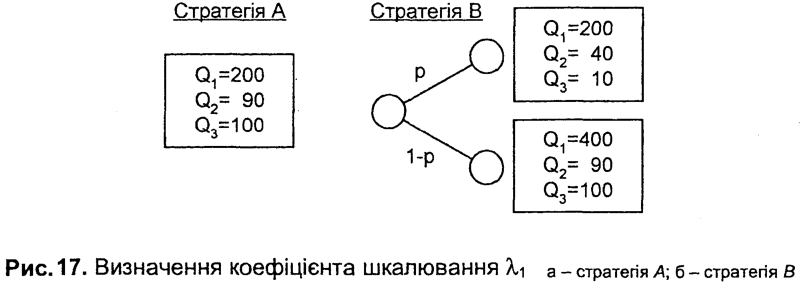
Після порівняння від децидента отримано значення р = 0,55. Оскільки U(А) = U(В), то λ₁ = р = 0,55, λ₂ ⁼ 0,22, λ₂ ⁼ 0,33. Тут умову нормованості коефіцієнтів шкалювання трохи порушено, тобто їх сума становить 1,1. У цьому разі, оскільки відхи­лення невелике, можна безпосередньо використовувати загальну функцію корисності з визначеними коефіцієнтами шкалювання чи, якщо потрібно, уточнити їх значення в повторному діалозі з децидентом.