49.Условие параллельности 2-х прямых в пространстве.

      ,имеет вид      

1)Если прямые параллельны, то они образуют с осью OX одинаковые углы. Поэтому угловые коэф-ты k1 и k2 этих прямых равны. Обратно, если  k1= k2,то углы наклона прямых  к оси OX одинаковы, откуда следует, что данные прямые параллельны. Условием параллельности 2-х прямых яв-ся равенство их угловых коэффициентов. (Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = l ,  ₁ = l .) 50.Условие совпадения2-х прямых в пространстве. Если  , т.е есл и , то 1"прямые либо совпадают:  , либо параллельны:  . Определить, какой из этих двухслучаев имеет место быть, очень просто. Если точка   лежит и на прямой  , т.е. ее координаты удовлетворяет уравнениям прямой  :  , то 1"прямые совпадают.

51.Условие пересечения 2-х прямых в пространстве.  Если  (не перпендикулярны), то 1"прямые либо скрещиваются, либо пересекаются. Если 1"прямые пересекаются, то обе они лежат в одной плоскости и, следовательно, векторы   компланарные ( прямые пересекаются в одной точке тогда и только тогда, когда  ) 52.Условие скрещивающихся прямых в пространстве. Если  (, не перпендикулярны), то 1"прямые либо скрещиваются, либо пересекаются,когда 1"прямые скрещиваются, векторы   некомпланарные. (1"прямые скрещиваются тогда и только тогда, когда  )

53.Угол между прямыми в пространстве.

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

   и      косинус угла между ними можно найти по формуле:

              =    .            

54.Условие параллельности прямой и плоскости

Прямая и плоскость параллельны тогда и только тогда, когда векторы 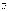  и   перпендикулярны.

{A,B,C}

55.Условие принадлежности прямой плоскости.

сли  , то уравнение (12.20) имеет вид  ; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств

является условием принадлежности прямой плоскости.

56.Условие ортогональности прямой и плоскости Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

условием перпендикулярности прямой и плоскости – условие параллельности этих векторов _{57.Задача о вычислении угла, образованного прямой и плоскостью.}

Угол θ между прямой и плоскостью есть угол между этой прямой и её проекцией на данную плоскость.

)= ; sin

Если направляющий вектор прямой выбрать так, чтобы cos,и взять 0 , то угол между прямой и плоскостью дополняет θ до

58) Матрицы. Виды матриц.

59) Линейные операции над матрицами

К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число). 

Умножение матрицы на число  При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:

Сложение матриц  Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || a_i j ||  и  B = || b_i j ||  является матрица  C = || c_i j || , элементы которой равны сумме соответствующих матричных элементов:

(3)

Линейной комбинацией матриц A и B называется выражение вида   , где     и    – числовые коэффициенты.

60) Сложение матриц. Свойства сложения

Суммой матриц   и   одинаковых размеров называется матрица   тех же размеров, у которой   Обозначение: C = А + В.

     Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0,   A, B, C.

61) Умножение матрицы на число и свойства умн.

  Произведением матрицы   на число   называется матрица   тех же размеров, у которой   Обозначение: 

     Свойства  ,       и 

62) Умножение матриц. Правило умн.

63) Свойства умножения матриц

64) Свойства определителя матрицы.

65) Алгебраическое дополнение к элементу матрицы.

66) Минор порядка к

Рассмотрим матрицу A:

  

Вычеркнем из матрицы k строк с номерами i1, i2, ..., ik и k столбцов, с номерами j1, j2, ..., jk.

Элементы, расположенные на пересечении вычеркнутых строк, образуют определиитель,

который называется минором порядка k. Его обозначают Mk:

67) Обратная матрица. Опр.

Квадратная матрица, определитель которой отличен от нуля, имеет обратную матрицу и притом только одну

A*- матрица,сост. из алг.дополнения к элеметам А.

Обра́тная ма́трица — такая 0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате 0%95%D0%B4%D0%B8%D0%BD%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0"единичную матрицу E:

:

68) Условия существования и единственности обратной матрицы.

Единственность обратной матрицы докажем от противного. Пусть кроме матрицы   существует еще одна обратная матрица   такая, что  . Умножая обе части этого равенства слева на матрицу  , получаем  . Отсюда  , что противоречит предположению  . Следовательно, обратная матрица единственная.