1)Принцип относительности

Скорость распостранения взаимоотноношения для описания процессов в природе неоходимо создать Систему отсчета. Под системой отсчета понимают оси координат для указания места положения частиц в пространстве и связанные с ним часы. Все законы природы одинаковы во всех инерциальных системах отсчета. Законы не меняют вид по отношению к преобразованию координат и ко времени к одной инерциальной системе и к другой.(формулы).опыт показал что мгновенного взаимодействия в природе не существует. В природе не существует сигналов распространяющихся с бесконечной скоростью. Из принципа следует, что что скорость распространения одинакова во всех инерциальных системах отсчета и она обозначается c(с=3*10(8))

В 1905 году Энштейн сформулировал принцип относительности: В нерелятивистской механике существует два понятия массы: первое относится ко второму закону Ньютона, а второе — к закону всемирного тяготения. Первая масса — инертная (или инерционная) — есть отношение негравитационной силы, действующей на тело, к его ускорению. Вторая масса — гравитационная — определяет силу притяжения тела другими телами и его собственную силу притяжения. Эти две массы измеряются, как видно из описания, в различных экспериментах, поэтому совершенно не обязаны быть связанными, а тем более — пропорциональными друг другу. Однако их экспериментально установленная строгая пропорциональность позволяет говорить о единой массе тела как в негравитационных, так и в гравитационных взаимодействиях. Подходящим выбором единиц можно сделать эти массы равными друг другу.

Иногда принцип равенства гравитационной и инертной масс называют слабым принципом эквивалентности. Идея принципа восходит к Галилею, и в современной форме он был выдвинут ещё Исааком Ньютоном, а равенство масс было проверено им экспериментально с относительной точностью 10⁻³. В конце XIX века более тонкие эксперименты провёл фон Этвёш^[8], доведя точность проверки принципа до 10⁻⁹. В течение XX века экспериментальная техника позволила подтвердить равенство масс с относительной точностью 10⁻¹²—10⁻¹³(Брагинский^[9], Дикке^[10] и т. д.).

2)Понятие события и интервала.

Эйнштейн пришел к необходимости рассматривать всё происходящее в окр мире в 4-х мерной системе отсчета, добавив к 3 пространственным координатам независимую переменную. (4-х мерное прос-во Минковского, 4-х мерный континиум).Точки 4-х мерного континиума соответстуют событиям - Точки наз мировым точкам. Траектория, описываемая движение- мировая линия. В этом прос-ве событиям опоставляются 4 координаты( 3 пространств., 1 временная) , кот при преобразовании меняются.Но сущ-ет величина инвариантная, относительно перехода от 1 к другой иннерц. Системы.- интервал.

В виду выражения для интервала 4-х мерный континиум Минковского харак-ся Евклидовой(гиперболической ) геометрией.

Все точки континиума по отношению к знаку ds² разбиваются на след области. ds²=c ² dt ²-dx ²-dy²-dz² >0

Линии свет конуса- линии, образ мировыми линиями лучей света, испущенными из т. О. t=0. ds²<0 времени подобные области. Точки будущего – точки, заполняющие верхнюю часть светового конуса. Образует область будущего для т. О Каждая точка будущего может явл следствием события 0.

ds2<0. Пространственно подобные области. Относительно них можно сделать утверждение – никакие точки не могут быть связаны мировой линией со скор большей скор света. В этом пространстве события сопоставляются

3)Собственное время. Парадокс близнецов. Допустим что мы в какой либо инерциальной системе движущиеся относительно нас часы (формулы)

Промежутки времени измеренные в движущиеся системе отсчета меньше промежутков времени измеренные в неподвижной системе отсчета

Парадокс: Формулировка I. С точки зрения домоседа часы движущегося путешественника имеют замедленный ход времени, поэтому при возвращении они должны отстать от часов домоседа. С другой стороны, относительно путешественника двигалась Земля, поэтому отстать должны часы домоседа. На самом деле братья равноправны, следовательно, после возвращения их часы должны показывать одно время.

4) ЛОРЕНЦА ПРЕОБРАЗОВАНИЯ в специальной теории относительности — преобразования координат и времени к.-л. события при переходе от одной инерциальной системы отсчёта .;. с. о.) к другой. Получены в 1904 голл. физиком X. А. Лоренцем H. A. Lorentz) как преобразования по отношению к к-рым ур-ния классич. микроскопич. электродинамики Лоренца — Максвелла уравнения) сохраняют свой вид. В 1905 их вывел . Эйнштейн, исходя из двух постулатов, составивших основу спец. теории относительности: равноправия всex и. с. о. и независимости скорости распространения света в вакууме от движения источника света. в специальной теории относительности - преобразования координат и времени к.-л. события при переходе от одной инерциалъной системы отсчёта (и. с. о.) к другой; выражают равноправие всех и. с. о. в описании законов природы. Впервые Л. п. были сформулированы в 1904 в связи с теоретич. и эксперим. работами по исследованию распространения света. Было установлено, что Максвелла уравнения сохраняют свою форму при Л. п. и, с другой стороны, Л. п. могут быть выведены как следствие (эксперим. факта) одинаковости скорости света в вакууме относительно произвольной системы отсчёта. В дальнейшем было осознано, что Л. п. имеют универсальный характер, являются матем. реализацией относительности принципами тем самым отражают общие свойства пространства и времени. Решающий шаг в этом направлении был сделан А. Эйнштейном (A. Einstein), важнейшую роль сыграли труды X. А. Лоренца, А. Пуанкаре (A. Poincare), Г. Минков-ского (Н. Minkowski).

Если и. с. о. К' движется относительно и. с. о. К с пост. скоростью V вдоль оси х, то Л. п. имеют вид

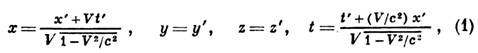
г де с - скорость света в вакууме. Ф-лы, выражающие через х, у, z, t, получаются из (1) заменой V на -V. В случае медленных движений (а) преобразования (1) приближённо переходят в преобразования Галилея: (на место а)

Л. и. (1) не совместимы с классич. (дорелятивистскими) представлениями о пространстве и времени. В классич. физике принимается, что понятие одновременности событий и, в частности, промежуток времени между двумя событиями (напр., между актами рождения и распада нестабильной частицы) имеют абс. смысл, т. е. они не зависят от движения наблюдателя

5)Формулы

Четырехвектор совокупность четырех величин которая при преобразовании четырехмерной системы отсчета преобразуются как компоненты четырех радиус векторов(х,y,z,t)

Два вида векторов:

1 сорт(контро-вариантные)

2 сорт (ко-вариантные)