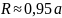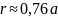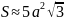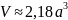- •Проект «Правильні многогранники»
- •II учень розв’язує задачу
- •Iіі учень доповідає інформацію «Геометрія галактик».
- •II учень демонструрє таблицю «Гексаедр» и робить доповідь.
- •III ученик розв’язує задачу
- •IV учень доповідає інформацію «цікаво знати» «Легенда про куб»
- •IV ученик выступает с информацией «Минералы»
- •Легенда об алмазе.
- •Правильные многогранники и природа
- •VI ученик выступает с информацией «Наука и жизнь»
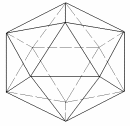
- •Икосаэдр
- •V группа с информацией «додекаэдр»
- •I ученик рассказывает «Факты и научные открытия», демонстрирует модель додекаэдра.
- •II ученик демонстрирует таблицу «Додекаэдр» и выступает с научной информацией.
- •III ученик решает задачу.
- •IV ученик выступает с информацией «в лучах кристалла Земли»
- •V ученик выступает с информацией «Правильные многогранники в живописи»
- •VI ученик выступает с исторической справкой «Памятник тем, кто не верит в математику»
IV ученик выступает с информацией «Минералы»
Что удивительно, некоторые кристаллы имеют форму правильных многогранников.
Кристалл соли (NaCl) имеет форму куба; бор - форму икосаэдра; сернистый колчедан (FeS) – форму додекаэдра; железо – форму куба; кристаллы золота – октаэдрический, кубической формы; кристаллы алмаза – октаэдры, кубы.
Правильные многогранники не только очаровывают нас своей привлекательностью. Оказывается, что они имеют много тайн, легенд, загадок.
Легенда об алмазе.
У арабов существует легенда.
В те далекие-далекие времена, когда Голубой Нил был так широк, что даже крокодилы не могли переплыть его, заспорило Золото с Алмазом, кто з них на Земле самый знатный, самый сильный.
- Я! – сказало Золото. – Меня отливают на короны султанов, шахов и королей, царицы носят чеканные золотые запястья на своих холеных руках, золотые кольца украшают их тонкие, подобные тычинка лотоса пальцы. Из-за меня на Земле пролито столько крови, что ею можно было бы наполнить все колодцы мира и озеро Чад. Ты, Алмаз, лишь ничтожный придаток к моей золотой славе.
- Ошибаешься, Золото, - возразил Алмаз, - из-за меня также велись кровопролитные войны, я тоже украшаю троны, скипетры и перстни фараонов, раджей и шахинь.
- Ну, если так, то давай спросим у Солнца, кто из нас могущественнее и ценнее, - предложило Золото, и они обратились со своим вопросом к вечному светилу.
- Я не слышу вас, - ответило Солнце. – Подойдите поближе и расскажите, о чем вы там спорите на своей померкшей звезде.
Тогда Золото и Алмаз пошли по Млечному Пути и приблизились к Солнцу. Но тут Золото покраснело, побледнело и, расплавившись, пролилось на Землю золотым дождем. А Алмаз вернулся таким же сверкающим и твердым, каким был прежде. С тех пор Золото никогда больше не спорило с Алмазом, раз и навсегда уступив ему пальму первенства.
Алмаз с греческого «несокрушимый».
Наиболее крупные алмазы имеют свои названия и историю.
Исторически первой формой огранки, появившейся в середине ХIV века, стал «октаэдр». Алмаз «Шах» почти сохранил свой естественный вид. Он имеет форму вытянутого кристалла – октаэдра, массу 88,7 карата и цвет воды с желто-бурым оттенком. В начале ХІХ века «Шах» оказался в Персии.
В 1829 году в ходе беспорядков в Тегеране был убит русский посол, автор комедии «Горе от ума» А. С. Грибоедов, и персидское правительство для разрешения конфликта подарило алмаз Николаю I.
IV группа с информацией «ИКОСАЭДР»
I ученик рассказывает «Факты и научные открытия», демонстрирует модель икосаэдра.
Геометрические объекты обладают свойствами гармонизации человека и пространства. Икосаэдр гармонизирует отношения с другими людьми, усиливает интеллект человека, выравнивает психику, восстанавливает связь человека с Землей.
II ученик демонстрирует таблицу «Икосаэдр» и выступает с научной информацией.
Фигура |
Элементы |
Количественные характеристики |
|
Вершин – 12 Ребер – 30 Граней - 20 |
где a – ребро икосаэдра
|
III ученик решает задачу 1.
Полная поверхность правильного тетраэдра с ребром a равновелика полной поверхности икосаэдра. Найдите ребро икосаэдра.
Решение
Если
ребро тетраэдра a,
то
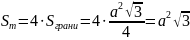
Если
ребро икосаэдра b, то
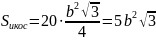
Если
полные поверхности тел равновелики, то
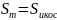
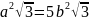
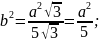
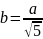
Ответ:
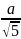
IV ученик решает задачу 2.
Дано правильный многогранник. Какой это многогранник?
Все грани – правильные треугольники;
Из каждой вершины выходит 5 ребер.
Варианты ответов:
(А) Данных (1) достаточно для решения задачи, а данных (2) недостаточно;
(Б) Данных (2) достаточно для решения задачи, а данных (1) недостаточно;
(В) И данных (1), и данных (2) достаточно для решения задачи;
(Г) Данных (1) и (2) ТОЛЬКО ВМЕСТЕ достаточно для решения задачи;
(Д) Данных (1) и (2) даже вместе НЕ достаточно для решения задачи.
V ученик выступает с информацией «Правильные многогранники и природа»