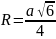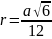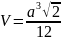Проект «Правильні многогранники»
Предмет: Геометрія, 11 класс.
«Тут поєднуються лід і полум’я»
О.Д.Олександров
Є в шкільному курсі геометрії теми, які чекаєш з нетерпінням, передчуваючи зустріч з неймовірно гарним матеріалом. До таких тем можна віднести "Правильні многогранники". "Правильних многогранників вражаюче мало, - писав Л. Керолл, але цей дуже скромний за чисельністю загін зумів увійти в самі глибини різних наук". Це той Льюіс Кэролл, який написав "Аліса в країні чудес". Але є у нього ще одна книга "Історія з вузликами", в якій він розглядав правильні многогранники і вигадував про них задачі.
І група учнів представляє з інформацією
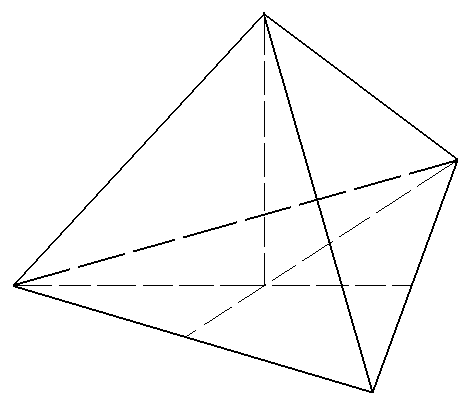
"ТЕТРАЕДР" І учень демонструє модель тетраедра і виступає з повідомленням. Назва «правильні многогранники» походить з Греції. Перше систематичне дослідження п'яти правильних тіл було зроблене ще піфагорійцями. Погляди піфагорійців детально викладені в трактаті Платона (427-347 р. до н.е.) "Тимей". Тому правильні многогранники називають також платоновыми тілами. Цим тілам присвячена 13-а книга "Начал" Евкліда.
Фігура |
елементы |
Кількісні характеристики |
|
Вершин – 4 Ребер – 6 Граней - 4 |
где a – ребро тетраедра |
II учень розв’язує задачу
Модель
молекули метану
має форму правильного
тетраедра, в
четырьох вершинах
якого знаходяться
атомы водню, а в
центрі – атом
вуглецю.
Визначити кут зв’язку між двомя
зв’язами.
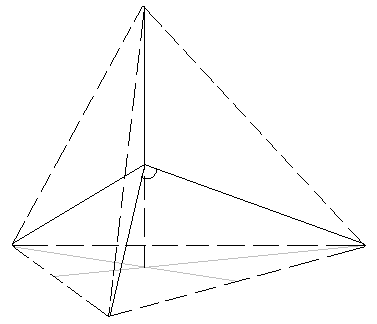H
C
φ
H H (D)
O
H (B)
Розв’язання У центрі тетраедра знаходиться атом водню. Геометрично: центр тетраедра є центром вписаної і описаної кулі біля тетраедра. А кут зв'язку між двома CH зв'язками - це кут BCD. Нехай
,
,
:
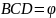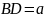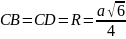
Согласно теоремы косинусов имеем:
,
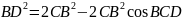
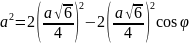
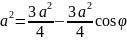
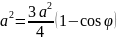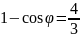
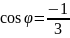
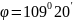
Відповідь:
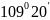
Iіі учень доповідає інформацію «Геометрія галактик».
Німецький астроном і математик Йоганн Кеплер(1571-1630) запропонував зв'язок між п'ятьма правильними многогранниками і шістьма відкритими на той час планетами Сонячної системи. Він мислив так: відомі шість планет, а правильних многогранників п'ять. І проміжків між планетами - п'ять. Це не випадково, між ними є зв'язок. Цей зв'язок астроном зображував так. Біля Сонця описував найбільшу сферу, по ній рухається Сатурн. У сферу орбіти Сатурну вписував куб, в який вписується сфера орбіти Юпітера. У неї вписується тетраедр, потім послідовно додекаедр, ікосаедр, октаедр. Така модель Сонячної системи дістала назву "Космічний кубок" Кеплера. Цікава історія з кубком: Кеплер звертається до герцога вюртембергского Фрідріха з проханням виготовити модель Всесвіту у вигляді срібного кубку по його, Кеплера, проекту. Фрідріх відповідає, що йому гроші не жаль, але він бажав би спочатку подивитися на цей кубок, зроблений з паперу. Кеплер зробив сам цей кубок.
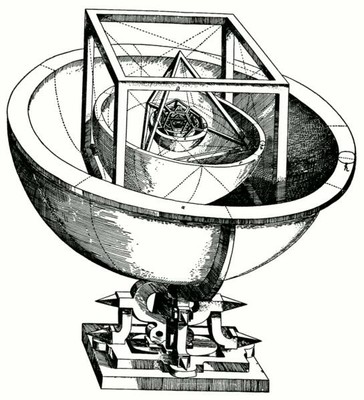
Гіпотез будови Всесвіту багато, але нас цікавлять тільки ті, які пов'язані з правильними многогранниками. Ось яку гіпотезу запропонували естонські математики і астрономи : "Всесвіт - це сукупність велетенських многогранників, утворених галактиками і супергалактиками". Вони вважають, що космічна речовина, яку ми називаємо зірками, рівномірно розподіляється в космічному просторі. У 1979 році в повідомленні естонських астрономів говорилося, що галактики витягнуті в ланцюжки, які утворюють велетенські осередки. Осередки мають форму правильних многогранників дуже великих розмірів - 200 млн. світлових років. По ребрах цих осередків сконцентроване 70% маси усіх галактик. Вони розміщуються на ребрах, гранях і вершинах. Сьогодні ця гіпотеза досліджується. II група з інформацією "ГЕКСАЕДР" I учень розповідає "Факти і наукові відкриття", демонструє модель
Гексаэдр – це куб.
Куб – (від лат. cubus, від греч. kybos – гральная кістка).
У китайців куб – божество Землі
У євреїв куб – Свята Святих
В ісламі Кааба – це куб, стабільність, статична досконалість
У майя куб – Земля, Древо Життя росте із центра кубу.