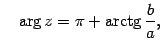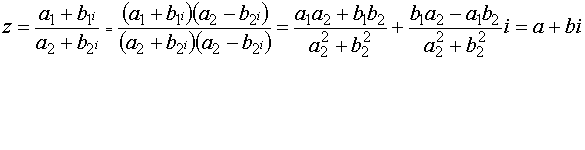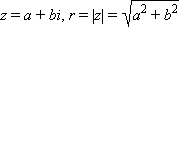- •Векторы. Операции над векторами и их свойства.
- •2. Определение линейной зависимости векторов.
- •3. Определение линейной независимости векторов.
- •4. Теоремы о линейной зависимости векторов.
- •7. Проекция вектора на ось.
- •12.Скалярное произведение векторов. Определение.
- •13. Свойства скалярного произведения.
- •14.Вычисление угла между векторами.
- •19. Векторное произведение векторов. Определение.
- •20. Свойства векторного произведения.
- •21. Геометрический смысл векторного произведения.
- •22. Задача о вычислении площади треугольника с помощью
- •23.Коллинеарные векторы. Определение.
- •26. Свойства смешанного произведения.
- •30.Условие компланарности векторов.
- •31. Вектороное произведение в декартовом базисе.
- •32. Смешанное произведение векторов в декартовом базисе.
- •33. Векторно параметрическое уравнение плоскости.
- •34. Вектрное уравнение плоскости.
- •Общее уравнение плоскости(координатная форма);
- •ПУсть:r0{x0;y0;z0},r{X,y,z},n{a;b;c}
- •41. Задача о вычислении угла, образованного пересекающимися плоскостями.
- •42. Векторно-параметрическое уравнение прямой в пространстве.
- •43. Каноническое уравнение прямой в пространстве.
- •1. Уравнение плоскости имеет вид
- •49.Условие параллельности 2-х прямых в пространстве. Условия параллельности и перпендикулярности прямых в пространстве
- •52. Условие скрещивающихся прямых в пространстве.
- •53. Угол между прямыми в пространстве.
- •54. Условие параллельности прямой и плоскости.
- •55. Условие принадлежности прямой плоскости .
- •60. Сложение матриц. Свойства операции сложения матриц.
49.Условие параллельности 2-х прямых в пространстве. Условия параллельности и перпендикулярности прямых в пространстве
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
Условие параллельности прямых L1 и L2, эквивалентное условию
коллинеарности векторов q1 и q2, заключается в пропорциональности
координат этих векторов, т. е. имеет вид
l1/l2=m1/m2=n1/n2
. (16.14)
Условие перпендикулярности прямых L1 и L2 может быть получено
из условия, что cosϕ = 0 и выражено равенством нулю скалярного
произведения q1 · q2. Оно имеет вид
l1l2 + m1m2 + n1n2 = 0. (16.15) 50. Условие совпадения2-х прямых в пространстве. Две прямые параллельны или совпадают тогда и только тогда, когда ихнаправляющие векторы коллинеарные:
 .
.
51. Условие пересечения
2-х прямых в пространстве. Условие
пересечения 2-х прямых в пространстве.
Если прямые
![]() и
и
![]() пересекаются, то они лежат в одной
плоскости, следовательно, в одной
плоскости должны лежать векторы:
пересекаются, то они лежат в одной
плоскости, следовательно, в одной
плоскости должны лежать векторы:
![]() ,
,
![]() ,
,
![]() .
.
необходимое и достаточное условие пересечения двух прямых и принимает вид:
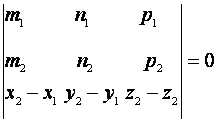
52. Условие скрещивающихся прямых в пространстве.
Если условие не выполнено, то прямые и скрещиваются.
53. Угол между прямыми в пространстве.
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
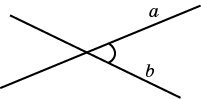
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.

Две прямые называются перпендикулярными,
если угол между ними прямой. Угол
![]() находится по формуле
находится по формуле
 ,
где
,
где
![]() - направляющий вектор.
- направляющий вектор.
![]() - нормаль к плоскости.
- нормаль к плоскости.
54. Условие параллельности прямой и плоскости.
прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.
55. Условие принадлежности прямой плоскости .
1) Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
2) Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.
58. Матрицы. Виды матриц. Матрицей называется прямоугольная таблица чисел, состоящая из mодинаковой длины строк или n одинаковой длины стробцов. основные виды матриц: Квадратная – в которой число строк равно числу столбцов (m=n) Нулевая – все элементы этой матрицы равны 0. Транспонированная матрица — матрица В, полученная из исходной матрицы A заменой строк на столбцы. Единичная – все элементы главной диагонали равны 1, все остальные 0. Обра?тная ма?трица — матрица
59. Линейные операции над матрицами.
1. Равенство матриц
2. Умножение матрицы на число
3. Сложение матриц
60. Сложение матриц. Свойства операции сложения матриц.
Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || является матрица C = || ci j || , элементы которой равны сумме соответствующих матричных элементов:
|
|
66. Минор порядка k. Определение. Минор порядка k (по лекциям) - определитель матрицы, составленный из k строк и k столбцов матрицы. Минор порядка k (по инету) - определитель матрицы, составленный из элементов данной матрицы, стоящих на пересечении произвольно выделенных её k строк и k столбцов с сохранением их порядка, то есть минор k-го порядка - определитель квадратной матрицы k*k.
67. Обратная матрица. Определение. Обраная матрица - такая матрица (А^-1), при умножении на которую, исходная матрица (А) даёт в результате единичную матрицу (Е): А * А^-1 = A^-1 * A = E
68. Условие существования и единственности обратной матрицы. Условие существования обратной матрицы/(критерий обратимости). А^-1 существует, когда detA не равен 0 Доказательство: Предположим, А^-1 существует => A^-1 * A = E => det(A^-1 * A) = detE => detA^-1 * detA = 1 => detA^-1 <> 0 и detA <> 0.
69. Формула для нахождения обратной матрицы. А^-1 = 1/detA * A c волнистой линией наверху транспанированное
70. Решение матричного уравнения AX=B с помощью оюбратной матрицы А^-1 * (AX) = A^-1 * B (A^-1 * A) * X = A^-1 * B E * X = A^-1 * B X = A^-1 * B
81. Многочлены. Теорема Безу. многочлен - функция, значение которой в любой точке может быть найдено с помощью конечного числа сложений и умножений. Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен (x-a) равен P(a). Доказательство P(x)/(x-a)=>остаток P(a) (с этой строчкой осторожнее но он сказал все теоремы так “озаглавливать” ну подобно) Поделим с остатком многочлен P(x) на многочлен (x-a) : P(x)=(x-a)Q(x)+R(x) Так как degR(x)<deg(x-a)=1 , то R(x) — многочлен степени не выше 0. Подставляя x=a , поскольку (a-a)Q(a)=0 , имеем P(a)=R(a) . Следствие Число a является корнем многочлена p(x) тогда и только тогда, когда p(x) делится без остатка на двучлен x-a (отсюда, в частности, следует, что множество корней многочленаP(x) тождественно множеству корней соответствующего уравнения P(x)=0 ).
82. Формулировка Основной теоремы алгебры. Основна́я теоре́ма а́лгебры утверждает, что Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
83. Понятие комплексного числа. «Мнимая» единица. Комплекстным числом в алгебраической форме называется число z=x+yi где xy –любое действительное число. Мнимая единица-комплекстное число квадрат которого равен -1 84 Z=x+yi 85 Рассмотрим на плоскости декартову прямоугольную систему координат . Каждому комплексному числу можно сопоставить точку с координатами , и наоборот, каждой точке с координатами можно сопоставить комплексное число . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплекные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью. Изобразим на комплексной плоскости числа z1=2+i,z2=3i ,z3=-3+2i ,z4=-1-i ,z5=-3
Однако чаще комплексные числа изображают в виде вектора с началом в точке , а именно, комплексное число изображается радиус-вектором точки с координатами . В этом случае изображение комплексных чисел из предыдущего примера будет таким:
Пусть комплексное число z=a+bi изображается радиус-вектором. Тогда длина этого вектора называется модулем числа z .
Угол, образованный радиус-вектором числа z с осью Ox , называется аргументом числа z и обозначается argz . Аргумент числа определяется не однозначно, а с точностью до числа, кратного 2Pi . Однако, обычно аргумент указывают в диапазоне от 0 до 2pi или в диапазоне от -Po до Pi . Кроме того у числа z=0 аргумент не определен.
Из того же рисунка следует что
С помощью этого соотношения можно
находить аргумент комплексного
числа: причем первая формула действует, если изображение числа z находится в первой или четвертой четверти, а вторая, если -- во второй или третьей. Если a=0 , то комплексное число изображается вектором на оси Oy и его аргумент равен Pi/2 или 3pi/2 .
86. Операция сложения комплексных чисел в алгебраической форме. Алгебраическая форма комплексных чисел Пусть x и y – обычные числа. Число вида z=x+iy называется комплексным числом в алгебраической форме. По аналогии со сложением и вычитанием векторов мы приходим к следующему правилу сложения и вычитания комплексных чисел:
(a1 + b1i ) + (a2 + b2i ) +...+ (an + bni ) = (a1 + a2 + ...+ an ) + (b1+ b2+...+ bn ) i = Ao + Bi Вычитание определяется как действие, обратное сложению, то есть разность x + iy = (a1 + b1i) – (a2 + b2i ) То есть (a1 + b1i ) – (a2 + b2i ) = (a1 – a2 ) + (b1– b2) i.
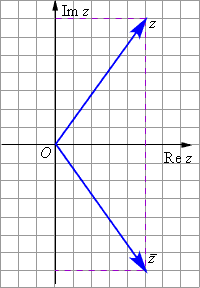
87. Операция умножения комплексных чисел в алгебраической форме. Правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены. Умножение двух комплексных чисел производится как умножение обычных чисел, надо лишь помнить, что : i^2=-1 (a1 + b1i ) * (a2 + b2i)=(a1*a2+a1*b2i+b1i*a2-b1*b2)=(a1*a2-b2*b1)+(b1a2+a1b2)i (http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2421.gif) //малоли кто в электронном виде будет читать. 88. Если число z = a + bi, то число называется комплексно сопряжённым с числом z. их модули равны, а фазы равны по модулю но имеют противоположные знаки. произведение комплексно-сопряженных чисел есть действительное число равное квадрату модуля этих чисел. Векторное представление комплексно-сопряженных чисел представлено на рисунке.
89. Операция деления комплексных чисел в алгебраической форме. Алгоритм. Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di
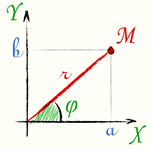
90. Тригонометрическая форма комплексного числа. Модуль и аргумент комплексного числа. Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i, называется аргументом комплексного числа a + b·i
Часто бывает удобна другая форма записи комплексного числа. Пусть:
Тогда по определению аргумента имеем:
Отсюда получается z = a + bi = r(cos φ + i sin φ).
95. Показательная формула комплексного числа. Z=|z|*(cosϕ+isinϕ)=|z|e^iϕ
96. Формула Эйлера. e^iϕ =cosϕ+isinϕ (где e-основание натурального логарифма, i-мнимая единица) 97. Связь между тригонометрической и показательной формами комплексного числа. Показательная и тригонометрическая функции связаны между собой формулой Эйлера 98.Операция умножения комплексных чисел в показательной форме. При произведении комплексных чисел модули перемножаются , а аргументы складываются Z1*Z2=|z|*|z|*( cosϕ1+ isinϕ1)*( cosϕ2+isinϕ2)=|z1|*|z2|*( cosϕ1* cosϕ2- sinϕ1* sinϕ2+i(cosϕ1* sinϕ2+ sinϕ1* cosϕ2)=|z1|*|z2|*(cos (ϕ1+ϕ2)+isin (ϕ1+ϕ2)) 99.Операция деления комплексных чисел в показательной форме. При делении комплексных чисел модули делятся а аргументы вычитаются Z1\Z2=|z1|\|z2|*(cos (ϕ1- ϕ2)+isin(ϕ1- ϕ2)) 100.Операция возведения в степень комплексного числа в показательной форме. Z^n=|z|^n*(cosnϕ+isinnϕ) Пример: Z^2=z*z=|z|*|z|*(cos (ϕ+ϕ)+isin(ϕ+ ϕ))=z^2*(cos2ϕ+isin2ϕ)
|
|

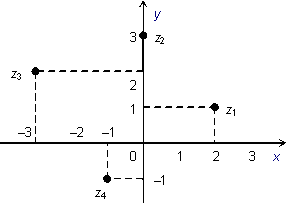

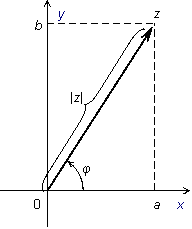 Из
рисунка следует
Из
рисунка следует

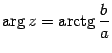 или
или