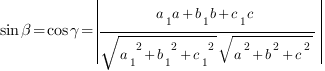43. Каноническое уравнение прямой в пространстве.
Пусть М1(x1, y1, z1)
– точка, лежащая на прямой l,
и 
–
её направляющий вектор. Возьмём на
прямой произвольную точку М(x,y,z)и
рассмотрим вектор 
.
Векторы
и
коллинеарные,
поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,
– канонические уравнения
прямой.
45. Уравнение прямой на плоскости. Геометрический смысл коэффициентов в уравнении. Любую прямую на плоскости можно задать уравнением прямой первой степени вида A x+ B y+ C= 0 ,где A и B не могут быть одновременно равны нулю. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: Уравнение прямой с угловым коэффициентом Общее уравнение прямой при B≠0 можно привести к виду y = k x+ b,где k- угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ Уравнение прямой в отрезках на осях Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках x + y = 1 a b (строчки выше, это типо икс делить на а + игрик делить на б равно 1) Уравнение прямой, проходящей через две различные точки на плоскости Если прямая проходит через две точки A(x1, y1) и B(x2, y), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямой можно найти, используя следующую формулу Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.
46. Взаимное расположение прямых на плоскости.
Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2. Теорема 1. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1= lВ. Если еще и С1 = lС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы двух уравнений. |
Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
48. Угол между прямыми на плоскости. Опреление угла на плоскости. Для этого нам, как обычно, понадобятся некоторые теоретические сведения.
1. Уравнение плоскости имеет вид
2. Важно! В
этом уравнении плоскости коэффициенты 
–
координаты вектора нормали к плоскости (то
есть вектора, перпендикулярного
плоскости).
3.
Косинус угла между векторами 
и 
вычисляется
по формуле:
4. Любой
ненулевой вектор 
,
лежащий на прямой 
,
или параллельный прямой
,
называется направляющим
вектором прямой.
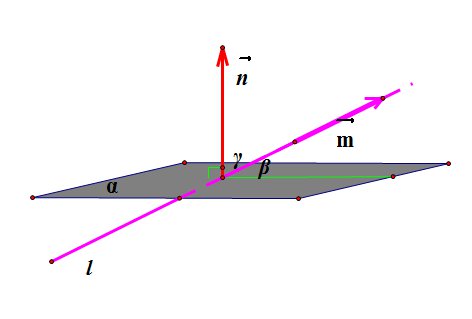
5. Синус
угла 
между
прямой
и
плоскостью 
равен
косинусу угла 
между
нормалью (
)
к плоскости и направляющим вектором
прямой (
),
поскольку эти два угла в сумме равны
90°.
То
есть синус угла
между
прямой, направляющий вектор которой
имеет координаты
и
плоскостью, заданной уравнением
вычисляется
по формуле:
