30.Условие компланарности векторов.
Три вектора компланарны если их смешанное произведение равно нулю.
Три вектора компланарны если они линейно зависимы.
31. Вектороное произведение в декартовом базисе.
_ _ _ _ _
ахв =|i j k|
|α α2 α3|
|β β2 β3|,
где
_
a( α,α2,α3)
_
b(β, β2, β3)
32. Смешанное произведение векторов в декартовом базисе.
_ _ _
(axb)c=|α α2 α3|
|β β2 β3|
|λ λ2 λ3|
Где
_
a(α;α2;α3)
_
b(β;β2;β3)
_
c(λ;λ2;λ3)
33. Векторно параметрическое уравнение плоскости.
Пусть в координатном
пространстве 
заданы:
а) точка 
;
б) два неколлинеарных вектора (рис.4.15).
Требуется
составить параметрическое уравнение
вида (4.10) плоскости, компланарной
векторам 
и
проходящей через точку 
Выберем
на плоскости произвольную точку 
.
Обозначим 
-радиус-векторы
точек
и
(рис.4.16).
Точка 
принадлежит
заданной плоскости тогда и только тогда,
когда векторы 
и 
компланарны.
Запишем условие компланарности: 
где 
—
некоторые действительные числа
(параметры). Учитывая, что 
получим векторное
параметрическое уравнение плоскости:
где
—
направляющие векторы плоскости, а 
—
радиус-вектор точки, принадлежащей
плоскости.
Координатная форма записи
уравнения называется параметрическим
уравнением плоскости:
34. Вектрное уравнение плоскости.
_ _ _
(r-r0)*n=0
_ _ _ _
r*n-r0*n=0
_ _
r*n-D=0
_ _
r*n=D
35.
Общее уравнение плоскости(координатная форма);
_ _ _
ПУсть:r0{x0;y0;z0},r{X,y,z},n{a;b;c}
_ _ _
запишем(r-r0)*n=0 b подставим
A(x-x0)+b(y-y0)+C(z-z0)=0
Ax-Ax0+By-By0+Cz=0
Ax+By+Cz-D=0
41. Задача о вычислении угла, образованного пересекающимися плоскостями.
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Под углом между
двумя плоскостями будем понимать один
из двугранных углов, образованных этими
плоскостями. Очевидно, что угол между
нормальными векторами 
и 
плоскостей
α1 и
α2 равен
одному из указанных смежных двугранных
углов 
или 
.
Поэтому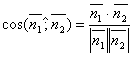 
.
Т.к.
и 
,
то
.
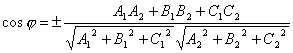42. Векторно-параметрическое уравнение прямой в пространстве.
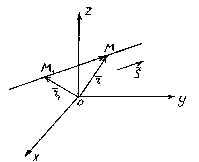Положение
прямой в пространстве определяется
заданием какой-либо её фиксированной
точки М1 и
вектора 
,
параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть
прямая l проходит
через точку М1(x1, y1, z1),
лежащую на прямой параллельно вектору 
.
Рассмотрим
произвольную точку М(x,y,z) на
прямой. Из рисунка видно, что 
.
Векторы 
и 
коллинеарны,
поэтому найдётся такое число t,
что 
,
где множитель t может
принимать любое числовое значение в
зависимости от положения точки M на
прямой. Множитель t называется
параметром. Обозначив радиус-векторы
точек М1 и М соответственно
через 
и 
,
получаем 
.
Это уравнение
называется векторно-параметрическим уравнением
прямой. Оно показывает, что каждому
значению параметра t соответствует
радиус-вектор некоторой точки М,
лежащей на прямой.
Далее идет параметрическое уравнение прямой*
(Запишем
это уравнение в координатной форме.
Заметим, что 
, 
и 
отсюда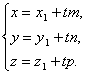 
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.)