19. Векторное произведение векторов. Определение.

20. Свойства векторного произведения.

21. Геометрический смысл векторного произведения.

По определению длина векторного произведения векторов  

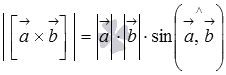
длина векторного произведения векторов   и   равна площади параллелограмма со сторонами   и   и углом между ними, равным 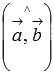 . В этом состоит геометрический смысл векторного произведения.

22. Задача о вычислении площади треугольника с помощью

векторного произведения. Чтобы найти площадь треугольника, нужно векторное произведение 2-х векторов разделить на 2 или умножить на 1/2:

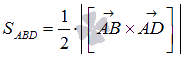
23.Коллинеарные векторы. Определение.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору. Коллинеарные векторы могут иметь одно и то же направление (сонаправленные) или противоположное.

24.Условие коллинеарности векторов. Либо такой ответ на вопрос: Условия коллинеарности векторов

• Два вектора коллинеарные, если отношения их координат равны.

• Два вектора коллинеарные, если их векторное произведение равно нулю.

Либо так: Два ненулевых вектора   и   коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

для коллинеарности двух ненулевых векторов   и   на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениям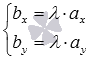и:   или  .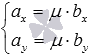

Для коллинеарности двух ненулевых векторов   и   в пространстве необходимо и достаточно, чтобы 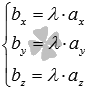  или  .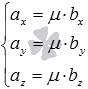

25.Смешанное произведение векторов. Определение. Смешанным произведением называется скалярное произведение 3-его вектора на векторное произведение первых двух.

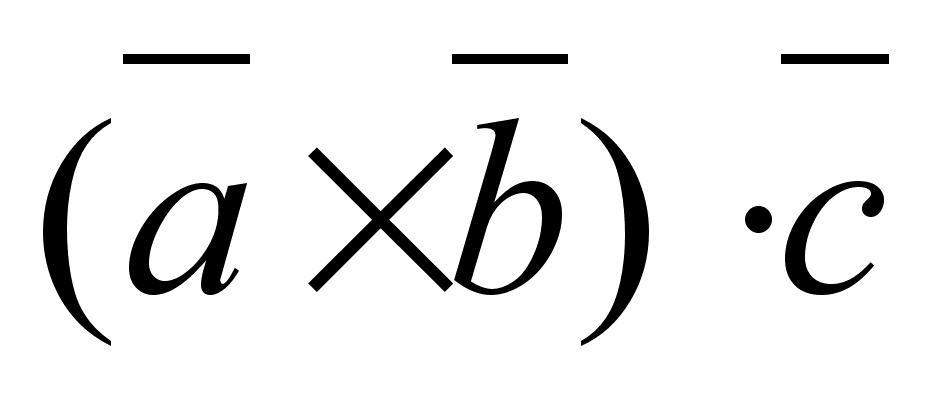
26. Свойства смешанного произведения.

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b)•с=(b х с)•а=(с х а)•b .

2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).

3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .

4. Смешанное произведение ненулевых векторов а, b и с равно нулю тогда и только тогда, когда они компланарны.

26. Свойства смешанного произведения. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

28. Задача о вычислении обьёма пирамиды с помощью смешанного. Задание. Вычислить объем пирамиды, построенной на векторах

  ,  , 

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов ,   и  :

29. Компланарные векторы. Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.