1. Векторы. Операции над векторами и их свойства.

Операции над векторами.

Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c - его диагональю.

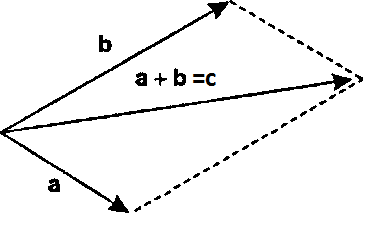
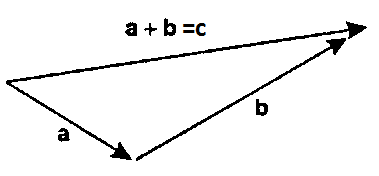
Сложение векторов в соответствии с предыдущим рисунком называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из следущего рисунка. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.

Произведением вектора a на вещественное число называется вектор b, определяемый условием :

1) a ll b

2) lbl = l l * lal

3) векторы b и a направлены одинаково, если , и противоположно, если

при = 0 из 2 условия следует, что lbl=0, то есть вектор b = нулевому вектору.

Свойства векторов.

2. Определение линейной зависимости векторов.

3. Определение линейной независимости векторов.

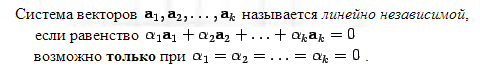
4. Теоремы о линейной зависимости векторов.

5. Базис в пространстве. Декартов базис.

6. Декартова система координат. Декартова система координат- совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат– и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

7. Проекция вектора на ось.

Ось - прямая линия с указанным на ней направлением и с началом отсчета.

Проекцией вектора ᾱ на ось L – длина вектора, начало и конец которого получены с помощью проецирования на ось L начала и конца вектора ᾱ. Проекции вектора на координатные оси называются также его (декартовыми) координатами. Координаты X, Y, Z определяются по формулам X=x2-x1, Y=y2-y1, Z=z2-z1.

Если α, β , γ  - углы, которые вектор составляет с координатными осями, то, cosα, cosβ, cosγ,  называются направляющими косинусами вектора.

X=|ᾱ|*cosα , Y=|ᾱ|*cosβ , Z=|ᾱ|*cosγ

cos^2α+ cos^2β+ cos^2γ = 1

8. Геометрический смысл координат вектора.

Координаты вектора это длины проекций вектора на соответствующие оси.

9. Геометрический смысл линейной зависимости 2-х векторов.

Система e ₁, e ₂, ... , e _m n-мерных векторов называется линейно зависимой, если найдутся такие числа l₁ , l₂ , ... , l_m , из которых хотя бы одно отлично от нуля, что выполняется равенство l₁ e ₁ + l₂ e ₂ +... + l_m e _m = 0. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

10. Геометрический смысл линейной зависимости 3-х векторов.

Система e ₁, e ₂, ... , e _m n-мерных векторов называется линейно зависимой, если найдутся такие числа l₁ , l₂ , ... , l_m , из которых хотя бы одно отлично от нуля, что выполняется равенство l₁ e ₁ + l₂ e ₂ +... + l_m e _m = 0. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

11. Линейная зависимость 4-х векторов.

Четыре вектора всегда образуют линейно зависимую систему.

        Доказательство.     Если первые три вектора являются компланарными, то они образуют линейно зависимую подсистему. Следовательно, вся система линейно зависима. Если первые три вектора - некомпланарные, то четвертый является их линейной комбинацией. Исходя из того что: «Система векторов линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.» данная система является линейно зависимой.