4.5. Рычажные механизмы и механизмы прерывистого действия

В приборах наиболее широкое распространение получили трёх- и четы­рёх­звенные рычажные механизмы. К ним относятся синусный, тангенс­ный, поводковый, кривошипно-ползунный, четырёхшарнирный, кулисный и другие механизмы.

Синусный и тангенсный механизмы служат обычно для пре­об­­ра­­зо­вания прямолиней­ного поступательного перемещения толкателя 1 во вращение рычага 2 (рис.29). В синусном механизме (рис.29, а) на торцевую плоскость толкателя 1 опирается рычаг 2 с шаровой рабочей поверхностью.

₀



S

O

2

1

r

₀



S

2

1

a

В

О

а)

б)

B

S₀

Рис.29. Синусный (а) и тангенсный (б) механизмы

Длина рычага остаётся практически постоянной, поэтому характеристика передачи (соотношение между входной и выходной величинами) имеет вид

S = r (sin - sin₀),

где ₀=const- угол между прямой ОВ и начальным положением рычага; -угол между прямой ОВ и конечным положением рычага.

Передаточное отношение от толкателя 1 к рычагу 2 находим как пер­вую производную от S по , то есть u₁₂ = r cos .

В тангенсном механизме (рис. 29, б) толкатель 1 имеет закруглённый конец, а рычаг 2 имеет плоскую поверхность. В этом механизме расстояние а остаётся неизменным, поэтому характеристика механизма и его пере­да­точное отношение имеют вид

S = a (tg - tg₀), u₁₂=dS/d=a/cos².

Таким образом, передаточные отношения в синусном и тангенсном механизмах являются переменными, а регулировка их значений осуществ­ляется изменением начальных размеров r и a и начальных углов ₀ наклона рычага 2 .

Синусный и тангенсный механизмы совместно с зубчатыми применяются в микроскопических измерительных го­лов­ках (индикаторах), кинема­ти­ческая схема одной из которых предс­тавлена на рис.30. В схеме механизма имеется две зубчатые пары, с одним из зубчатых колёс жёстко связана стрелка 3 длиной L, а передаточное отноше­ние, связываю­щее линейное перемеще­ние конца стрелки с углом  поворота второго рычага 2,

u_2-5 = L z₁ z₃/(z₂z₄).

Связь между углом поворота  второго рычага длиной r₂ и перемещением

S толкателя описывается характеристикой

 = arcsin[l S₀/(r r₂)] - arcsin[l(S₀-S)/(r r₂)]+ + arcsin(S/r) - arcsin[(S₀ - S)/r].

Поводковый механизм относится к прост­ранственным механизмам. На рис. 31, а показан поводковый меха­низм, сос­тоящий из двух валиков 1 и 2, к которым жёстко прикреплены повод­ки 3 и 4. Чаше других применяются по­вод­ковые механизмы с валиками и повод­ками, расположенными под углом 90 друг к другу. Траекторией точки каса­ния поводков будет прямая NЕ, яв­ля­ю­щаяся следом пересечения двух взаимно перпендикулярных плоскос­тей, в кото­рых происходит движение поводков.

Характеристика поводкового механизма имеет вид

S=NE= a tg = b tg.

Иногда для получения заданного характера шкалы прибора ведущий поводок наклоняют под углом  (рис. 31, б). В этом случае ось поводка 3 будет описывать коническую поверхность, а траектория точек касания поводков будет гиперболой, являющейся следом пересечения плоскости движения поводка 4 с конической поверхностью.

Передаточное отношение поводковой передачи - величина переменная, зависящая от угла  и длин а и b. Если a=b и =0, то u=1 при всех значениях .

На рис. 32 показана схема переда­точ­ного механизма манометра, у кото­рого звенья 1(мембранная короб­ка) и 8 образуют тангенсный механизм, валики 4 и 7 с поводками 5 и 6 обра­зуют поводковую передачу и зубчатый

м

2

3

4

5

6

7

8

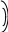
еханизм типа сектор-шестерня - звенья 2 и 3. Такая схема даёт возможность получить значитель­ный угол поворота на выходном звене 2 при небольшом угле поворота вала 7.

Рис.32. Схема переда­точ­ного механизма манометра

1

Кривошипно-ползунный механизм. Кинематическая схема и принцип работы механизма рассмот­рены ранее (см.рис.23). Параметрами, опреде­ля­ю­щими кинема­тику этих механизмов, являются отно­ше­ния длин криво­шипа, шатуна и эксцентриситета.

Рис.33. Кинематические схемы выпрямляющих рычажных механизмов

Наибольшее применение в самопишущих и других приборах получили выпрямляющие рычажные механизмы, у которых одна из точек выходного звена на некотором участке своего движения описывает траекторию, близкую к прямой. На рис. 33 приведены примеры схем таких механизмов с прямолинейным движением точки D : а- кривошипно-ползунный механизм, у которого АВ=ВС=ВD; б- лямбдообразный механизм Чебышева с размерами звеньев АЕ=2ВЕ; АС=ВС=DC= 2,5 BE; в- кулисный механизм: АС=АВ; ВD=3,4AB.

Механизмы прерывистого действия служат для преобразования враща­тель­ного, обычно равномерного, или колебательного непрерывного движе­ния в движение вращательное или поступательное с периодическими оста­новками определённой продолжительности. Применяются механизмы с мальтийским крестом, цевочные, кулачковые, с неполными зубчатыми колёсами, храповые и др.

Мальтийские механизмы применяются для преобразования обычно рав­но­мерного вращательного движения ведущего звена-кривошипа в перио­дические повороты с остановками определённой продолжительности ведо­мо­го звена-креста. Кпд механизма 0,75-0,85.

Механизм с внешним зацеплением и четырёхпазовым крестом показан на рис. 31. Ведущим звеном всегда является кривошип 1, а ведомым - крест 2. Число радиальных пазов z может быть от 3 до 12.

При вращении кривошипа 1 цевка А входит в паз креста 2 и поворачивает его на угол 2/z. Когда цевка А выходит из паза, крест останавливается и фик­сируется секторным замком. Выпуклая цилиндрическая поверхность замка вхо­дит в соприкосновение с вогнутой поверх­ностью креста и препятствует повороту последнего до тех пор, пока цевка А кривошипа не войдёт в следующий паз креста. За один полный оборот кривошипа с одной цевкой крест делает 1/z оборота и остановку.

Основные геометрические параметры

мальтийских механизмов (рис.34): межосевое расстояние L, радиус кривошипа R₁, число пазов z креста, расчётные радиусы креста R_2max, R_2min , углы ₀=/z и ₀=/2- ₀.

Кинематические параметры мальтийских механизмов:

- период цикла движения Т, равный времени одного оборота кривошипа;

- коэффициент движения К= t_Д/Т=₀/, где t_Д- время движения креста за один период его цикла движения;

- угловые скорости и ускорения движения креста.

Наибольшая угловая скорость креста соответствует положению меха­низма, при котором цевка А находится на линии центров О₁ О₂ (рис.34). При этом

_2max = ₁ R₁/ R_2max = ₁ u_max = ₁ sin₀/(1-sin₀) .

Угловые ускорения креста в начальный и конечный моменты его движения

_2нач = _2кон =  ₁² R₁/R_2max = ₁² tg₀.

Из анализа формул видно, что угловое ускорение креста тем меньше, чем меньше угловая скорость движения кривошипа, меньше ₀ (или больше число пазов креста z). Следовательно, для уменьшения сил инерции масс, связанных с крестом, и динамических нагрузок на детали механизма целесообразно увеличивать z.

Критериями работоспособности мальтийских механизмов являются:

- точность изготовления и сборки;

- прочность и жёсткость оси ролика цевки;

- износостойкость рабочих поверхностей пазов креста, ролика и оси цев­ки.

Конструктивно узел оси и ролика цевки кривошипа может выполняться в виде пары с трением скольжения или с трением качения. Размеры узла устанавливаются из конструктивных соображений. Длина В полоски контакта ролика цевки и креста проверяется на соответствие условию контактной прочности по формуле Герца-Беляева

 _Н = 0,418  P_max Е_пр/(В r_p)  _Н,

где Е_пр- приведённый модуль упругости материалов ролика и креста, r_p- радиус ролика цевки, _Н- допускаемое контактное напряжение, для закалённых поверхностей из стали 50 или 40Х _Н=10001200 МПа, Р_mах -наибольшая сила, действующая на ось ролика цевки кривошипа при положении её на линии центров О₁О₂ ,определяется по формуле

Р_mах=М_{1 mах}/R₁,

где М_{1 mах} - максимальный момент на валу кривошипа, складывается из статического момента сил сопротивления и динамического момента, связанного с инертностью деталей. Наибольший статический момент на валу кривошипа

М_{1 mах} = М_{1 ст max} + М_{1дин mах} = М₂ u _max/+ I₂_{2 max} u_max/,

где - кпд механизма, I₂-момент инерции креста механизма.

Для обеспечения износостойкости рабочих поверхностей пазов креста, ролика и оси цевки проверяется условие ограниченности давления р (МПа)

р=Р_mах/(l d₀)  [p],

г де l и d_0­- длина и диаметр трущихся поверхностей оси и ролика, мм, [p]=1520 МПа- допускаемое давление.

Ось цевки кривошипа проверяется на прочность при изгибе:

 = М _И /W = P_max (h+0,5B) / (0,1d³)  [].

Храповые механизмы (рис.35) ис­поль­зуются для преобразования коле­бательного дви­жения ведущего звена 1 во враща­тельное (или поступательное) дви­жение с оста­новками ведомого звена 2. Кроме того, они применяются как ме­х­анизмы, пре­пят­ству­ющие движению ведо­мых звеньев в одном нап­рав­лении и допускающие сво­бод­ное

движение их в проти­воположном направлении. Чис­ло зубьев колеса 2 определяется наи­мень­шим углом поворота его за один ход собачки 3.

Критерием работоспособности храповых механизмов является прочность оси собачки и контактная прочность собачки в местах её контакта с осью и зубьями храпового колеса. Исходя из этого рассчи­тывается длина зуба колеса, равная отношению окружной силы к допуска­емому удельному давлению на единицу длины контакта зуба колеса и собачки.