10.Векторное произведение векторов, его модуль

Векторное произведение векторов 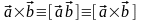- вектор, со следующими свойствами: 1. , 2. , . Модуль векторного произведения – это площадь параллелограмма, построенного на векторах-сомножителях, равная:

Компоненты векторного произведения вычисляются по следующей формуле, которая легко получается из приведенных выше свойств этого произведения:

=

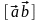
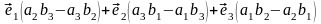
Двойное векторное произведение вычисляется по формуле «бац минус цаб»:

12.Радиус-вектор, координаты точки

Для начала рекомендуем ознакомиться с материалом статьи прямоугольная система координат на плоскости и в пространстве.

Зададим прямоугольную декартову систему координат Oxy на плоскости и отложим от начала координат векторы   и  , направление которых совпадает с положительными направлениями осей Ox и Oy соответственно.

Определение.

Векторы   и   называются координатными векторами данной системы координат.

Теперь от начала координат отложим произвольный вектор  . В силу геометрического определения операций над векторами, вектор   можно представить в виде  , причем коэффициенты   и   определяются единственным образом, что легко доказывается методом от противного.

Определение.

Представление вектора   в виде   называется разложением вектора  по координатным векторам   и   на плоскости.

Определение.

Коэффициенты   и   называются координатами вектора в данной системе координат на плоскости.

Координаты вектора в данной системе координат будем записывать через запятую в круглых скобках, отделяя их от обозначения вектора знаком равенства. К примеру, запись  означает, что вектор   имеет координаты   в заданной системе координат Oxy и раскладывается по координатным векторам   и   как  .

Обратите внимание: порядок записи кординат имеет значение! Вектор с координатами   отличен от вектора  .

Очевидно  , так как разложения координатных векторов имеют вид  .

Нулевой вектор   на плоскости имеет координаты равные нулю  , так как  .

Пусть векторы   и   равны. Тогда они совпадут, если их отложить от начала координат. Следовательно, их разложения по координатным векторам будут иметь один и тот же вид. Поэтому 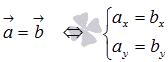 , то есть, соответствующие координаты равных векторов равны.

Координаты противоположного вектора   противоположны соответствующим координатам вектора  , то есть,  .

Аналогично определяются координаты вектора в прямоугольной системе координат, заданной в трехмерном пространстве: вводится тройка координатных векторов  , произвольный вектора   раскладывается по ним единственным образом как  , а коэффициенты этого разложения   называются координатами вектора   в данной системе координат.

Координатные векторы в трехмерном пространстве имеют координаты  , координаты нулевого вектора равны нулю  , соответствующие координаты равных векторов равны  , а координаты противоположного вектора   противоположны соответствующим координатам вектора  , то есть,  .

К началу страницы

Координаты радиус-вектора точки.

А сейчас остановимся на очень важном моменте - покажем связь координат точки и координат вектора в данной системе координат.

Пусть в прямоугольной декартовой системе координат Oxy на плоскости задана произвольная точка  .

Определение.

Вектор   называется радиус-вектором точки М.

Выясним, какие координаты имеет радиус-вектор точки в данной системе координат.

Вектор   представляется в виде суммы  , где точки  и   есть проекции точки М на координатные оси, а   и   - координатные векторы, следовательно, вектор   имеет координаты   в данной системе координат. Другими словами, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки   разлагается по координатным векторам   как  , следовательно,  .