1)

2 Дифференциалом функции   в   называется главная, линейная относительно  , часть приращения функции.

.

Покажем, что   и   эквивалентные бесконечно малые при  :

(  - бесконечно малая).

Геометрический смысл дифференциала:

Пр оведем к графику функции   в точку   касательную   и рассмотрим ординату этой касательной для точки  . На рисунке  ,  . Из прямоугольного треугольника   имеем:  , т.е.  . Но, согласно геометрическому смыслу производной,  . Поэтому   или  . Это означает, что дифференциал функции  в   равен приращению ординаты касательной к графику функции в этой точке, когда   получает приращение  .

Приближенные вычисления:

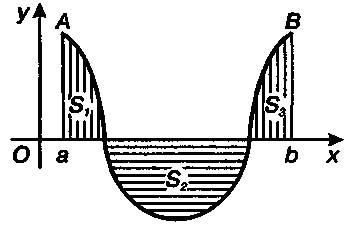
3 Геометрический смысл определенного интеграла

Если а < b, f(x) >= 0, то

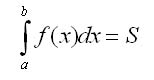
т.е. определенный интеграл от функции у = f(x) по отрезку [а, b] равен площади криволинейной трапеции, ограниченной сверху графиком функции у = f{x), слева и справа - отрезками прямых х = а, х = b, снизу — отрезком оси Ох (см. рис.). В контрольных работах по математике задание на нахождение определенного интеграла задают очень часто.

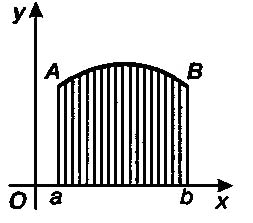
Если а < b и f(x) <= 0, то

т. е. определенный интеграл от функции, принимающей неположительные значения, равен площади соответствующей криволинейной трапеции, взятой со знаком минус (см. рис.).

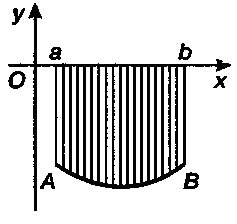
Если а < b и f(х) меняют знак на отрезке [а, b], то определенный интеграл равен алгебраической сумме площадей соответствующих криволинейных трапеций.

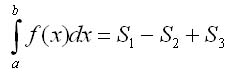
4) Определение. Векторная величина, или вектор — это физическая величина, характеризуе-

мая: 1) неотрицательным скаляром; 2) направлением в пространстве. При этом скаляр на-

зывается модулем вектора, или его абсолютной величиной.

Сложение векторов

В физике можно складывать только векторы, обладающие одинаковой размерностью. Мы мо-

жем складывать скорость со скоростью, силу с силой, но не имеем права сложить вектор ско-

рости с вектором силы.

Правила сложения векторов можно объяснить на двух характерных примерах: сложении

перемещений и сложении сил.

5 Модуль вектора – это длина отрезка, заключенного между двумя точками: точкой начала вектора и точкой его конца. А это ни что иное, как расстояние между двумя этими точками. Поэтому чтобы найти расстояние между любыми двумя точками, нужно вычислить модуль вектора, соединяющего эти точки.

компоненты вектора – это просто координаты конечной точки вектора.

6  

7 Выражение скалярного произведения векторов через их компоненты

8 Проекция одного вектора на другой.

проекция вектора А на вектор В = (A,B)/|B| где (A,B) скалярное произведение векторов А и В |B| - длина вектора В если A=(a1,a2), B=(b1,b2) тогда (A,B)=a1*b1+a2*b2 |B|=sqrt(b1^2+b2^2)

  Определение 10.23   Проекцией вектора b на вектор a,   , будем называть проекцию вектора b на любую ось, параллельную вектору a и имеющую направление, совпадающее с направлением вектора a.         

Проекция вектора b на вектор a обозначается   .

Очевидно, что   , где    -- угол между векторами a и b.

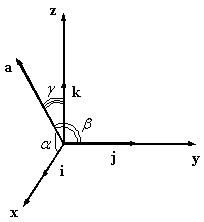
Рис.10.23.Направляющие косинусы вектора

В соответствии с рис. 10.23, направляющими косинусами вектора a являются   ,   ,   .

        Предложение 10.17   Координаты вектора равны его направляющим косинусам, умноженным на длину вектора. Если вектор единичный, то его координатами служат направляющие косинусы.

Проекция вектора на ось

Пусть задан вектор   и некоторая ось   с единичным вектором  . Точки   и   - проекции точек   и   на ось  соответственно.

Определение

Проекцией вектора   на ось   называется длина отрезка  , взятая со знаком "+", если направление   совпадает с направлением вектора  , и со знаком "-", если направление   противоположно направлению единичного вектора оси   (рис. 1).

Проекция вектора   на ось   обозначается символом  .