Аффинные криптосистемы.

К р и п т о стойкостью называется характеристика шифра, определяющая его устойчивость к дешифрованию без знания ключа.

Более высокую криптостойкость по сравнению с шифром Цезаря имеют аффинные криптосистемы. В таких системах за счет математических преобразований буквы, заменяющие открытый текст, относительно хаотично перемешаны.

Буквы алфавита нумеруются числами, например от 0 до 32. Затем каждая буква открытого текста заменяется буквой, порядковый номер в алфавите которой вычисляется с помощью линейного уравнения,

Аффинные криптосистемы задаются при помощи двух чисел: а и Ь. Для русского алфавита эти числа выбираются из условия о<a, Ь < 32. Причем числа а и у т 33 должны быть взаимно простыми. Если это условие не будет выполняться, то две разные буквы могут отобразиться в одну. Каждый код (номер в алфавите) буквы криптограммы определяется по коду буквы открытого текста по следующему правилу. Вначале вычисляется число , a затем выполняется операция целочисленного деления числа а на число . Математически это записывается так: , что означает: является остатком от целочисленного деления а на у. Число Р используется ;в качестве кода буквы шифрограммы. Для определенности выберем такие числа

Фрагмент расчета порядковых номеров букв криптограммы и соответствие букв и их порядковых номеров (кодов) приведены в таблице:

Предположим, что нужно зашифровать сообщение «ГДЕ АББА». В результате

Повысить криптостойкость позволяют шифры многоалфавитной, или многозначной, замены. В таких шифрах каждому символу открытого алфавита ставят в соответствие не один, а несколько символов шифровки.

Ниже приведён фрагмент ключа многоалфавитной замены

Для каждой буквы исходного алфавита создается некоторое множество символов шифрограммы так, что каждое из этих множеств не содержит одинаковых элементов.

С помощью многоалфавитного шифра сообщение «ГДЕ АББА» можно зашифровать несколькими способами:

Таблица Виженера.

Рассмотрим еще один шифр многоалфавитной замены, который был описан в 1585 г. французским дипломатом Блезом де Виженером. Шифрование производится с помощью Так называемой таблицы Виженера: Здесь показана лишь часть таблицы для того, чтобы »(9лрж?ть,лишь; идею метода.

Каждая строка в этой таблице соответствует одному шифру, простой замены (наподобие шифра Цезаря). При шифровании сообщения его записывают в строку, а под ним помещают ключ. Если ключ оказывается короче сообщения, то ключ циклически повторяют. Шифровку получают, находя символ в матрице букв шифрограммы на пересечении, столбца с буквой открытого текста и строки с соответствующей буквой ключа.

Таблица Виженера. _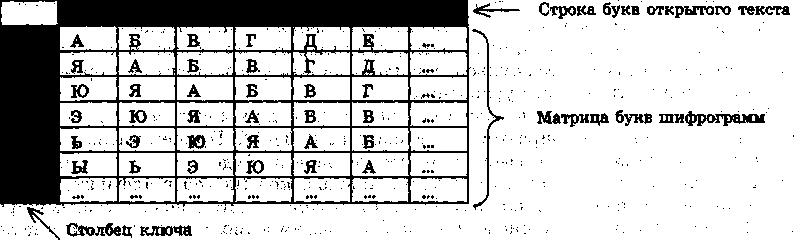

Предположим, что нужно зашифровать сообщение «ГДЕ АББА». В качестве ключа выберем слово «ДЕВА». В результате получим:

Квадрат Бьюфорта.

Существует, конечно, много других легко запоминающихся квадратов, которые могут применяться в качестве основы для многоалфавитной системы так же, как и таблица Виженера. Один из наиболее известных таких квадратов — квадрат Бьюфорта: его строками являются строки таблицы Виженера, записанные в обратном порядке.

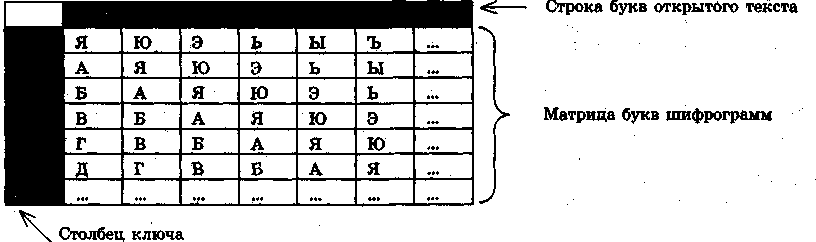
Квадрат Бьюфорта:

Предположим, что нужно зашифровать сообщение «ГДЕ АББА». В качестве ключа выберем слово «ДЕВА». В результате получим:

Система Плейфейра.

Еще одним шифром многоалфавитной замены является система Плейфейра, которая названа в честь барона Плейфейра. Рассмотрим основную идею этой, системы.

Шифрование производится с помощью квадрата (или прямоугольника), в который занесены в произвольном порядке буквы соответствующего национального алфавита. Порядок занесения букв и конфигурация таблицы составляют в совокупности секретный ключ. Для определенности возьмем прямоугольную таблицу размером 4 х 8, в качестве букв алфавита —кириллицу, а буквы расположим в алфавитном порядке. Так как число русских букв — 33, а число клеток — 32, исключим из таблицы букву Ё.

Предположим, что требуется зашифровать слово «КРИПТОГРАФИЯ». Рассмотрим правила шифрования.

1. Открытый текст делится на блоки по две буквы. Число букв в тексте должно быть четным. Буквы в одном блоке не должны быть одинаковыми. Произведем разделение исходного слова: КР-ИП-ТО-ГР-АФ-ИЯ.

2. Если буквы из пары букв шифруемого текста находятся в разных строках и столбцах, то в качестве заменяющих букв используются буквы, которые расположены в углах прямоугольника, охватывающего буквы открытого текста. Например, блок КР заменяется символами ИТ. 3. Если пара букв открытого текста попадает в одну строку, то шифрограмма получается путем циклического сдвига вправо на одну клетку. Например, блок ИП будет преобразован в ЙИ, а блок КН — в блок ЛО.

4. Если обе буквы открытого текста попадают в один столбец, то для шифрования осуществляют циклический сдвиг на одну клетку вниз. Так, блок ЖЦ будет преобразован в символы ОЮ, а блок ТЪ — в символы ЪВ.

В соответствии с описанными правилами слово «КРИПТОГРАФИЯ» будет преобразовано в криптограмму ИТЙИЦКАУДРПШ.

Заметим, что если блоки открытого текста состоят из одинаковых букв, то криптограмма тоже будет содержать одинаковые пары символов. По этой причине рассмотренный шифр относится к одноалфавитным. Однако модификация этого шифра превращает его в многоалфавитную систему. Для этого используется несколько таблиц Плейфейера и производится многократное шифрование.