Изучение криптографии на уроках информатики

Проблема защиты информации от несанкционированного (самовольного) доступа (НСД) заметно обострилась в связи с широким распространением локальных и особенно глобальных компьютерных сетей.

Защита информации необходима для уменьшения вероятности утечки (разглашения), модификации (умышленного искажения) или утраты (уничтожения) информации, представляющей определенную ценность для ее владельца.

Проблема защиты информации от постороннего доступа и нежелательных воздействий на нее возникла давно. С развитием человеческого общества, появлением частной собственности, государственного строя, борьбы за власть и дальнейшим расширением масштабов человеческой деятельности информация приобретает цену. Ценной становится та информация, обладание которой позволяет ее существующему и потенциальному владельцам получить какой-либо выигрыш — материальный, политический, военный и др.

Проблема защиты информации очень актуальна в настоящее время в России. В учебных заведениях необходимо готовить специалистов, которые занимались бы данной проблемой, и открывать новые специальности. Часть вопросов может быть изучена в рамках школьной программы по информатике. Основные вопросы, рассматриваемые в данной статье, касаются обзора, классификации методов криптографии и разработки заданий для учащихся и студентов.

Обзор методов криптографии Шифр атбаш.

Проблема защиты информации волнует людей несколько столетий.

Коды появились в глубокой древности в виде криптограмм (что в переводе с греческого означает «тайнопись»). Порой священные иудейские тексты шифровались методом замены. Вместо первой буквы алфавита писалась последняя буква, вместо второй — предпоследняя и т. д. Этот древний шифр назывался атбаш.

Шифр Цезаря.

Известен факт шифрования переписки Юлия Цезаря (100 — 44 гг. до н. э.) с Цицероном (106 — 43 гг. до н. э.). Шифр Цезаря реализуется заменой каждой буквы в сообщении другой буквой этого же алфавита, отстоящей в алфавите от данной буквы на фиксированное число букв. В своих шифровках Цезарь заменял букву исходного открытого текста буквой, расположенной по отношению к исходной букве на три позиции вперед.

Под шифрованием понимается такое преобразование информации, которое делает исходные данные нечитаемыми и трудно раскрываемыми (дешифруемым и) без знания специальной секретной информации — ключа. В результате шифрования открытый текст превращается в шифрограмму и становится нечитаемым без использования дешифрующего преобразования. Шифрограмма может называться иначе: зашифрованный текст, криптограмма, шифровка или шифротекст. Шифрограмма позволяет скрыть смысл передаваемого сообщения.

Предположим, что требуется зашифровать сообщение «ГДЕ АББА». Шифр Цезаря называется циклическим потому, что при выполнении замены буквы алфавита рассматриваются как расположенные по кругу: вслед за последней буквой алфавита вновь следует первая буква алфавита. Покажем, как выполняется шифрование шифром Цезаря:

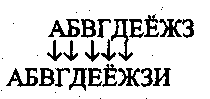
В результате проведенного преобразования получится шифрограмма ЁЖЗ ГДДГ.

Квадрат Полибия.

В Древней Греции (II в. до н. э.) был известен шифр, который создавался с помощью квадрата Полибия. Для шифрования использовалась таблица, представляющая собой квадрат с пятью столбцами и пятью строками, которые нумеровались цифрами от 1 до 5. В каждую клетку такой таблицы записывалась одна буква. В результате каждой букве соответствовала пара чисел, и шифрование сводилось к замене буквы парой цифр.

Идею квадрата Полибия проиллюстрируем таблицей с русскими буквами. Число букв в русском алфавите отличается от числа букв в греческом алфавите, поэтому и размер таблицы выбран иным (квадрат 6 х 6). Заметим, что порядок расположения символов в квадрате Полибия является секретным ключом. Под к л ю ч о м понимается секретная информация, определяющая, какое преобразование из множества возможных шифрующих преобразований выполняется в данном случае над открытым текстом.

Зашифруем с помощью квадрата Полибия слово «КРИПТОГРАФИЯ»: 26 36 24 35 42 34 14 36 11 44 24 63

Из примера видно, что в криптограмме первая цифра указывает номер строки, а вторая — номер столбца.