2.5. Шифр четырех квадратов

Шифр четырех квадратов — биграммный шифр, изобретен Феликсом Деластеллом. Для шифрования используются четыре матрицы размером 5х5 (для латинского алфавита) или 6х6 (для русского алфавита)

организованные в виде квадрата. При этом верхняя левая и правая нижняя матрицы содержат стандартный упорядоченный алфавит, а правая верхняя и нижняя левая представляют собой матрицы, называемые квадратами шифротекста. Для создания таких квадратов сначала необходимо заполнить каждый из них ключевым словом или фразой, отбрасывая повторяющиеся символы, а затем оставшимися символами алфавита. При этом заполнение может производиться любым способом. Например, слева-направо построчно или спиралью от левого верхнего угла.

Для шифрования выберем два ключевых слова: 1) алгоритм, 2) шифрование. Пусть необходимо зашифровать сообщение «Секретность ключа.» Алгоритм выглядит следующим образом:

1. Составить четыре квадрата в соответствии с правилами, описанными выше, и выбранными ключевыми словами.

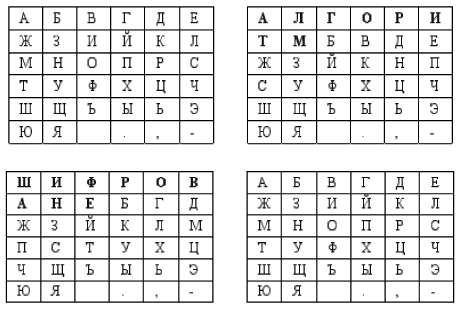
2. Разбиваем исходное сообщение, которое необходимо зашифровать на биграммы:

«СЕ» «КР» «ЕТ» «НО» «СТ» «Ь » «КЛ» «ЮЧ» «А.»

3. Первая буква биграммы ищется в левой-верхней матрице, вторая буква биграммы в правой-нижней.

4. Нечетная буква зашифрованного текста находится в той же строке, что и первая буква шифруемой биграммы, и в том же столбце, что и вторая буква шифруемой биграммы, то есть на их пересечении.

5. Аналогично находится четная буква зашифрованного текста. Удобно при шифровке представлять себе прямоугольник с известной левой-верхней и правой-нижней вершинами: левая-нижняя вершина — четная буква шифротекста, а правая-верхняя — нечетная. По этим правилам зашифрованный текст примет вид:

«ПВДЛАЦЙЗЖЦЪ,ЕГ-ПОЮ»

Расшифровка аналогична дешифровке шифра Уинстона (все операции, которые применялись для шифрование, выполняются в обратном порядке.

2.6. Шифры простой замены

2.6.1 Шифр простой замены

В шифре простой замены каждый символ исходного текста заменяется символом из того же алфавита одинаково на всем протяжении текста. При этом есть некоторая таблица соответствий (или любая другая структура), которая описывает пары символов (а,b): а — заменяемый символ шифруемого сообщения, b — символ, на который заменяется а, причем устанавливается взаимнооднозначное соответствие. Часто шифры простой замены называют шифрами одноалфавитной подстановки.

Расшифровка шифра простой замены очень проста и заключается в обратной подстановке b на a.

Пример.

Пусть необходимо зашифровать текст «Секретность ключа».

Шифр простой замены. Выберем алфавит подстановки для шифра простой замены, произвольно записав пару для каждой неповторяющейся буквы шифруемого сообщения:

2.6.2 Шифр Цезаря

Шифр Цезаря является частным случаем шифра простой замены. При шифровании исходного текста каждая буква заменяется на другую букву того же алфавита путем смещения по алфавиту от исходной буквы на k букв. При достижении конца алфавита выполняется циклический переход к его началу.

Рассматривая алфавит криптосистемы как множество целых Z_m, мы можем записать функцию шифрования Е(х) для некоторого k в шифре Цезаря как:

Е(x) = (x + k) mod m, для любого х принадлежащего Z_m,

где x - числовой код буквы открытого текста; x+k -числовой код соответствующей буквы шифротекста; m — количество букв в алфавите (его мощность).

Очевидно, что функция дешифрования D(x) для некоторого k записывается как:

D(x)= (x + m-k) mod m, для любого x принадлежащего Z_m,

Операция сложения по модулю m, заключается в следующем: если результат операции больше m, то от результата необходимо отнимать т до тех пор, пока не получится число меньше либо равное модулю m. То есть если шифруется буква «Э», x для которой равно 30, и k выбрано равным 10, результат сложения по модулю 32 (мощность русского алфавита) равен 8 ( (30+10) mod 32=40 mod 32= 40-32=8, что меньше 32).

Пример.

Пусть необходимо зашифровать сообщение: «Секретность ключа». Выберем k=10. Заполним таблицу:

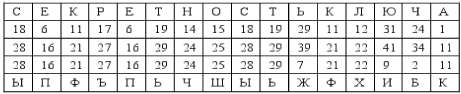
Первая строка представляет собой шифруемое сообщение. Вторая строка — порядковые номера букв исходного сообщения в алфавите. Символы третьей строки получены из символов второй путем прибавления к ним k=10. Четвертая строка содержит символы третьей взятые по модулю. Пятая представляет собой результирующую шифровку.

Расшифровка заключается в следующем. Выписывается шифротекст и порядковые номера его символов в алфавите. От каждого номера символа отнимается k=10. Если результат операции получился отрицательный, необходимо прибавить значение модуля m. После чего надо перевести полученные положительные коды в сообщение, что даст нам исходную посылку.

Также встречается много алфавитный шифр Цезаря. В отличие от простого, он образуется множеством одноалфавитных подстановок, определяемых функциями шифрования Е(х) для различных значений ключа k, причем 0 < k < m, где m-мощность алфавита.

2.6.3 Шифр Цезаря с ключевым словом

Особенностью этого шифра является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановки.

Алгоритм шифрования выглядит следующим образом. Выписывается алфавит. Затем под буквами алфавита записывается ключевое слово, начиная с буквы, числовой код которой совпадает с выбранным числом k. Для соблюдения правила взаимнооднозначного соответствия необходимо, чтобы все буквы ключевого слова были различны (если это не так, можно исключить повторяющиеся). Буквы алфавита подстановки, не вошедшие в ключевое слово, записываются после ключевого слова в алфавитном порядке. Получается подстановка для каждой буквы произвольного сообщения.

Пример.

Пусть необходимо зашифровать текст: «Секретность ключа». Выберем для шифрования ключ «Криптография».

Зашифрованный текст: «ЛОБЙОМЕЖЛМЫ БВЭЦК»

Задание по теме «Защита информации»

Написать программу, позволяющую зашифровать свою фамилию, имя и отчество, записанные через пробел (русскими или латинскими буквами) с использованием заданного в Вашем варианте метода шифрования и затем расшифровать. Вывести в выходной файл исходный текст, подлежащий шифрованию, зашифрованное сообщение, расшифрованный текст, а также другую информацию, поясняющую процесс шифрования (ключи, таблицы и т.п.).

Варианты задания:

1. перестановочный шифр с ключевым словом,

2. магический квадрат,

3. шифр Кардано,

4. полибианский квадрат (зашифрованное сообщение буквенное),

5. полибианский квадрат (зашифрованное сообщение числовое),

6. шифрующая таблица Тритемиуса,

7. шифр бифид (bifid),

8. шифр трифид (trifid),

9. шифр Цезаря,

10. шифр Цезаря с ключевым словом.