1.5. Шифр Кардано
Был разработан в середине 16 века итальянским математиком Кардано. В основе него лежит идея использования части самого передаваемого открытого текста в качестве ключа и новый способ шифрования, получивший название «решетка Кардано». Для ее изготовления берется квадратный кусок картона в котором по специальным правилам прорезаются «окна». При шифровании решетка накладывается на лист бумаги и открытый текст вписывается в окна. Затем решетка поворачивается на 90 градусов и вновь вписывается текст, всего 4 раза. Главное требование к «решетке Кардано» - при всех поворотах окна не должны попадать на одно и то же место бумаги. При этом если остаются пустые места, они заполняются произвольными буквами, а затем шифрограмма выписывается построчно.
Пример: Необходимо зашифровать текст: «Секретные ключи.»
Выберем решетку Кардано и то, как мы будем ее поворачивать для шифрования ( в данном случае по часовой стрелке):
В
результате зашифрованное сообщение
примет вид: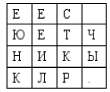
Получатель должен иметь такую же решетку Кардано, что использовалась при шифровании (с аналогично прорезанными «окнами»). Он записывает полученное сообщение построчно в таблицу, размер которой соответствует имеющейся решетке. Затем получатель накладывает на записанное в таблицу сообщение решетку в положении, соответствующем первоначальному при шифровании, и выписывает символы из «окон». После чего, необходимо повернуть решетку на 90 градусов и снова выписать полученные символы. Операция поворота в общей сложности должна быть выполнена три раза.
Во всех рассмотренных алгоритмах перед шифрованием можно удалить пробелы и знаки препинания.
2. Подстановочные шифры (шифры замены)
2.1. Полибианский квадрат (шифр Полибия)
Этот шифр относится к шифрам простой замены, в которых буквы исходного текста заменяются по определенному правилами другими буквами того же алфавита, и является возможно наиболее древним. Для шифрования используется квадратная или прямоугольная таблица, заполненная буквами алфавита в случайном порядке.
При шифровании в таблице ищется очередная буква открытого текста, а в шифротекст записывается та буква, которая расположена ниже нее в том же столбце. Если буква текста оказывается в нижней строке таблицы, то для шифротекста берут самую верхнюю букву того же столбца.
Для расшифровки обязательно необходимо знать, как был заполнен квадрат Полибия изначально. Если эта информация известна, то в нем ищется буква шифротекста и выписывается стоящая сверху нее в том же столбце. Если буква оказывается в верхней строке таблицы, то берется самая нижняя буква того же столбца.
Пример:
Необходимо зашифровать текст: «Секретные ключи.» Используем представленный ниже заполненный произвольным образом полибианский квадрат:
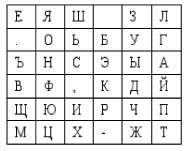
Зашифрованный текст: «,.Р-.ЛФД.БРГЦЖХЪ»
Также существует еще один вариант шифрования с использованием квадрата Полибия. При этом каждому столбцу и строке присваивается порядковый номер следующим образом:
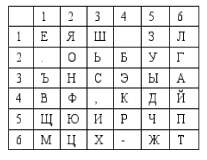
Пусть необходимо зашифровать сообщение: «Секретные ключи.» Каждая буква исходного сообщения, начиная с первой, ищется в полибианском квадрате, определяется номер строки и номер столбца, на пересечении которых она находится. Затем эти номера последовательно выписываются в шифротекст. В нашем случае зашифрованный текст будет иметь вид: «33114454116632351114441652555321»
Чтобы расшифровать полученное сообщение, как и в предыдущем случае, необходимо знать, как был изначально заполнен квадрат. Если такая информация есть, то полученная посылка разбивает на пары цифр, первая из которых — номер строки, а вторая — номер столбца, на пересечении которых в полибианском квадрате находится буква или символ зашифрованного сообщения.