Корреляционный анализ

Непрерывная автокорреляционная функция (АКФ) может быть найденная за формулой:

где непрерывный сигнал;

непрерывный сигнал с задержкой.

Рассчитаем в MathCAD коэффициенты корреляции и ковариацией относительно первого тела:

Рассчитаем автокореляційні функции для каждого из тел:

Рис.3.1 - Графики авто корреляционных функций для каждого тела

Теперь найдем взаимно корреляционные функции (ВКФ) для каждой пары сигналов.

Рис.3.2 - Графики взаимно корреляционных функций для пар сигналов

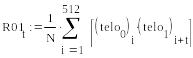
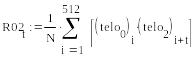
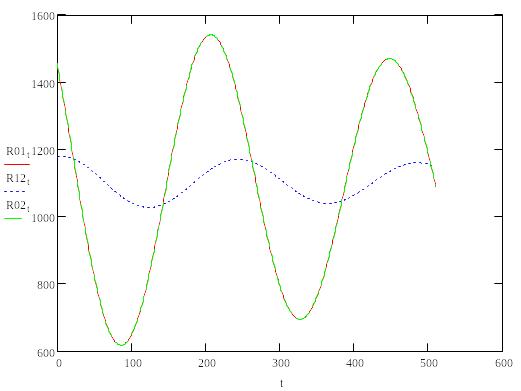
Спектральный анализ

1 Построение спектров с помощью применения дискретного преобразования Фурье:

где k=0, 1, 2, ... ,N-1.

Для первого сигнала получим:

Рис.4.1 - Спектральная характеристика, которая отвечает движению первого тела

Для второго тела:

Рис.4.2 - Спектральная характеристика, которая отвечает движению второго тела

Для третьего тела:

Рис.4.3 - Спектральная характеристика, которая отвечает движению третьего тела

2 Построение спектров с помощью применения формулы Виннера-Хинчина:

Для первого тела:

Рис.4.4 - Спектральная характеристика, которая отвечает движению первого тела

Разработка модели ацп и измерительного канала

Для измерения изменения уровня применим схему с использованием двух датчиков Д- конденсаторных уровнемеров, нормирующих устройств ЧП, которые корректируют исходный сигнал датчика для представления на АЦП, ключа К, который последовательно будет подключать каждый канал к АЦП, и сам АЦП для дальнейшей цифровой обработки сигнала.

Д1

НП1

Д2

НП2

К

АЦП

Выбор разрядности АЦП

Для выбора разрядности АЦП, используя теорему Котельникова рассчитаем частоту дискретизации сигналов на выходе системы (для расчета пользуемся пакетом MathCAD).

Для первого сигнала:

Построим спектр сигнала согласно посчитанному ограничению частоты.

Рис.5.1 - Ограниченный спектр первого сигнала

С графику видно, что в заданные границы попало 10 точек полезного сигнала. Для кодирования можно 4-воспользоваться х разрядным АЦП.

Для второго сигнала:

П остроим спектр сигнала согласно посчитанному ограничению частоты.

Рис.5.2 - Ограниченный спектр второго сигнала

Так как из анализа графику видно, что в заданных границах 10 точек, то для кодирования можно 4-воспользоваться х разрядным АЦП.

Для третьего сигнала:

Построим спектр сигнала согласно посчитанному ограничению частоты.

Рис.5.3 - Ограниченный спектр третьего сигнала

Видно, что в заданных границах 10 точек и для кодирования 4-используем х разрядный АЦП.

Из расчета видно, что для анализа всех трех сигналов можно 4-использовать х разрядный АЦП.

Проверка правильности выбора АЦП

Данная проверка базируется на установлении апертурного времени (времени установления) - времени, по окончанию которого в АЦП возникает погрешность в единицу младшего разряда при изменении сигнала по синусоидальному закону с максимально допустимой частотой.

Поскольку выбранный АЦП 4-х разрядный, то:

;

Гц.

с.

Ведь такой АЦП может иметь частоту дискретизации :

Гц.

Максимальная частота Гц, а частота дискретизации АЦП Гц, то данный АЦП способен пропускать представленные сигналы. Так как выбор АЦП правильный, используем 4- х разрядный АЦП.