2. Порядок выполнения работы

1. Войти в среду Excel. Создать новый документ, перейти на первый лист этого документа. Заполните таблицу матрицы исходов стратегий случайными числами, как показано на рисунке 5.1. Размер матрицы соответствует R=N+10, где N – порядковый номер студента по журналу. В рассматриваемом примере R равно 15;

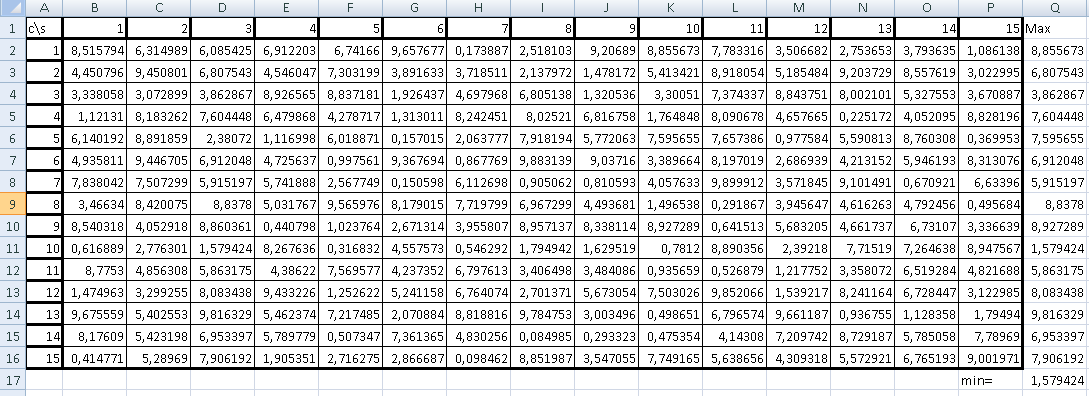
Рисунок 5.1 – Пример матрицы исходов стратегий

2. Выберите 2 стратегии природы, которые наиболее вероятны, например, 3 и 9. Рассмотрим стратегию максимина. В ячейке P1 (в столбце следующем за матрицей исходов ) записать формулу «=МАКС(C1;J1)» (для стратегии минимакса выберите функцию «МИН»). Функция «МАКС» возвращает максимальное значение из списка аргументов (функция «МИН» возвращает минимальное значение из списка аргументов);

3. В ячейках P2–P15 аналогично записать формулу «=МАКС(Cx;Jx)», где x – изменяет свои значения от 2 до 15 для соответствующих ячеек;

4. В ячейке P16 записать формулу «=МИН(P1:P15)»;

5. Исследовать полученный процесс принятия решения самостоятельно.

В случае максимина по каждой стратегии пользователя сначала определяют максимальные затраты от стратегии ВС на прогнозируемые стратегии природы и выписывают их в последней колонке. Затем выбор стратегии осуществляется по принципу минимальных затрат из максимально возможных.

Во втором случае по каждой стратегии пользователя на прогнозируемые стратегии природы сначала определяют минимальные экономии от стратегии и выписывают их в последней колонке. Затем выбор стратегии осуществляется по принципу максимальной экономии из минимально возможных вариантов.

3. Варианты заданий

1. Построить программную модель матрицы всех возможных исходов стратегий по виду таблицы матрицы исходов стратегий. Размер матрицы соответствует R=N+10, где N – порядковый номер студента по журналу;

2. С использованием генератора случайных чисел (ГСЧ) заполнить матрицу значениями экономии от применения стратегии ВС e_ij (для нечетных вариантов) и затрат z_ij (для четных вариантов). Диапазон изменения значений 1-10;

3. C использованием ГСЧ выбрать два номера наиболее вероятных случайных стратегий природы из диапазона 1-R, например 5 и 10 (в общем случае число наиболее вероятных стратегий может быть любым из диапазона 1-R);

4. Для данных стратегий природы по принципу минимакса для нечетных вариантов и максимина – для четных вариантов выбрать оптимальную стратегию ВС;

5. Сравнить эффективность выбранной стратегии ВС с другими стратегиями ВС для конкретной стратегии природы. Для этого распечатать таблицу;

6. Сделать выводы по работе.

3. Контрольные вопросы

1. Изложить принцип Эшби.

2. Объясните стратегии минимакса и максимина.

3. Привести примеры программных средств, которые позволяют моделировать системы принятия решений.

4. Привести примеры аппаратно-программных средств, которые позволяют моделировать системы принятия решений.

6 Лабораторная работа №6. Оптимизация топологии распределенной системы

Цель работы: изучить синергетический алгоритм оптимизации топологии распределенной системы контроля и управления