Система незалежних регресій.

Означення 10. Економетрична модель називається системою незалежних регресій, якщо кожне з регресійних рівнянь, яке входить до системи має тільки одну залежну ендогенну змінну, яка не залежить від ендогенних змінних інших рівнянь і не впливає на інші ендогенні змінні.

У загальному випадку система k незалежних рівнянь має вигляд:

( 25 )

Як бачимо, до кожного окремого рівняння системи можна застосувати 1 МНК і знайти оцінки параметрів цього рівняння. Прикладом такої моделі є модель формування рівноважної ціни на ринку, яка складається з наступних двох рівнянь :

Функція попиту ( 26 )

Функція пропозиції ( 27 )

де х – ціна ,y₁ – попит, y₂ - пропозиція.

Означення 11. Економетрична модель називається рекурсивною, якщо її структурні рівняння можна впорядкувати таким чином, щоб перше містило у правій частині тільки екзогенні змінні, друге – екзогенні змінні і першу ендогенну, третє – екзогенні змінні, а також першу і другу ендогенні змінні і так далі.

У загальному випадку рекурсивну модель можна представити наступним чином :

( 28 )

Особливістю рекурсивних моделей є те, що матриця А при ендогенних змінних у правій частині рівнянь системи представляє собою трикутну матрицю, головна діагональ якої містить одиниці, а елементи під головною діагоналлю дорівнюють нулю.

Оцінювання параметрів моделі представляє собою рекурсивну процедуру (звідси і назва моделі). Спочатку на основі 1МНК оцінюють параметри першого рівня системи. Потім застосовуючи обчислене 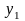, як пояснюючу змінну, оцінюються параметри другого рівняння і т. д.

А. Підхід Койка.

Для оцінювання параметрів дистрибутивно-лагових моделей Койк ввів припущення, що коефіцієнти лагу маючи той самий знак зменшуються у геометричній прогресії:

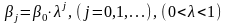, ( 9 )

де - темп зменшення дистрибутивного лагу: (1 - ) – швидкість пристосування залежної змінної.

Вираз (9) показує, що кожний наступний коефіцієнт менший, ніж попередній, тобто з кожним наступним кроком у минуле вплив часового лагу на залежну змінну поступово зменшується, що є досить логічним і ймовірним припущенням стосовно багатьох економічних явищ і процесів.

Використовуючи вираз (9) модель (1) можна перетворити у наступну:

. ( 10 )

Параметри рівняння (10) можна оцінити методами нелінійного регресійного аналізу, які є достатньо складними і об’ємними, хоча використання ПЕОМ не створює ніяких обчислювальних проблем. Однак більш розповсюдженою і ефективною є схема обчислень на основі перетворення Койка. Суть цього перетворення полягає у наступному. Запишемо вираз (10) для моменту часу і помножимо ліву і праву частину його на . Тоді будемо мати:

. ( 11 )

Віднявши (11) від (10) отримаємо:

, ( 12 )

де 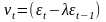- ковзаюче середнє між і . Перетворення моделі (1) в (12) називається перетворенням Койка.

Модель (12) дозволяє аналізувати як короткострокові так і довготривалі властивості змінних. У короткостроковому періоді параметр є короткостроковим мультиплікатором, у довгостроковому періоді – довгостроковим мультиплікатором є вираз .

Перетворення Койка мають наступні позитивні наслідки:

1. модель незкінченого розподіленого лагу (1) перетворюється на авто регресійну тільки з трьома невідомими параметрами: і ;

2. знімається проблема мультиколінеарності.

Але при застосуванні перетворення Койка можливі наступні проблеми.

1. Серед пояснюючих змінних у правій частині (12) з’являється стохастична змінна , що порушує одне з припущень про не стохастичний характер факторів. Крім цього потрібно тепер перевірити припущення класичного лінійного регресійного аналізу щодо незалежності розподілу від випадкової величини.

2. Якщо для випадкових величин і вихідної моделі (1) і виконується припущення 1 МНК про відсутність авто кореляції залишків, то для випадкової величини , вочевидь має місце серійна автокореляція залишків. Оскільки наявність у правій частині рівняння (12) лагового значення залежної змінної порушує одну з умов d – тесту Дарбіна – Уотсона для тестування автокореляції залишків в таких моделях необхідно застосувати інші тести.

 Зауваження 3. Модель Койка фактично є послідовною моделлю, оскільки її можна одержати чисто математичним шляхом . Внаслідок цього вона позбавлена будь-якого теоретичного обґрунтування. Але цей розрив можна подолати розглядаючи наступні дві моделі : модель адаптивних очікувань і модель часткового коригування