2.1. Определение приведённых факторов

Выбираем схему динамической модели с распределёнными факторами.

В качестве звена приведения выбираем кривошип (рис. 6):

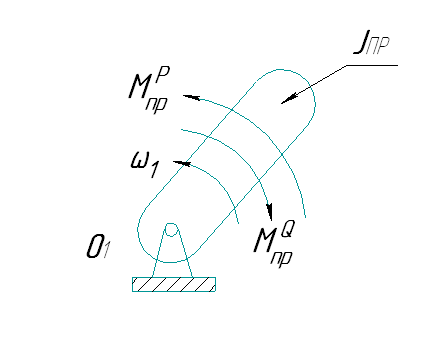
где ω₁ – угловая скорость звена приведения;

J_пр – приведённый момент инерции кривошипа;

, - приведённые моменты движущих сил и сил сопротивления.

Рис. 6 Динамическая модель

Используя результаты кинематического анализа, рассчитываем J_пр и

для исследуемого положения механизма. Учитывая, что V_S3 =0, G₄ =0, J_S4 =0,

записываем выражение для J_пр :

Выражение для запишется в виде:

Учитывая, что VS3 =0, VS5 =VC5 =V5 , G4 =0, получим:

2.2. Построение диаграмм

1. По результатам компьютерного расчета для 12-ти положений строим график изменения приведенного момента сил сопротивления в зависимости от угла поворота кривошипа = f(φ) (см лист 2). Масштабные коэффициенты и задаем согласно рекомендациям по выполнению курсового проекта:

2. Методом графического интегрирования графика = f(φ) получаем график

работы приведенных сил сопротивления = f(φ) . Базу интегрирования Н_F

принимаем равной 70 мм.

Масштабный коэффициент работы (кинетической энергии) рассчитываем

по формуле:

= = Н · · = 70· 0,035· 6 = 14,7 Dж/мм;

3. График работ движущих сил = f(φ) строится из условия равенства нулю

изменения кинетической энергии за полный цикл периодически установившегося

режима работы механизма: Δ = + = 0, а также принятого допущения:

= const. Из формулы следует, что = – ;

Строим графики работ движущих сил в отрицательной и положительной

области.

4. График изменения кинетической энергии Δ = f(φ) внутри цикла строится

как алгебраическая сумма работ сил движущих и сил сопротивления для

каждого положения механизма: Δ = +

5. По результатам компьютерного расчета для 12-ти положений механизма

строим график изменения приведенного момента инерции в зависимости от угла

поворота кривошипа J_пр= f(φ); задаем масштабный коэффициент приведенного

момента инерции :

Для удобства дальнейших построений ось углов на графике располагаем

вертикально, а ось приведенных моментов инерции располагаем горизонтально.

6. Диаграмму энергомасс Δ = f( ) строим методом графического исключения параметра φ из графиков Δ = f(φ) и = f(φ);

2.3. Определение момента инерции маховика и его размеров

Используя диаграмму энергомасс, определяем момент инерции маховика.

1. По формулам рассчитываем углы и :

2. Под найденными углами проводим касательные к диаграмме энергомасс

(соответственно сверху и снизу);

3. Замеряем в мм отрезок ab, который касательные отсекают на вертикаль-

ной оси диаграммы;

4. Рассчитываем требуемую величину момента инерции маховика сни-

жающего колебания угловой скорости до заданного уровня:

5. Рассчитываем геометрические размеры маховика:

h = 0,2 = 0,2 · 1,17=0,234 ;

b = 0.1 = 0,1 · 1,17=0,117 ;

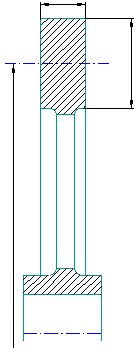
Рис. 7 Эскиз маховика