Скорости точек механизма

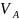
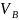
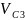
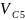
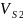
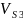
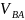
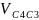
м/с	м/с	м/с	м/с	м/с	м/с	м/с	м/с	м/с	ω1 1/с	ω2 1/с	ω3 1/с	ω4 1/с
5,57	6,3	3,92	3,99	0	5,25	0	5,6	0,63	-14,65	3,52	5,63	5,63

Знак «–» означает, что угловая скорость звена направлена по ходу часовой

стрелки

1.5.2. Построение плана ускорений

А) механизм I класса (звено 1вместе со стойкой).

Точка А кривошипа О₁А совершает вращательное движение вокруг точки О₁, поэтому её ускорение есть сумма нормального и касательного ускорений:

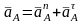
Поскольку принято n₁=сonst (следовательно, ε₁ = 0), то

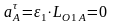
Модуль ускорения

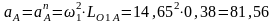м/с²

На плане ускорений этот вектор изображается отрезком 136 мм, направленным от точки А к О₁. Масштаб плана ускорений:

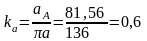м/с²∙мм

Б) группа Ассура II₁ (2,3)

Составляется система векторных уравнений, связывающих ускорение внутренней точки В с ускорениями внешних точек А и О₃ :

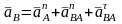
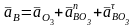
В этой системе модули нормальных ускорений определяются по формулам:

aⁿ_BA = ω₂² ∙L_AB = (3,52)² ∙1,59 = 19,7 м/с²

aⁿ_BO3 = ω₃² ∙L_BO3 = (5,63)² ∙1,12 = 35,5 м/с²

Чтобы эти ускорения изобразить на плане ускорений, разделим полученные значения на масштаб плана ускорений и получим длины отрезков в мм:

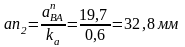
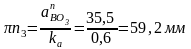
Согласно векторным уравнениям строим план ускорений: из полюса плана (точка π) проводим отрезок πа длиной 136 мм, направлен-

ный к центру вращения кривошипа, параллельно направлению кривошипа в

9-м положении. Из точки а проводим отрезок an₂ в направлении, параллельном звену АВ механизма. Из полюса π (с ним совпадают все неподвижные

точки механизма: О₁, S₁, О₃, S₃) откладываем отрезок πn₃ , параллельный

звену ВD; через конец вектора an₂ проводим отрезок произвольной длины,

перпендикулярный звену АВ, а через конец вектора πn₃ проводим отрезок произвольной длины, перпендикулярный звену ВD. Точка пересечения перпендику-ляров АВ и ВD есть точка b (смотри лист 1). Отрезок n₂b на плане соответствует касательному ускорению 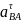, а отрезок n₃b на плане соответствует

касательному ускорению

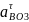
Чтобы определить величину ускорения точки по плану ускорений, нужно

соответствующий отрезок на плане измерить в мм и умножить эту величи-

ну на масштабный коэффициент ускорений:

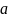_B = (πb) ∙ K_а = 85 ∙0,6 = 51 м/с²

= (n₂b) ∙ K_а = 142 ∙0,6 = 85,2 м/с²

= (n₃b) ∙ K_а = 60 ∙0,6 = 36 м/с²

Ускорения точек S₂ и С₃ определяем с помощью теоремы подобия, на основании которой составляем пропорцию, связывающую чертёжные (или истинные) размеры звена 2 (АВ, АS₂) с отрезками плана ускорений:

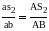
Из уравнения определяем длину неизвестного отрезка:

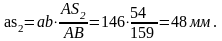
Отрезок аs₂ откладываем от точки а на плане ускорений по линии ab. Точка s₂ является концом вектора _S2, начало всех векторов – в полюсе π. Поэтому отрезок πs₂ на плане ускорений изображает вектор _S2 :

_S2 = (πs₂) ∙ K_а = 100 ∙0,6 = 60 м/с²

Ускорение точки С₃ определяем аналогично по принадлежности звену 3:

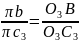
Из формулы определяем длину неизвестного отрезка:

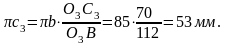
Этот отрезок откладываем от полюса π на плане ускорений в сторону, противоположную отрезку πb (см план ускорений на листе 1).

Модуль вектора ускорения _С3 определяем по формуле:

_С3 = (πc₃) ∙K_а =53 ∙ 0,6= 31,8 м/с²

Определяем величины угловых ускорений звеньев 2 и 3:

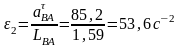
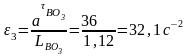
Для определения направления ε₂ отрезок n₂b на плане ускорений устанавливается в точку В, а точка А закрепляется неподвижно. Тогда становится очевидным, что ε₂ направлено по часовой стрелке. Для определения направления ε₃ отрезок n₃b устанавливается в точку В, точка О₃ неподвижна. Следовательно, ε₃ направлено против часовой стрелки (см рис. 5)

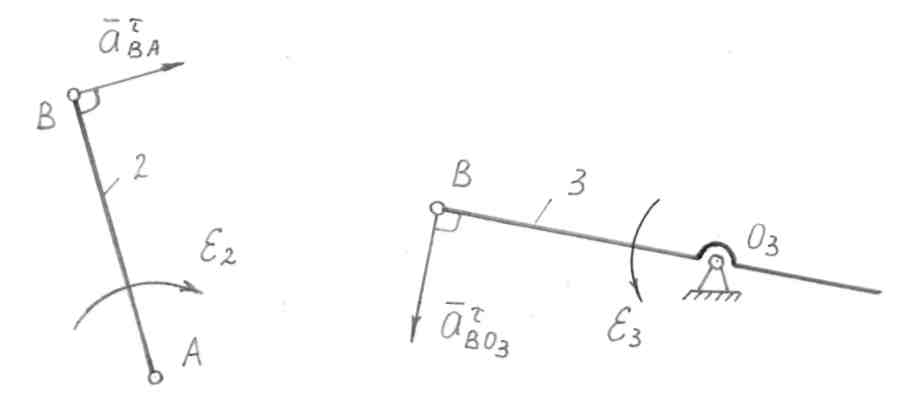
Рис. 5 Определение направлений угловых ускорений звеньев

В) Группа Ассура II₄ (4,5)

Так как группа Ассура, состоящая из звеньев 4 и 5 относится к 4-му виду

(в состав группы входят две внешние поступательные и одна внутренняя

вращательная кинематическая пара, см рис. 3), то векторные уравнения для

определения ускорения 5-го звена запишутся в виде:

а_С4(5) = а_C3 + а_кор + а_C4С3

а_С5 = а_NN + а_C5,NN

где а_С4(5) – ускорение шарнира С, который соединяет 4-е и 5-е звенья;

а_C3 – ускорение полюса С₃, лежащего на кулисе BD;

а_кор – ускорение Кориолиса, вектор а_кор направлен перпендикулярно кулисе BD;

а_C4С3 – ускорение точки С, принадлежащей ползуну 4, в ее поступательном

движении относительно точки С₃ на кулисе; вектор а_С4(5) направлен

параллельно кулисе BD;

а_С5 – ускорение точки С, принадлежащей 5-му звену;

а_NN – ускорение неподвижных направляющих, по которым перемещается

5-е звено (а_NN =0);

а_C5,NN – ускорение точки С, принадлежащей 5-му звену, которое определено в

поступательном движении относительно неподвижных направляющих NN;

вектор а_C5,NN направлен параллельно направляющим NN;

Ускорение Кориолиса вычислим по формуле:

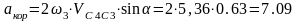м/с²

Разделив найденное значение а_кор на масштабный коэффициент ускорений, получим длину отрезка в мм, которым вектор ускорения Кориолиса изобразится на плане ускорений:

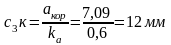
Откладываем на плане ускорений данный отрезок от точки С₃ в направлении, перпендикулярном кулисе BD, согласно правилу Жуковского; через точку К проводим отрезок произвольной длины, параллельный кулисе BD; через точку π

(полюс плана) проводим отрезок произвольной длины, параллельный направляющим NN; точка пересечения этих отрезков есть точка С₅ (см план ускорений на листе 1).

Модули векторов ускорений _С5 и а_C4С3 определяем по формулам:

_С5 = (πc₅) ∙K_а = 25∙0,6 = 15 м/с²

а_C4С3 =(кc₅) ∙ K_а = 33∙0,6 = 19,8 м/с²

Так как ползун 4 поворачивается вместе с кулисой BD, его угловое ускорение

по величине и по направлению равно угловому ускорению кулисы BD:

𝛆₄ = 𝛆₃

Величины ускорений, определенные по плану, занесем в таблицу.

Таблица 1.4