9.3. Задачи в условиях неопределенности
Наиболее характерным типом задач разработки инновационных решений являются задачи в условиях неопределенности. Для этих задач характерна большая неполнота и недостоверность информации, многообразие и сложность влияния социальных, экономических, политических, технических и других факторов. Эти обстоятельства не позволяют построить адекватные математические модели решения задач по определению оптимального решения. В таких случаях для определения наилучших решений используются следующие критерии:
критерий гарантированного результата (максиминный критерий Вальда) – это пессимистический по своей сути критерий, поскольку принимается во внимание только безопасный из всех возможных результатов каждой альтернативы. Данный принцип заключается в выборе в качестве оптимальной той альтернативы (стратегии), которая имеет наибольшее среди наименее благоприятных состояний внешней среды значение функции полезности;
критерий оптимизма (критерий максимакса) предполагает возможность получения максимального уровня желательности результата. Он также относится к разряду осторожных критериев, при этом допускается, что результаты выбираются разумным противником, интересы которого прямо противоположны, то есть предполагается следующее: если применяемые правила принятия решений позволяют противнику извлечь какое-либо преимущество, то он обязательно это сделает. Однако если исключить вполне определенные условия конкурентной борьбы, то столь пессимистические допущения нельзя оправдать, поскольку результаты могут выбираться нерациональным «противником», а цели «противника» не обязательно полностью противоречат целям конкурента;
критерий Лапласа применяется, если состояния внешней среды неизвестны, но их можно считать равновероятными;
критерий обобщённого максимина или критерий Гурвица представляет собой комбинацию принципа гарантированного результата и принципа оптимизма, позволяет учитывать состояние между крайним пессимизмом и безудержным оптимизмом;
критерий минимаксного риска Сэвиджа рассматривается как критерий наименьшего вреда, который характеризует те потенциальные потери, которые понесёт фирма, если выберет неоптимальное решение.
Основную роль в поиске оптимального или приемлемого решения выполняет лицо, принимающее решение (ЛПР).
ЛПР, перед которым возникла задача, представленная в таблице 7, может рассуждать следующим образом: при выборе С минимальный возможный выигрыш равен 1; при выборе С – равен 2. Следовательно, целесообразно выбрать С, поскольку эта стратегия максимизирует минимальный выигрыш.
Критерий максимина используемый при таком подходе, определяется следующим образом:
max
min
,
где – полезность, полученная ЛПР при достижении результата , с помощью стратегии в соответствующих внешних условиях.
Это своего рода критерий для осторожного человека. Им главным образом следует пользоваться в тех случаях, когда действия направлены на удовлетворение жизненно важных потребностей и необходимо обеспечить успех при любых возможных условиях.
Предположим,
что результат мог бы выбираться лицом,
являющимся противником (конкурентом)
первого лица. При этом противник платит
за те блага, которые получены первым
лицом. Противник мог бы рассуждать так:
при выборе
максимальные возможные потери равны
2; при выборе
– равны 5.
Таким образом, целесообразно выбрать , поскольку этот результат минимизирует максимальные потери (минимакс):
max min .
Критерий Гурвица имеет вид:
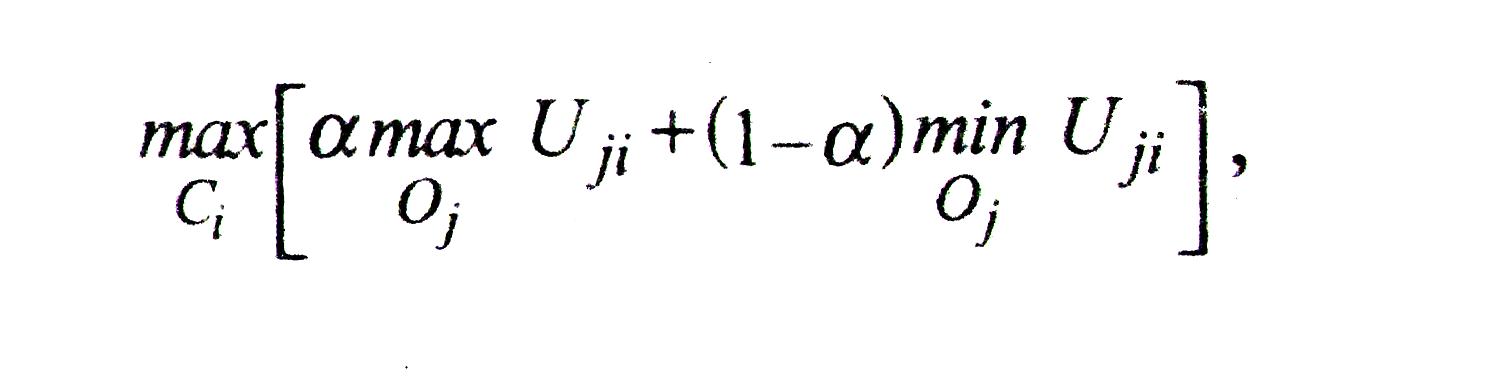
где 0≤α≤1.
Величину
α можно рассматривать как показатель
оптимизма. Если α=0, то критерий Гурвица
сводится к максимину. С другой стороны,
если α=1, то критерий становится
максимаксом, то есть он будет непосредственно
приводить к выбору такой стратегии,
которая максимизирует максимальный
выигрыш. Это самый оптимистический
критерий. Предположим, что α принимается
равной 0,6 и применяется платежная матрица
(см. табл. 7). Тогда если ЛПР выбирает
стратегию
,
то максимальный выигрыш равен 5, а
минимальный – 1. Следовательно,
0,6×5+0,4×1=3,4.
Аналогично,
если он выбирает
,
то 0,6×3+0,4×2=2,6.
По этому критерию оптимальной стратегией является С1 субъективную оценку вероятности, то критерий Гурвица эквивалентен максимизации ожидаемой полезности.
Для применения критерия минимаксного сожаления платежную матрицу необходимо преобразовать в матрицу потерь. В каждую клетку такой матрицы записывается разность между максимально возможным результатом и результатом, получаемым при реализации определенной стратегии. Так, например, платежная матрица преобразуется в матрицу потерь (табл. 4).
Если ЛПР выберет стратегию , то потери на первом результате составят 2-1=1; на втором результате потерь не будет. Если руководитель выберет стратегию , то потерь на первом результате не будет, а на втором они составят 5-3=2. Матрица потерь отражает потери для случая, когда фактический выбор стратегии не является наилучшим, сточки зрения достижения одного из возможных результатов.
Таблица 4
Матрица потерь
|
|
|
|
|
|
|
1 |
0 |
|
0 |
2 |
После построения матрицы потерь к ней можно применить минимаксный критерий для отбора оптимальной стратегии; такой стратегией в данном случае является первая.
Критерий минимаксного сожаления также относится к категории осторожных. Однако, если, руководствуясь минимаксным критерием, ЛПР прежде всего думает о том, как меньше потерять, то при использовании второго критерия он придает выигрышу несколько большее значение, нежели потерям.
Для выбора оптимальной стратегии с помощью критерия Лапласа оценка каждой j-й стратегии производится как среднее арифметическое в j-й строке:
Наиболее
предпочтительным считается вариант
действий, которому соответствует
максимальное значение U
.
Попытка сформулировать критерий оценки возможных решений в условиях неопределенности отражает стремление сделать более наглядными преимущества и недостатки каждого варианта действий в различной обстановке.
При сравнительном анализе критериев эффективности нецелесообразно останавливаться на выборе единственного критерия. Поскольку это может привести к неоправданным решениям, ведущим к значительным потерям. Поэтому имеется необходимость применения нескольких критериев в совокупности.
На практике часто используются подходы, в которых нашли широкое применение многокритериальные оценки эффективности различных вариантов решений, не сводящиеся к чисто математической постановке задачи, когда в качестве одного из оценочных критериев используется вероятность достижения запланированных результатов. Широкое распространение получил графоматематический метод, названный «дерево решений», в основе которого лежит динамическое программирование и теория статистических решений.
Например, руководство должно решить: строить большой или маленький завод для производства нового вида продукции, потребность в котором точно не установлена.
Таким решениям должно предшествовать изучение потребности (спроса) в продукции, выпуск которой планируется. Изменение спроса, как правило, носит вероятностный характер. Расчет вероятности возникновения определенных величин спроса с учетом влияния некоторых факторов на изменения потребности производится с помощью вероятностного графа изменения потребности (рис. 12).
Вероятностный граф позволяет наглядно представить все возможные варианты развития потребности в планируемой продукции, дать количественную оценку вероятности появления этих вариантов (в данном случае выявлено четыре варианта).
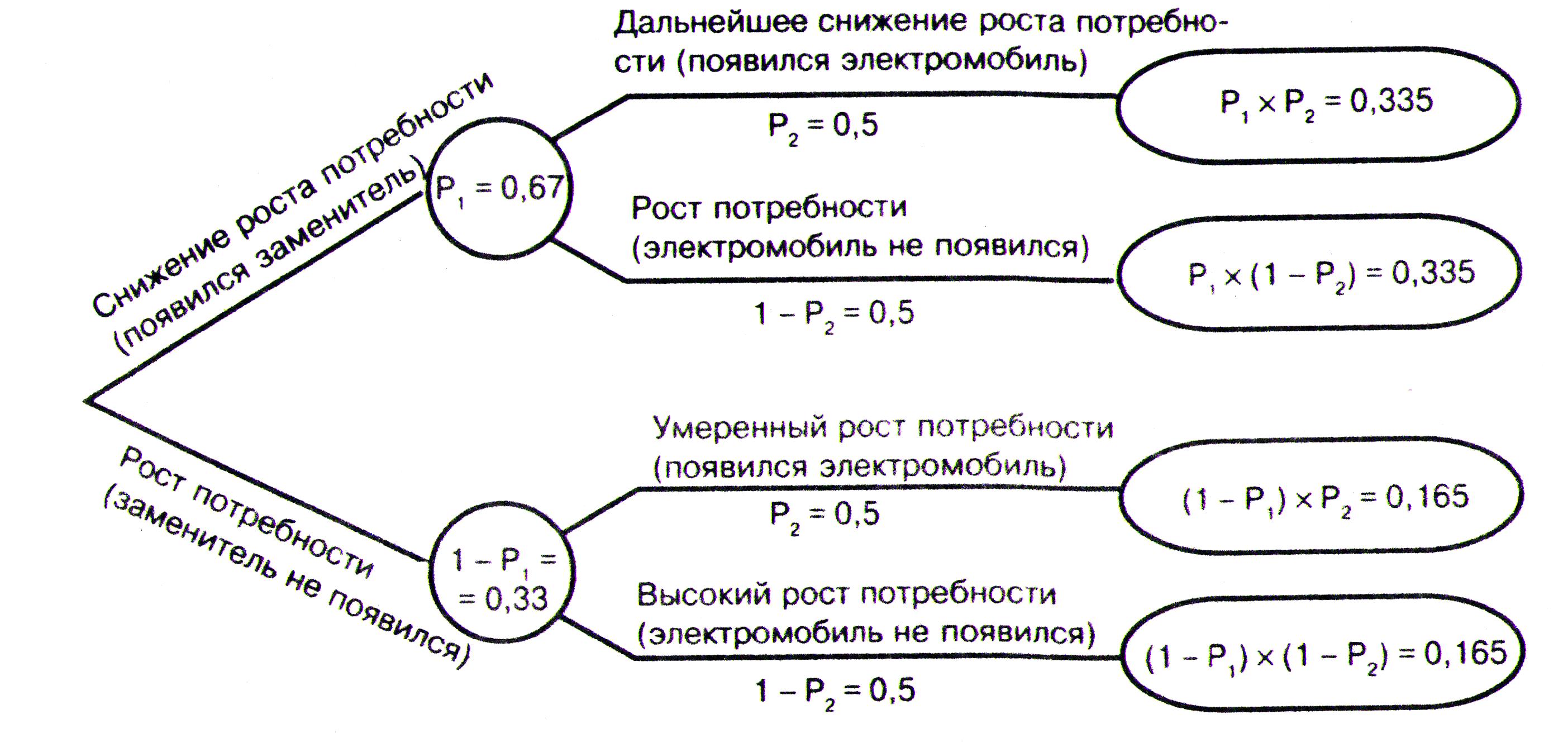
Рис. 12. Вероятностный граф изменения потребности
В рассматриваемом примере, возможно, спрос на продукцию будет высоким в течение первых двух лет ее выпуска, а в дальнейшем потребители найдут ее неудовлетворительной и спрос упадет (рассматривается 10-летний период работы завода.). Но может быть, начальный высокий спрос на продукцию сохранится и в дальнейшем.
В том случае, когда начальный спрос на продукцию высок, а построен завод небольших размеров, можно спустя два года после начала работы завода его расширить.
На рис. 14 приводится «дерево решений» рассматриваемой проблемы.
Ветви дерева отображают различные события, которые могут иметь место, а его узлы (вершины) – состояния, в которых возникает необходимость выбора. В узлах-квадратах выбор из некоторого набора альтернатив осуществляет руководство отрасли; а в узлах кружках выбор решения производит «природа», а руководство отрасли может лишь оценить вероятность того или иного выбора «природы» (различного опроса на продукцию завода). Для принятия обоснованного решения нужны количественные данные.
Предположим, что в результате оценки спроса на продукцию удалось определить следующие его уровни и вероятности их реализации (табл. 5).
Таблица 5
Уровень спроса и вероятность его реализации
Уровень спроса |
Вероятность |
Высокий вначале спрос остается высоким и в дальнейшем |
0,6 |
Высокий вначале спрос в дальнейшем будет низким |
0,1 |
Низкий вначале спрос и в дальнейшем будет низким |
0,3 |
Низкий вначале спрос в дальнейшем будет высоким |
0,0 |
Вероятность первоначально (в течение первых двух лет) высокого спроса на продукцию составляет 0,7 (0,6+0,1). Если спрос останется высоким и в оставшиеся 8 лет, то вероятность этого события равна 0,86 (0,6/0,7) и соответственно вероятность низкого последующего спроса составит 0,14 (0,1/0,7).
Были произведены также оценки возможного дохода. Все данные приводятся на дереве решений (рис. 14).
Метод дерева решений реализуется в такой последовательности:
строится временной граф процесса принятия решений и возможных альтернатив развития экономического объекта, возникающих в результате осуществления тех или иных решений;
определяются точки принятия решений по реализации той или иной из числа существующих альтернатив;
находятся точки, где существует неопределенность (выбор решения производит «природа», и вид или диапазон альтернативных результатов в этих точках;
оценивается вероятность различных событий или результатов действий, затраты ресурсов и экономический эффект, получаемые в результате реализации различных стратегий;
выбираются наилучшие альтернативные варианты решений.
Применение этого метода дает возможность при принятии решений представить известные данные в виде, удобном для анализа.
Анализируя дерево решений и проводя расчеты, ЛПР двигается от конечного решения к начальному, последовательно выбирая оптимальные в каждой точке.
Две возможные альтернативы в точке 2 (рис. 13) сравниваются с помощью расчетов (табл. 6).
Согласно таблицы 6 завод необходимо расширять, следовательно, из рассмотрения исключается один из существующих альтернативных вариантов в точке 2. Для выбора лучшего варианта решения в точке 1 производятся следующие расчеты.
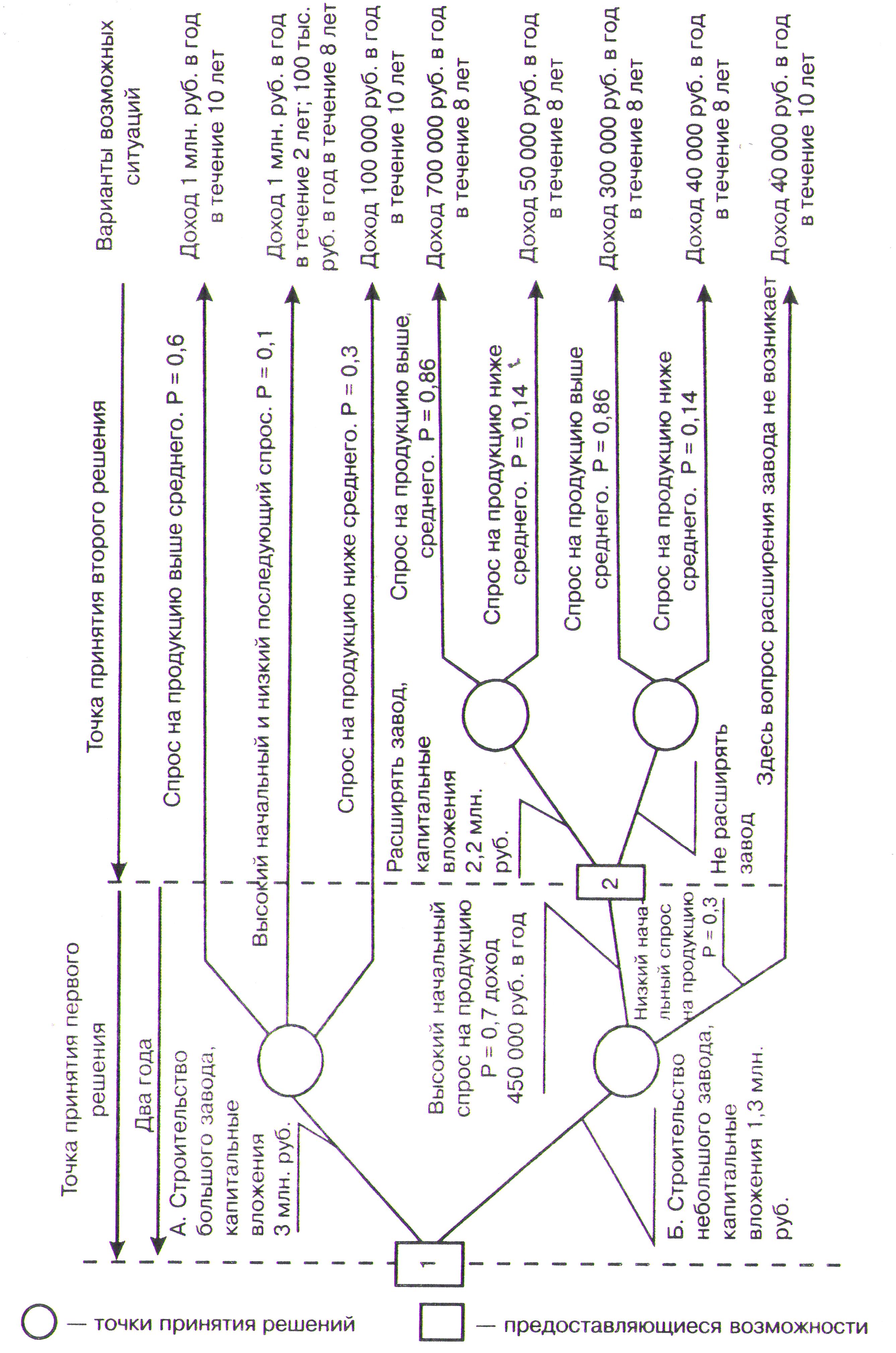Рис. 13.
«Дерево решений»
Таблица 6
Параметры альтернатив в точке 2
Альтернатива |
Условия спроса |
Вероятность |
Суммарный доход, млн руб. |
Ожидаемый доход и чистый доход, млн руб. |
Расширение завода |
Спрос выше среднего |
0,86 |
0,7×8=5,6 |
5,6×0,86=4,816 |
Спрос ниже среднего |
0,14 |
0,05×8=0,4 |
0,4×0,14=0,056 4,872-2,2=2,672 |
|
Прежний размер завода |
Спрос выше среднего |
0,86
|
0,3×8=2,4 |
2,4×0,86=2,064 |
Спрос ниже среднего |
0,14 |
0,04×8=0,3 |
0,32×0,14=0,0448 2,1088-0,0=2,1088 |
Строительство большого завода принесет следующий чистый доход:
{(10 млн. руб.×0,6)+[(1 млн. руб.×2)+(0,1 млн. руб.×8)]×0,1+(0,1 млн. руб.×10) ×0,3}-3 млн. руб.=3,6 млн. руб.
Строительство малого завода принесет следующий чистый доход:
{(2,672 млн. руб. + (0,45 млн. руб.×2)]×0,7+(0,04 млн. руб.×10) ×0,3}-1,3 млн. руб.=1,340 млн. руб.
Следовательно, нужно строить большой завод. Для упрощения в примере не учитывается фактор дисконтирования и время, необходимое для строительства и реконструкции заводов.
Принципы, лежащие в основе метода дерева решений, сводятся к следующему.
1. Эффективность решения (цена) в любом узле, где выбор производит «природа», зависит только от будущих событий и не зависит от ранее принятых решений.
2. В любом узле, где решение принимает руководитель, выбор заключается в переходе к наиболее «прибыльному», непосредственно следующему за ним узлу, а цена такого узла определяется ценой последующего за вычетом затрат на переход в последующий узел.
3. С учетом пунктов 1 и 2 можно оценить всю систему и найти оптимальные решения, производя вычисления против течения времени.