1. Производная по направлению.

Пусть в области задано скалярное поле u u(x;y;z) и задан трехмерный вектор . Рассмотрим некоторую фиксированную точку P₀(х₀;у₀;z₀) 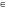D и точку P (x;y;z) D с текущими координатами, но такую, чтобы 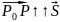. Обозначим u 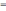u(P) – u(P₀) – приращение функции u в точке P₀ по направлению вектора .

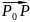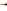Определение 1. Производной функции u u(x;y;z) в точке P₀(х₀;у₀;z₀) по направлению вектора называется предел отношения приращения u u(P) – u(P₀) к расстоянию | | при условиях, что P P₀( ) и этот предел существует. Обозначение:

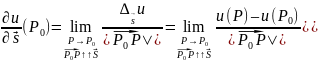
Теорема. Пусть функция u u(x;y;z) дифференцируема в точке P₀(х₀;у₀;z₀). Тогда в точке P₀ существует производная функции u по направлению вектора и справедливо равенство:

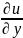(P₀) (P₀) + (P₀) + (P₀) ,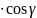

где , ,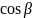 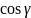- направляющие косинусы вектора .

Доказательство.

Возьмем точку P (x₀ + ; y₀ + ; z₀ + z) так, чтобы .

Так как функция u(x;y;z) дифференцируема в точке P₀, то:

u u(P) – u(P₀) (P₀) + (P₀)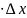 + 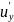(P₀) + , где

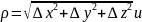
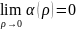
Так как , то углы 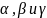, которые составляет вектор с осями координат Ох, Оу и Оz соответственно, такие же для вектора

Поэтому: , ,

, , .

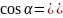
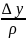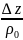
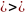
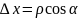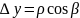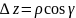Тогда u (P₀)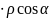 + (P₀) + (P₀) + .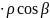

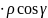(P₀) + (P₀) + (P₀) + .

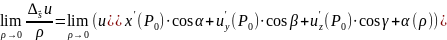
(P₀)

(P₀) . Ч. Т. Д.

Рассмотрим частные случаи производной по координатным направлениям.

1. Пусть =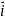 , тогда

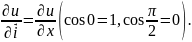
2. Пусть = 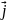, тогда .

3. Пусть = , тогда .

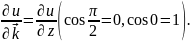
БИЛЕТ№34

2. Градиент и его свойства.

Пусть в области D R³ задано скалярное поле u u(x;y;z) и в каждой точке области D функция u(x;y;z) дифференцируема.

Определение 2. Градиентом функции u(x;y;z) в точке P₀(х₀;у₀;z₀) D называется вектор, координатами которого являются значения частных производных функции u(x;y;z) в этой точке:

Свойства вектора градиента.

Свойство 1. Производная функции 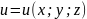в точке 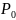по направлению вектора равна скалярному произведению вектора градиента этой функции в точке на единичный вектор :

Свойство 1 следует из формулы скалярного произведения векторов и определения вектора градиента.

Свойство 2. Производная функции в точке по направлению вектора равна проекции вектора на вектор :

Свойство 2 следует из свойства 1, определения скалярного произведения и определения проекции вектора на ось.

Свойство 3. Производная функции в точке по направлению вектора градиента функции в точке равна длине вектора :

=

Свойство 3 следует из формулы производной по направлению вектора с учетом того, что направляющие косинусы вектора =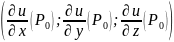 вычисляются по формулам:

;

;

.

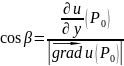Свойство 4. Производная функции в точке по направлению вектора принимает наибольшее значение по сравнению с производными от этой функции в точке по любому другому направлению.

Действительно, из свойства 2: = , но если , то угол

Следовательно, ,

то есть равен своему максимальному значению.

Свойство 5. Вектор направлен по нормали к поверхности уровня 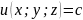, где .

Следствие из свойств вектора .

Градиент функции в каждой точке направлен в сторону наибольшего роста функции , причем скорость изменения функции в этом направлении равна длине вектора .

Пример. Найти величину и направление наибольшего роста функции в точке .

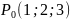Решение. Учитывая сформулированное следствие из свойств вектора , найдем .

; ; .

; ; .

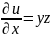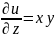Следовательно:

.

Ответ: величина наибольшего роста функции в точке равна 7;

направление наибольшего роста функции в точке определяется вектором , или его направляющими косинусами :

БИЛЕТ№35