2. Монотонность функции

Определение 4. Функция y = f(x) называется возрастающей (убывающей) на промежутке (a;b), если для любых x₁ и x₂, принадлежащих этому промежутку, из условия x₂ > x₁ следует неравенство:

f(x₂) > f(x₁) (f(x₂) < f(x₁)).

Определение 5. Функция y = f(x) называется монотонной на промежутке (a;b), если она на этом промежутке является только возрастающей или только убывающей.

Теорема 2 (достаточные условия монотонности).

Если функция y = f(x) дифференцируема на промежутке (a;b) и f’(x) > 0 (f’(x) < 0) для любых x  (a;b), то функция возрастает (убывает) на этом промежутке.

Необходимые условия

Если функция y = f(x) дифференцируема на промежутке (a;b) и f’(x) ≥0 (f’(x) ≤ 0) для любых x  (a;b), то функция возрастает (убывает) на этом промежутке.

БИЛЕТ№14

3. Экстремумы функции

Определение 6. Функция y=f(x) x₀Î D(f) максимум y_max (минимум y_min), если существует такая, окрестность точки x₀, для всех x из которой выполняется неравенство:

f(x₀) > f(x)  (f(x₀) < f(x)).

Определение 7. Точки максимума и минимума функции называются точками экстремума функции.

Теорема 3 (необходимое условие экстремума)

Если функция y = f(x) имеет экстремум в точке x₀, то в этой точке производная функции равна нулю или не существует.

Доказательство.

1) Для определенности рассмотрим случаи, когда функция y = f(x) в точке x₀ имеет максимум и в этой точке существует производная. Тогда из определения максимума для любого x, принадлежащего окрестности точки x₀ f(x₀) > f(x).

Отсюда следует, что для любого x  0 справедливо неравенство: f(x₀+x) - f(x₀) < 0. Разделим неравенство на Dx. При этом получим:

при Dx > 0:

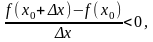
при Dx < 0:

Перейдем к пределам:

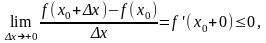
Так как f”(x₀) существует, то:

f’(x₀+0) = f’(x₀-0) = f(x₀) = 0.

Аналогично рассматривается случай, когда x₀ – точка минимума.

2) Если f' (x₀) не существует или равна ¥, то точка x₀ может быть точкой экстремума функции.

Например, функция y = 1х1 имеет минимум при x = 0, хотя y' (0) не существует (рис.9)

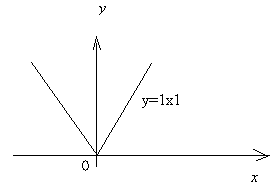
Рис. 9

Теорема доказана.

Теорема 4 (достаточное условие экстремума)

Если функция y = f(x) непрерывна в точке x₀, дифференцируема в некоторой ее окрестности за исключением, может быть, самой этой точки, f’(x₀) = 0 или не существует и при переходе x через точку x₀ f’(x) изменяет знак, то точка x₀ является точкой экстремума. Если при этом знак f’(x) меняется.

с «+» на «-», то x₀ - точка максимума,

с «-» на «+», то x₀ - точка минимума.

Доказательство. Пусть f’(x) при переходе x через точку x₀ изменяет знак с «+» на «-», то есть f’(x)>0 при x Î (x₀-; x₀)

и f’(x)<0 при x Î (x₀;x₀ +), где >0.

(рис.10).

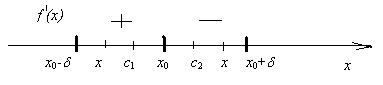
Рис. 10

1) Пусть x Î (x₀-; x₀). На отрезке [x;x₀] функция y = f(x) удовлетворяет теореме Лагранжа (по условию теоремы 4). Значит, на (x;x₀) найдется хотя бы одна точка c₁, в которой выполняется равенство:

f(x) – f(x₀) = f’(c₁)(x–x₀), где c₁(x₀-;x₀).

Так как f’(c₁) > 0 и x-x₀ < 0, то f(x) – f(x₀) < 0

2) Пусть x Î (x₀;x₀ +). На отрезке [x;x₀] функция y = f(x) также удовлетворяет теореме Лагранжа. Значит на (x₀;x) найдется хотя бы одна точка с₂, в которой выполняется равенство:

f(x) – f(x₀) = f’(c₂)(x–x₀), где c₂  (x₀;x₀+).

Так как f’(c₂) < 0 и x-x₀ > 0, то f(x) – f(x₀) < 0

Следовательно, для любого x Î (x₀-d;x₀ +d) выполняется неравенство:

f(x₀) > f(x).

Отсюда следует, что точка x₀ является точкой максимума функции y = f(x).

Аналогично рассматривается случай, когда f’(x) при переходе x через точку x₀ изменяет знак с «+» на «-». При этом точка x₀ является точкой минимума функции.

Теорема доказана.

БИЛЕТ№15

Теорема 6 (достаточное условие точки перегиба).

Если функция y = f(x) дифференцируема в окрестности точки x_0, вторая производная функции f”(x₀) = 0 или не существует и f”(x) меняет свой знак при переходе x через точку x₀, то точка (x₀;f(x₀)) – точка перегиба кривой y = f(x).

Определение 9. Пусть в точке (x₀;f(x₀)) существует касательная. Тогда точка (x₀;f(x₀)), отделяющая выпуклую часть кривой от вогнутой или наоборот называется точкой перегиба графика функции y = f(x).

Теорема 5 (достаточное условие выпуклости или вогнутости кривой).

Пусть функция y = f(x) дважды дифференцируема на промежутке (a;b) и f”(x) для x Î (a;b) сохраняет свой знак, то кривая y = f(x) выпуклая, если f”(x)  0 при x Î (a;b), и кривая y = f(x) вогнутая, если f”(x)  0 при x Î (a;b).

4. Выпуклость, вогнутость и точки перегиба графика функции

Пусть функция y = f(x) дифференцируема в любой точке промежутка (a;b). Тогда она имеет конечную производную в любой точке этого промежутка. Значит, существует касательная к графику функции y = f(x) в любой его точке (x;f(x)), a < x < b.

Определение 8. График функции y = f(x), дифференцируемой в каждой точке промежутка (a;b) называется выпуклым (вогнутым) на этом промежутке, если для любого x Î (a;b) график расположен не выше (не ниже) касательной к графику в точке (x;f(x)).

БИЛЕТ№16

1. Асимптоты плоской кривой

Определение 1. Если точка M(x;y) перемещается по кривой y = f(x) так, что хотя бы одна из координат точки стремиться к  и при этом расстояние от этой точки до некоторой прямой стремиться к 0, то эта прямая называется асимптотой кривой y = f(x).

Асимптоты бывают двух видов: вертикальные и наклонные.

Теорема 1. Для того чтобы кривая y = f(x) имела наклонную асимптоту при x®+¥ (или x®-¥) необходимо и достаточно существования двух конечных пределов:

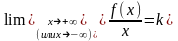и

Доказательство. Ограничимся случаем x®+¥.

Необходимость. Пусть y = kx+b – наклонная асимптота при x®+¥ кривой y = f(x). Тогда функция f(x) представима в виде:

, где при .

Убедимся в существовании конечных пределов:

.

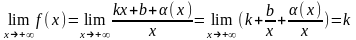необходимость доказана.

Достаточность. Пусть существуют конечные пределы и .

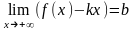Тогда по свойству конечных пределов второй предел можно переписать в виде:

, где (x) – бесконечно малая при x®+¥.

Отсюда получаем:

, где при .

Достаточность доказана.

БИЛЕТ№17

Теорема 1 (об общем виде первообразной).

Пусть F(x) – одна из первообразных для функции f(x) на интервале (a;b). Тогда любая другая первообразная для f(x) на (a;b) представима в виде

F(x)+C, где C – некоторое число.

Доказательство. Во-первых, проверим, что F(x)+C, где С – некоторое число, также является первообразной для f(x) на (a;b).

По условию теоремы F(x) на (a;b) является первообразной для f(x), поэтому выполняется равенство:

F’(x) = f(x) при любом xÎ (a;b).

Так как С – некоторое число, то

(F(x)+С)’ = F’(x)+С’ = F’(x)+0 = f(x).

Отсюда следует: (F(x)+С)’ = f(x) при любом xÎ (a;b), а значит F(x)+С на (a;b) является первообразной для f(x).

Во-вторых, проверим, что если F(x) и Ф(x) – две первообразные для функции f(x) на (a;b), то они различаются между собой на постоянную величину, то есть F(x) – Ф(x) = const.

Обозначим (x) = F(x) - Ф(x). Ток как по предположению функции F(x) и Ф(x) первообразные на (a;b) для f(x), то выполняются равенства: F’(x) = f(x) и Ф’(x) = f(x) при любом xÎ (a;b). Следовательно, ’(x) = F’(x)-Ф’(x) = f(x)- f(x) = 0 при любом xÎ (a;b).

Функция (x) непрерывна и дифференцируема при xÎ (a;b). Значит, на любом [x₁;x₂]  (a;b) функция (x) удовлетворяет теореме Лагранжа: существует точка Î (x₁;x₂) для которой выполняется равенство:

(x₂) - (x₁) = ’( ) (x₂-x₁) = 0(x₂-x₁) = 0.

 (x2) - (x1) = 0  (x2) = (x1)  (x) = const.

Значит, F(x) – Ф(x) = const.

Итак, получили, что если известна одна первообразная F(x) для функции f(x) на промежутке (a;b), то любая другая первообразная может быть представлена в виде F(x)+С, где С – постоянная величина. Этот вид первообразных носит название ее общего вида, при этом С –произвольная постоянная величина.

Определение 1. Функция F(x) называется первообразной функции f(x), на некотором промежутке, если в каждой точке этого промежутка функция F(x) дифференцируема и выполняется равенство:

F’(x) = f(x).

БИЛЕТ№18

2. Понятие неопределенного интеграла

Определение 2. Множество всех первообразных данной функции f(x) на интервале (a;b) называется неопределенным интегралом функции f(x) на этом интервале и обозначается символом:

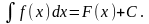
Замечание. Все вышеперечисленные свойства верны при условии. Что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.

3. Свойства неопределенного интеграла.

Из определений первообразной F(x) неопределенного интеграла от данной функции f(x) на некотором промежутке следуют свойства неопределенного интеграла:

1. .

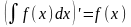2. .

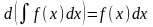3. 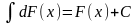, где С – произвольная постоянная.

4. 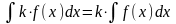, где k = const.

5.

БИЛЕТ№19

2. Интегрирование подстановкой.

Подстановка (или замена переменной) базируется на следующей теореме.

Теорема 1. Если не удается найти интеграл 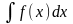непосредственно, то можно выбрать такую функцию x = j(t), удовлетворяющую условиям:

1) j(t) непрерывна при t  (;), соответствующем интервалу xÎ (a;b),

2) дифференцируемая при tÎ (a;b);

3) имеет обратную функцию t = j^-1(x), чтобы

|

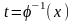
Был табличный или проще. Иногда для упрощения интеграла можно сделать замену t = (x).

Замечание. Выбор правильной подстановки в значительной степени зависит от искусства вычислителя.

Пример 10.

.

Ответ: .

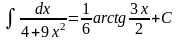БИЛЕТ№20

3. Интегрирование по частям.

Метод интегрирования по частям базируется на следующей теореме:

Теорема 2. Пусть функция U = U(x) и V = V(x) дифференцируемы на некотором интервале (a;b). Пусть на (a;b) функция V(x)U’(x) имеет первообразную. Тогда на (a;b) функция U(x)V’(x) также имеет первообразную. При этом справедливо равенство:

.

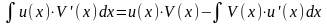Доказательство. По форме дифференцирования:

(U(x)V(x))’ = U’(x)V(x) + U(x)V’(x).

По свойству неопределенного интеграла:

.

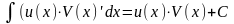Тогда можно записать:

БИЛЕТ№21

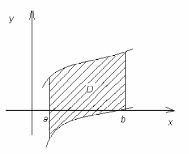
2. Геометрический смысл определенного интеграла

1)

.

2) Если область ограничена двумя кривыми y = f (x) и y = g (x), причем при x [a;b] f (x)  g (x), то площадь области ограниченным кривыми y = f (x); y = g (x) и прямыми x = a, x = b вычисляется по формуле: