
- •3. Точки разрыва функции и их классификация
- •4. Правила дифференцирования
- •3. Дифференцируемость функции.
- •2. Монотонность функции
- •§ 8. Определенный интеграл.
- •2) Формула Ньютона-Лейбница
- •1. Частные производные функции нескольких переменных
- •Дифференцируемость функции двух переменных
- •Частные производные и дифференциалы высших порядков.
- •Дифференциал функции двух переменных
- •1. Производная по направлению.
- •Экстремумы функций двух и трех переменных
Вопрос №1
Определение
4. Число А называется пределом
функции
f(x)
при
x
x0,
если для любого наперед заданного малого
числа ε > 0 существует такое малое число
 ,
что для любого x,
принадлежащего
D(f)
и проколотой δ-окрестности точки x0,
то есть
,
что для любого x,
принадлежащего
D(f)
и проколотой δ-окрестности точки x0,
то есть
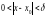 ,
выполняется неравенство:
,
выполняется неравенство:
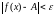 .
.
Итак:

 и
и
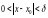

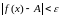 .
.
Бесконечно малые и бесконечно большие функции
Определение
8. Функция (x)
называется бесконечно
малой при x
x0,
или в точке
 ,
если
предел (x)
при x
,
равен нулю:
,
если
предел (x)
при x
,
равен нулю:
 .
.
Основные свойства бесконечно малых функций
1)
Алгебраическая сумма конечного числа
бесконечно малых функций в точке
есть бесконечно малая функция в этой
точке
.
То есть: если
 - бесконечно малые функции в точке
,
то
- бесконечно малые функции в точке
,
то
 - бесконечно малая функция в этой точке
.
- бесконечно малая функция в этой точке
.
2)
Произведение конечного числа бесконечно
малых функций в точке
есть
бесконечно малая функция в точке
.
То есть: если
- бесконечно малые функции в точке
,
то
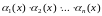 - бесконечно малая функция в этой точке
.
- бесконечно малая функция в этой точке
.
3) Произведение бесконечно малой функции в точке на ограниченную функцию в некоторой окрестности точки есть бесконечно малая функция в точке , то есть, если α(x) бесконечно малая функция в точке и f(x) ограниченная в некоторой окрестности точки , то α(x)f(x) – бесконечно малая функция в точке .
ВОПРОС№2
Теорема 2. Если существуют конечные пределы двух функций f(x) и g(x) в точке , то существует конечный предел суммы этих функций в точке , равный сумме пределов этих функций.
Доказательство:
Пусть
 ,
тогда по теореме 1 f(x)=А+a(x),
где a(x)–
бесконечно малая функция в точке x0.
,
тогда по теореме 1 f(x)=А+a(x),
где a(x)–
бесконечно малая функция в точке x0.
Пусть,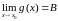 ,
тогда по теореме 1 g(x)=B+β(x),
где β(x)
– бесконечно малая функция в точке x0.
Рассмотрим сумму этих функций: f(x)
+ g(x)
= = A
+
a(x)
+B
+
β(x)
= (A+B)
+
a(x)
+ β(x),
обозначим γ(x)
= a(x)
+
β(x)
-
,
тогда по теореме 1 g(x)=B+β(x),
где β(x)
– бесконечно малая функция в точке x0.
Рассмотрим сумму этих функций: f(x)
+ g(x)
= = A
+
a(x)
+B
+
β(x)
= (A+B)
+
a(x)
+ β(x),
обозначим γ(x)
= a(x)
+
β(x)
-
бесконечно малая функция в точке x0 (по свойству 1 бесконечно малых функций). Получим f(x)+g(x)=A+B+γ(x).
По
теореме 1:

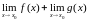 .
.
Теорема доказана.
Теорема 3. Если существуют конечные пределы двух функций f(x) и g(x) в точке , то существует предел произведения этих функций в точке , равный произведению пределов этих функций.
Доказательство:
Пусть =А,
тогда по теореме 1: f(x)=А+a(x),
где a(x)
–
бесконечно малая функция в точке
.
Пусть
=А,
тогда по теореме 1: f(x)=А+a(x),
где a(x)
–
бесконечно малая функция в точке
.
Пусть
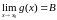 ,
тогда по теореме 1: g(x)
= B
+ β(x),
где β(x)
– бесконечно малая функция в точке
.
Рассмотрим произведение этих функций:
,
тогда по теореме 1: g(x)
= B
+ β(x),
где β(x)
– бесконечно малая функция в точке
.
Рассмотрим произведение этих функций:
f(x) × g(x) = (А +a(x))(B + β(x)) = AB + B×a(x) + A×β(x) + a(x) ×β(x).
Обозначим: Ba(x) + Aβ(x) + a(x)β(x) = γ(x) – бесконечно малая функция в точке (по свойствам бесконечно малых функций). Получим: f(x)×g(x) = A×B + γ(x).
По
теореме 1:
 .
.
Теорема доказана.
Теорема
4. Если существуют конечные пределы f(x)
и g(x),
причем
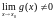 ,
то существует предел частного этих
функций
,
то существует предел частного этих
функций
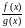 в точке
,
равный частному пределов этих функций.
в точке
,
равный частному пределов этих функций.
То
есть: если существует
 =А
и существует
=А
и существует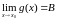 ,
B≠0,
то существует
,
B≠0,
то существует
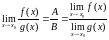 .
.
ВОПРОС№3
6. Первый замечательный предел
Теорема
6. Предел функции
 в точке x
=
0 существует и равен 1, то есть:
в точке x
=
0 существует и равен 1, то есть:
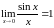 .
.
Доказательство:
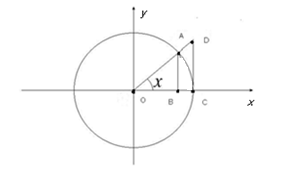
Пусть x > 0 (x
 )
)
 (1)
(1)
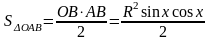 ;
;
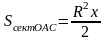 ;
;
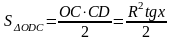
(x – в радианах)
Подставим в соотношение (1) полученные значения площадей:
 ,
,
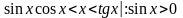 ,
,
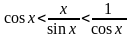
Так как все части двойного неравенства положительные, можно переписать так:

Т.к.
 то по теореме 5:
то по теореме 5:
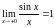 .
.
Пусть x<0 (x
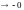 )
)
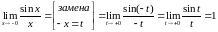 (по
доказанному в первом случае)
(по
доказанному в первом случае)
Следовательно,
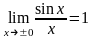 .
.
Теорема доказана.
7. Второй замечательный предел
Теорема
7. Предел функции
 при x
при x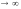 существует
и равен числу e,
то есть:
существует
и равен числу e,
то есть:
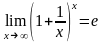 .
.
БИЛЕТ№4
1. Непрерывность функции в точке и на промежутке
Определение 1. Функция f(x) называется непрерывной в точке x0D(f), если она определена в некоторой окрестности точки x0 и предел f(x) в точке x0 равен значению функции в этой точке, то есть:
 =
= .
.
Определение
2. Функция f(x)
называется непрерывной в точке x0D(f),
если она определена в некоторой
окрестности этой точки и бесконечно
малому приращению аргумента
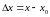 соответствует бесконечно малое приращение
функции
соответствует бесконечно малое приращение
функции
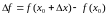 ,
то есть:
,
то есть:
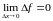 .
.
Определение 3. Функция f(x) называется непрерывной в точке x0D(f), если она определена в некоторой окрестности этой точки и существует правый и левый предел f(x) в точке , причем они равны между собой и равны значению функции в этой точке, то есть:
а) = А;
= А;
б)
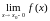 = В;
= В;
в)
А
=
В
= .
.
Определение 4. Функция f(x) называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.
3. Точки разрыва функции и их классификация
Определение 5. Точка x0 называется точкой разрыва функции f(x), если в этой точке функция либо не определена, либо определена, но нарушено хотя бы одно из условий определения 3 непрерывности f(x).
Классификация точек разрыва
Определение 6. Точка x0 называется точкой устранимого разрыва функции f(x), если предел функции в этой точке существует, но f(x) в точке x0 либо не определена, либо имеет значение f(x0), не совпадающее с найденным пределом:
f(x0-0)= f(x0+0) ¹ f(x0).
Определение 7. Точка x0 называется точкой разрыва первого рода функции f(x) (разрыв типа «скачка»), если в этой точке функция имеет конечные, но не равные между собой правый и левый пределы, то есть:
f(x0-0) ¹f(x0+0).
Определение 8. Точка x0 называется точкой разрыва второго рода функции f(x), если в этой точке f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Примеры. Исследовать функции на непрерывность и точки разрыва.
1.
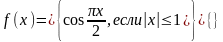
Решение.
На промежутке (-∞;-1) f(x)=
-x+1,
на (-1;1)
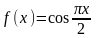 и на (1;+∞) f(x)
= x-1.
и на (1;+∞) f(x)
= x-1.
БИЛЕТ№5
Определение
2. Производной
функции
y
= f(x)
называется предел отношения приращения
функции Dy
к приращению аргумента Dx,
если приращение аргумента Dx
стремится к нулю и этот предел существует.
Производную функции y
=
f(x)
обозначают:
 или
или
 .
Поэтому можно записать:
.
Поэтому можно записать:

Геометрический смысл производной
Рассмотрим график функции y = f(x) в окрестности фиксированной точки x0 (рис.5).

Рис. 5
Точка M0(x0;y(x0)) – фиксированная точка графика y = f(x). Точка M(x0+Dx;y(x0+Dx)) при различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx 0), то секущая линия M0M стремится к своему предельному положению, называемому касательной к линии y = f(x) в точке M0.
Рассмотрим
M0MA:
tgсек=
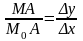 ,
сек
= угол наклона секущей M0M
к оси Ox.
,
сек
= угол наклона секущей M0M
к оси Ox.
Перейдем к пределу при Dx 0:
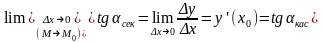
То есть y' (x0) = tg кас => частное значение производной функции y = f(x) в точке x0 равно угловому коэффициенту касательной, проведенной к линии y = f(x) в точке M0(x0;y(x0)).
Тогда, используя уравнение прямой, проходящей через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y = f(x) в точке M0(x0;f(x0)):
y = f(x0) + f' '(x0) × (x-x0)
Аналогично, можно записать уравнение нормали – прямой, перпендикулярной касательной и проходящей через точку касания M0(x0;f(x0)):
y
=
f(x0)
-
 ,
,
используя
условие перпендикулярности прямых:
Kнорм
= - .
.
БИЛЕТ№6
4. Правила дифференцирования
Теорема 3. Если функции U(x) и V(x) дифференцируемы в точке x, то функция U(x) V(x) дифференцируема в т.x и ее производная вычисляется по формуле:
(U(x) V(x))' = (U(x))' (V(x))'.
Доказательство: Рассмотрим функцию y = U(x) V(x).
Тогда y=UV. Разделим на x и перейдем к пределу при x0:

так как по условию теоремы функции U(x) и V(x) дифференцируемы.
Значит, (U(x) V(x))' = U' (x) V' (x).
Теорема доказана.
Теорема 4. Если функции U(x) и V(x) дифференцируемы в т. х, то функция (U(x) V(x)) дифференцируема в т. х и ее производная вычисляется по формуле:
(U(x) V(x))' = (U(x))' V(x) + U(x) (V(x))'.
Доказательство. Рассмотрим функцию y = U(x)V(x). Найдем ее приращение y = (U+U)(V+V) - UV = UV + UV + VDU + DUDV -UV= = UDV + VDU + DUDV.
Разделим Dy на Dx и перейдем к пределу при Dx0:

так
по условию функции U(x)
и V(x)
дифференцируемы, а значит
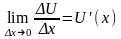 ,
,
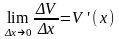 и
и
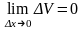 .
.
Значит, (U(x) V(x))' = U’(x) V(x) + U(x) V' (x).
Теорема доказана.
Следствия.
а) Если U(x), V(x) и W(x) дифференцируемы в т. х, то функция (U(x) V(x) W(x)) дифференцируема в т. х и ее производная вычисляется по формуле:
(UV×W)' = U'×V×W + U×V'×W + U×V×W'.
б) Производная постоянной, умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на производную функции:
(C×U(x))' = C×U' (x).
Теорема
5. Если функции U(x)
и V(x)
дифференцируемы в точке х
и V(x)0,
то функция
 дифференцируема в точке х
и ее производная вычисляется по формуле:
дифференцируема в точке х
и ее производная вычисляется по формуле:
 .
.
Доказательство.
Рассмотрим функцию
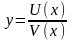 .
Найдем ее приращение
.
Найдем ее приращение
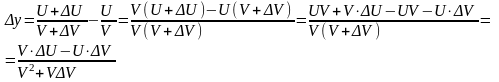
Разделим y на x и перейдем к пределу при x0:

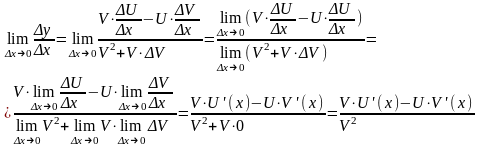
Значит,
 .
.
Теорема доказана.
Теорема 6 (производная сложной функции)
Если функция f(u) дифференцируема в точке u, а функция u(x) дифференцируема в точке x, причем u = u(x), тогда сложная функция f(u(x)) дифференцируема в точке x и ее производная вычисляется по формуле:
(f (u(x)))' = f '(u) ×u' (x).
Доказательство. Рассмотрим функцию y = f(U). Так как функция f(u) дифференцируема в точке u, то ее приращение можно записать в виде:
 ,
где
,
где
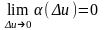
Разделим на Dx и перейдем к пределу при Dx0:
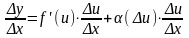
 (если
Dx0,
то Du0,
т.к. u(x)
дифференцируема, а значит непрерывна)
(если
Dx0,
то Du0,
т.к. u(x)
дифференцируема, а значит непрерывна)
Значит: (f(u(x)))' = f’(u) ×u' (x).
Теорема доказана.
БИЛЕТ№7
